10.4.
The Pendulum
As Figure 10.22 shows, a simple pendulum consists of a particle of mass m, attached to a frictionless pivot P by a cable of length L and negligible mass. When the particle is pulled away from its equilibrium position by an angle q and released, it swings back and forth. By attaching a pen to the bottom of the swinging particle and moving a strip of paper beneath it at a steady rate, we can record the position of the particle as time passes. The graphical record reveals a pattern that is similar (but not identical) to the sinusoidal pattern for simple harmonic motion.
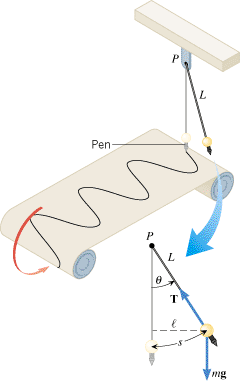 | | Figure 10.22
A simple pendulum swinging back and forth about the pivot P. If the angle
q
is small, the swinging is approximately simple harmonic motion. |
|
The force of gravity is responsible for the back-and-forth rotation about the axis at P. The rotation speeds up as the particle approaches the lowest point on the arc and slows down on the upward part of the swing. Eventually the angular speed is reduced to zero, and the particle swings back. As Section 9.4 discusses, a net torque is required to change the angular speed. The gravitational force mg produces this torque. (The tension T in the cable creates no torque, because it points directly at the pivot P and, therefore, has a zero lever arm.) According to Equation 9.1, the magnitude of the torque t is the product of the magnitude mg of the gravitational force and the lever arm 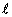 , so that t
, so that t =
= – (mg)
– (mg)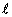 . The minus sign is included since the torque is a restoring torque: that is, it acts to reduce the angle q [the angle q is positive (counterclockwise), while the torque is negative (clockwise)]. The lever arm
. The minus sign is included since the torque is a restoring torque: that is, it acts to reduce the angle q [the angle q is positive (counterclockwise), while the torque is negative (clockwise)]. The lever arm 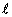 is the perpendicular distance between the line of action of mg and the pivot P. From Figure 10.22 it can be seen that
is the perpendicular distance between the line of action of mg and the pivot P. From Figure 10.22 it can be seen that 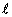 is very nearly equal to the arc length s of the circular path when the angle q is small (about 10° or less). Furthermore, if q is expressed in radians, the arc length and the radius L of the circular path are related, according to s
is very nearly equal to the arc length s of the circular path when the angle q is small (about 10° or less). Furthermore, if q is expressed in radians, the arc length and the radius L of the circular path are related, according to s =
= Lq (Equation 8.1). Under these conditions, it follows that
Lq (Equation 8.1). Under these conditions, it follows that 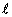

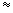
 s
s =
= Lq , and the torque created by gravity is
Lq , and the torque created by gravity is
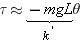 |  |
In the equation above, the term mgL has a constant value k', independent of q . For small angles, then, the torque that restores the pendulum to its vertical equilibrium position is proportional to the angular displacement q . The expression t =
= –k'q has the same form as the Hooke’s law restoring force for an ideal spring, F
–k'q has the same form as the Hooke’s law restoring force for an ideal spring, F =
= –kx. Therefore, we expect the frequency of the back-and-forth movement of the pendulum to be given by an equation analogous to Equation 10.11
–kx. Therefore, we expect the frequency of the back-and-forth movement of the pendulum to be given by an equation analogous to Equation 10.11 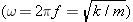 . In place of the spring constant k, the constant k'
. In place of the spring constant k, the constant k' =
= mgL will appear, and, as usual in rotational motion, in place of the mass m, the moment of inertia I will appear:
mgL will appear, and, as usual in rotational motion, in place of the mass m, the moment of inertia I will appear:
 | (10.15) |  |
The moment of inertia of a particle of mass m, rotating at a radius r =
= L about an axis, is given by I
L about an axis, is given by I =
= mL2 (Equation 9.6). Substituting this expression for I into Equation 10.15 reveals for a simple pendulum that
mL2 (Equation 9.6). Substituting this expression for I into Equation 10.15 reveals for a simple pendulum that
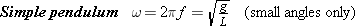 | (10.16) |  |
The mass of the particle has been eliminated algebraically from this expression, so only the length L and the acceleration g due to gravity determine the frequency of a simple pendulum. If the angle of oscillation is large, the pendulum does not exhibit simple harmonic motion, and Equation 10.16 does not apply. Equation 10.16 provides the basis for using a pendulum to keep time, as Example 10 demonstrates.
 Concept Simulation 10.2 Concept Simulation 10.2 |
 |
This simulation allows you to see the pendulum motion in Figure 10.22. A plot of the angular displacement versus time is synchronized with the motion, and, among other things, you can explore the effects of changing the length of the pendulum and the acceleration due to gravity. Related Homework: Conceptual Questions 11, 12, Problem 41 |
|
 |
 |
|
Determine the length of a simple pendulum that will swing back and forth in simple harmonic motion with a period of 1.00 s.
Reasoning
When a simple pendulum is swinging back and forth in simple harmonic motion, its frequency f is given by Equation 10.16 as  , where g is the acceleration due to gravity and L is the length of the pendulum. We also know from Equation 10.5 that the frequency is the reciprocal of the period T, so , where g is the acceleration due to gravity and L is the length of the pendulum. We also know from Equation 10.5 that the frequency is the reciprocal of the period T, so 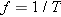 . Thus, the equation above becomes . Thus, the equation above becomes 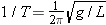 . We can solve this equation for the length L of the pendulum. . We can solve this equation for the length L of the pendulum.
Solution
The length of the pendulum is
Figure 10.23 shows a clock that uses a pendulum to keep time.
 | | Figure 10.23
This pendulum clock keeps time as the pendulum swings back and forth. (© Robert Mathena/ Fundamental Photographs) |
|
|
 |
It is not necessary that the object in Figure 10.22 be a particle. It may be an extended object, in which case the pendulum is called a physical pendulum. For small oscillations, Equation 10.15 still applies, but the moment of inertia I is no longer mL2. The proper value for the rigid object must be used. (See Section 9.4 for a discussion of moment of inertia.) In addition, the length L for a physical pendulum is the distance between the axis at P and the center of gravity of the object. The next example deals with an important type of physical pendulum.
| Example 11 Pendulum Motion and Walking |
 |
| Copyright © 2000-2003 by John Wiley & Sons, Inc. or related companies. All rights reserved. |


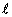 , so that t
, so that t![]() =
=![]() – (mg)
– (mg)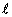 . The minus sign is included since the torque is a restoring torque: that is, it acts to reduce the angle q [the angle q is positive (counterclockwise), while the torque is negative (clockwise)]. The lever arm
. The minus sign is included since the torque is a restoring torque: that is, it acts to reduce the angle q [the angle q is positive (counterclockwise), while the torque is negative (clockwise)]. The lever arm 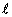 is the perpendicular distance between the line of action of mg and the pivot P. From Figure 10.22 it can be seen that
is the perpendicular distance between the line of action of mg and the pivot P. From Figure 10.22 it can be seen that 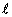 is very nearly equal to the arc length s of the circular path when the angle q is small (about 10° or less). Furthermore, if q is expressed in radians, the arc length and the radius L of the circular path are related, according to s
is very nearly equal to the arc length s of the circular path when the angle q is small (about 10° or less). Furthermore, if q is expressed in radians, the arc length and the radius L of the circular path are related, according to s![]() =
=![]() Lq (Equation 8.1). Under these conditions, it follows that
Lq (Equation 8.1). Under these conditions, it follows that 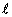
![]()
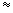
![]() s
s![]() =
=![]() Lq , and the torque created by gravity is
Lq , and the torque created by gravity is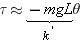
![]() =
=![]() –k'q has the same form as the Hooke’s law restoring force for an ideal spring, F
–k'q has the same form as the Hooke’s law restoring force for an ideal spring, F![]() =
=![]() –kx. Therefore, we expect the frequency of the back-and-forth movement of the pendulum to be given by an equation analogous to Equation 10.11
–kx. Therefore, we expect the frequency of the back-and-forth movement of the pendulum to be given by an equation analogous to Equation 10.11 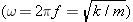 . In place of the spring constant k, the constant k'
. In place of the spring constant k, the constant k'![]() =
=![]() mgL will appear, and, as usual in rotational motion, in place of the mass m, the moment of inertia I will appear:
mgL will appear, and, as usual in rotational motion, in place of the mass m, the moment of inertia I will appear:
![]() =
=![]() L about an axis, is given by I
L about an axis, is given by I![]() =
=![]() mL2 (Equation 9.6). Substituting this expression for I into Equation 10.15 reveals for a simple pendulum that
mL2 (Equation 9.6). Substituting this expression for I into Equation 10.15 reveals for a simple pendulum that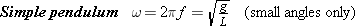
 Concept Simulation 10.2
Concept Simulation 10.2 of the thin rod into this result gives
of the thin rod into this result gives
 .
.