10.5. Damped Harmonic Motion

In simple harmonic motion, an object oscillates with a constant amplitude, because there is no mechanism for dissipating energy. In reality, however, friction or some other energy-dissipating mechanism is always present. In the presence of energy dissipation, the amplitude of oscillation decreases as time passes, and the motion is no longer simple harmonic motion. Instead, it is referred to as damped harmonic motion, the decrease in amplitude being called “damping.”

One widely used application of damped harmonic motion is in the suspension system of an automobile. Figure 10.24a shows a shock absorber attached to a main suspension spring of a car. A shock absorber is designed to introduce damping forces, which reduce the vibrations associated with a bumpy ride. As part b of the drawing shows, a shock absorber consists of a piston in a reservoir of oil. When the piston moves in response to a bump in the road, holes in the piston head permit the piston to pass through the oil. Viscous forces that arise during this movement cause the damping.

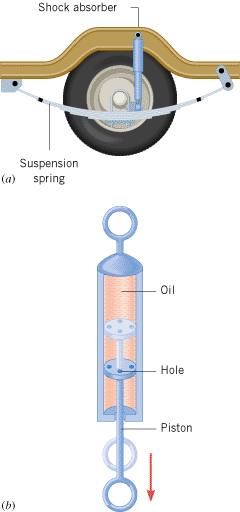Figure 10.24 (a) A shock absorber mounted in the suspension system of an automobile and (b) a simplified, cutaway view of the shock absorber.

Figure 10.25 illustrates the different degrees of damping that can exist. As applied to the example of a car’s suspension system, these graphs show the vertical position of the chassis after it has been pulled upward by an amount A₀ at time t₀=0 s and then released. Part a of the figure compares undamped or simple harmonic motion in curve 1 (red) to slightly damped motion in curve 2 (green). In damped harmonic motion, the chassis oscillates with decreasing amplitude and it eventually comes to rest. As the degree of damping is increased from curve 2 to curve 3 (gold), the car makes fewer oscillations before coming to a halt. Part b of the drawing shows that as the degree of damping is increased further, there comes a point when the car does not oscillate at all after it is released but, rather, settles directly back to its equilibrium position, as in curve 4 (blue). The smallest degree of damping that completely eliminates the oscillations is termed “critical damping,” and the motion is said to be critically damped.

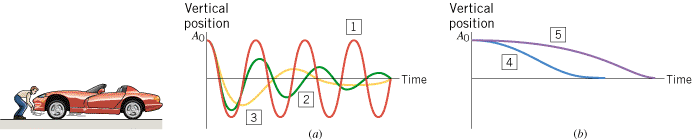Damped harmonic motion. The degree of damping increases from curve 1 to curve 5. Curve 1 represents undamped or simple harmonic motion. Curves 2 and 3 show underdamped motion. Curve 4 represents critically damped harmonic motion. Curve 5 shows overdamped motion.

Figure 10.25 Damped harmonic motion. The degree of damping increases from curve 1 to curve 5. Curve 1 represents undamped or simple harmonic motion. Curves 2 and 3 show underdamped motion. Curve 4 represents critically damped harmonic motion. Curve 5 shows overdamped motion.

Figure 10.25b also shows that the car takes the longest time to return to its equilibrium position in curve 5 (purple), where the degree of damping is above the value for critical damping. When the damping exceeds the critical value, the motion is said to be overdamped. In contrast, when the damping is less than the critical level, the motion is said to be underdamped (curves 2 and 3). Typical automobile shock absorbers are designed to produce underdamped motion somewhat like that in curve 3.

Concept Simulation 10.3

Here, simple harmonic motion is compared to damped harmonic motion. For an object on a spring you can adjust the spring constant, the mass and initial position of the object, and the extent of the damping. Graphs of the object’s position, velocity, and acceleration versus time are synchronized with the motion and allow you to see the effects of your adjustments.

Related Homework: Problem 17, 68