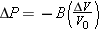10.7.
Elastic Deformation
STRETCHING, COMPRESSION, AND YOUNG’S MODULUS
We have seen that a spring returns to its original shape when the force compressing or stretching it is removed. In fact, all materials become distorted in some way when they are squeezed or stretched, and many of them, such as rubber, return to their original shape when the squeezing or stretching is removed. Such materials are said to be “elastic.” From an atomic viewpoint, elastic behavior has its origin in the forces that atoms exert on each other, and Figure 10.28 symbolizes these forces with the aid of springs. It is because of these atomic-level “springs” that a material tends to return to its initial shape once the forces that cause the deformation are removed.
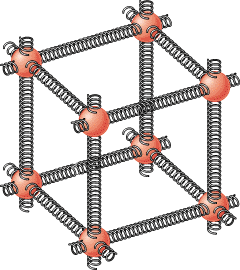 | | Figure 10.28
The forces between atoms act like springs. The atoms are represented by red spheres, and the springs between some atoms have been omitted for clarity. |
|
The interatomic forces that hold the atoms of a solid together are particularly strong, so considerable force must be applied to stretch a solid object. Experiments have shown that the magnitude of the force can be expressed by the following relation, provided that the amount of stretching is small compared to the original length of the object:
 | (10.17) |  |
As Figure 10.29 shows, F denotes the magnitude of the stretching force applied perpendicularly to the surface at the end, A is the cross-sectional area of the rod, DL is the increase in length, and L0 is the original length. The term Y is a proportionality constant called Young’s modulus, after Thomas Young (1773–1829). Solving Equation 10.17 for Y shows that Young’s modulus has units of force per unit area (N/m2). It should be noted that the magnitude of the force in Equation 10.17 is proportional to the fractional increase in length DL/L0, rather than the absolute increase DL. The magnitude of the force is also proportional to the cross-sectional area A, which need not be circular, but can have any shape (e.g., rectangular).
 | | Figure 10.29
In this diagram, F denotes the stretching force, A the cross-sectional area, L0 the original length of the rod, and DL the amount of stretch. |
|
Table 10.1 reveals that the value of Young’s modulus depends on the nature of the material. The values for metals are much larger than those for bone, for example. Equation 10.17 indicates that, for a given force, the material with the greater value of Y undergoes the smaller change in length. This difference between the changes in length is the reason why surgical implants (e.g., artificial hip joints), which are often made from stainless steel or titanium alloys, can lead to chronic deterioration of the bone that is in contact with the implanted prosthesis.
| Table 10.1
Values for the Youngs Modulus of Solid Materials |
|
Material
|
Young’s Modulus Y (N/m2)
| |
Aluminum
|
6.9 × × 1010 1010
|
Bone
|
Compression
|
9.4 × × 109 109
|
Tension
|
1.6 × × 1010 1010
|
Brass
|
9.0 × × 1010 1010
|
Brick
|
1.4 × × 1010 1010
|
Copper
|
1.1 × × 1011 1011
|
Mohair
|
2.9 × × 109 109
|
Nylon
|
3.7 × × 109 109
|
Pyrex glass
|
6.2 × × 1010 1010
|
Steel
|
2.0 × × 1011 1011
|
Teflon
|
3.7 × × 108 108
|
Titanium
|
1.2 × × 1011 1011
|
Tungsten
|
3.6 × × 1011 1011
|
|
|
Forces that are applied as in Figure 10.29 and cause stretching are called “tensile” forces, because they create a tension in the material, much like the tension in a rope. Equation 10.17 also applies when the force compresses the material along its length. In this situation, the force is applied in a direction opposite to that shown in Figure 10.29, and DL stands for the amount by which the original length L0 decreases. Table 10.1 indicates, for example, that bone has different values of Young’s modulus for compression and tension, the value for tension being greater. Such differences are related to the structure of the material. The solid part of bone consists of collagen fibers (a protein material) distributed throughout hydroxyapatite (a mineral). The collagen acts like the steel rods in reinforced concrete and increases the value of Y for tension relative to that for compression.
Most solids have Young’s moduli that are rather large, reflecting the fact that a large force is needed to change the length of a solid object by even a small amount, as Example 12 illustrates.
| Example 12 Bone Compression |
SHEAR DEFORMATION AND THE SHEAR MODULUS
It is possible to deform a solid object in a way other than stretching or compressing it. For instance, place a book on a rough table and push on the top cover, as in Figure 10.31a. Notice that the top cover, and the pages below it, become shifted relative to the stationary bottom cover. The resulting deformation is called a shear deformation and occurs because of the combined effect of the force F applied (by the hand) to the top of the book and the force –F applied (by the table) to the bottom of the book. The directions of the forces are parallel to the covers of the book, each of which has an area A, as illustrated in part b of the drawing. These two forces have equal magnitudes, but opposite directions, so the book remains in equilibrium. Equation 10.18 gives the magnitude F of the force needed to produce an amount of shear DX for an object with thickness L0:
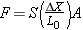 | (10.18) |  |
This equation is very similar to Equation 10.17. The constant of proportionality S is called the shear modulus and, like Young’s modulus, has units of force per unit area (N/m2). The value of S depends on the nature of the material, and Table 10.2 gives some representative values. Example 13 illustrates how to determine the shear modulus of a favorite dessert.
 | | Figure 10.31
(a) An example of a shear deformation. The shearing forces F and –
F are applied parallel to the top and bottom covers of the book. In general, shearing forces cause a solid object to change its shape. (b) The shear deformation is D
X. The area of each cover is A, and the thickness of the book is L0. |
|
| Table 10.2
Values for the Shear Modulus of Solid Materials |
|
Material
|
Shear Modulus S (N/m2)
| |
Aluminum
|
2.4 × × 1010 1010
|
Bone
|
1.2 × × 1010 1010
|
Brass
|
3.5 × × 1010 1010
|
Copper
|
4.2 × × 1010 1010
|
Lead
|
5.4 × × 1010 1010
|
Nickel
|
7.3 × × 1010 1010
|
Steel
|
8.1 × × 1010 1010
|
Tungsten
|
1.5 × × 1011 1011
|
|
|
Although Equations 10.17 and 10.18 are algebraically similar, they refer to different kinds of deformations. The tensile force in Figure 10.29 is perpendicular to the surface whose area is A, whereas the shearing force in Figure 10.31 is parallel to that surface. Furthermore, the ratio DL/L0 in Equation 10.17 is different from the ratio DX/L0 in Equation 10.18. The distances DL and L0 are parallel, whereas DX and L0 are perpendicular. Young’s modulus refers to a change in length of one dimension of a solid object as a result of tensile or compressive forces. The shear modulus refers to a change in shape of a solid object as a result of shearing forces.
VOLUME DEFORMATION AND THE BULK MODULUS
When a compressive force is applied along one dimension of a solid, the length of that dimension decreases. It is also possible to apply compressive forces so that the size of every dimension (length, width, and depth) decreases, leading to a decrease in volume, as Figure 10.33 illustrates. This kind of overall compression occurs, for example, when an object is submerged in a liquid, and the liquid presses inward everywhere on the object. The forces acting in such situations are applied perpendicular to every surface, and it is more convenient to speak of the perpendicular force per unit area, rather than the amount of any one force in particular. The magnitude of the perpendicular force per unit area is called the pressure P.
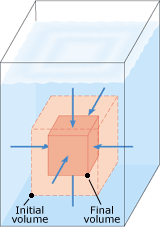 | | Figure 10.33
The arrows denote the forces that push perpendicularly on every surface of an object immersed in a liquid. The force per unit area is the pressure. When the pressure increases, the volume of the object decreases. |
|
Equation 10.19 indicates that the SI unit for pressure is the unit of force divided by the unit of area, or newton/meter2 (N/m2). This unit of pressure is often referred to as a pascal (Pa), named after the French scientist Blaise Pascal (1623–1662).
Suppose we change the pressure on an object by an amount DP, where, as usual, the “delta” notation DP represents the final pressure P minus the initial pressure P0: DP =
= P
P –
– P0. Because of this change in pressure, the volume of the object changes by an amount DV
P0. Because of this change in pressure, the volume of the object changes by an amount DV =
= V
V –
– V0, where V and V0 are the final and initial volumes, respectively. Such a pressure change occurs, for example, when a swimmer dives deeper into the water. Experiment reveals that the change DP in pressure needed to change the volume by an amount DV is directly proportional to the fractional change DV/V0 in the volume:
V0, where V and V0 are the final and initial volumes, respectively. Such a pressure change occurs, for example, when a swimmer dives deeper into the water. Experiment reveals that the change DP in pressure needed to change the volume by an amount DV is directly proportional to the fractional change DV/V0 in the volume:
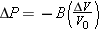 | (10.20) |  |
This relation is analogous to Equations 10.17 and 10.18, except that the area A in those equations does not appear here explicitly; the area is already taken into account by the concept of pressure (force per unit area). The proportionality constant B is known as the bulk modulus. The minus sign occurs because an increase in pressure (DP positive) always creates a decrease in volume (DV negative), and B is given as a positive quantity. Like Young’s modulus and the shear modulus, the bulk modulus has units of force per unit area (N/m2), and its value depends on the nature of the material. Table 10.3 gives representative values of the bulk modulus.
| Table 10.3
Values for the Bulk Modulus of Solid Materials |
|
Material
|
Bulk Modulus B (N/m2)
| |
Solids
|
|
Aluminum
|
7.1 × × 1010 1010
|
Brass
|
6.7 × × 1010 1010
|
Copper
|
1.3 × × 1011 1011
|
Lead
|
4.2 × × 1010 1010
|
Nylon
|
6.1 × × 109 109
|
Pyrex glass
|
2.6 × × 1010 1010
|
Steel
|
1.4 × × 1011 1011
|
Liquids
|
|
Ethanol
|
8.9 × × 108 108
|
oil
|
1.7 × × 109 109
|
water
|
2.2 × × 109 109
|
|
|
| Check Your Understanding 4 |
 |
|
Two rods are made from the same material. One has a circular cross section, and the other has a square cross section. The circle just fits within the square. When the same force is applied to stretch these rods, they each stretch by the same amount. Which rod is longer, or are they equal in length?
Background:
Elastic deformation and Young’s modulus hold the key to this question.
For similar questions (including calculational counterparts), consult Self-Assessment Test 10.2. This test is described at the end of Section 10.8.
|
|
 |
 |
| Copyright © 2000-2003 by John Wiley & Sons, Inc. or related companies. All rights reserved. |




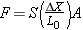


![]() =
=![]() P
P![]() –
–![]() P0. Because of this change in pressure, the volume of the object changes by an amount DV
P0. Because of this change in pressure, the volume of the object changes by an amount DV![]() =
=![]() V
V![]() –
–![]() V0, where V and V0 are the final and initial volumes, respectively. Such a pressure change occurs, for example, when a swimmer dives deeper into the water. Experiment reveals that the change DP in pressure needed to change the volume by an amount DV is directly proportional to the fractional change DV/V0 in the volume:
V0, where V and V0 are the final and initial volumes, respectively. Such a pressure change occurs, for example, when a swimmer dives deeper into the water. Experiment reveals that the change DP in pressure needed to change the volume by an amount DV is directly proportional to the fractional change DV/V0 in the volume: