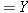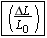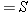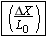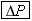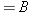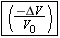10.8. Stress, Strain, and Hooke’s Law

Equations 10.17, 10.18, and 10.20 specify the amount of force needed for a given amount of elastic deformation, and they are repeated in Table 10.4 to emphasize their common features. The left side of each equation is the magnitude of the force per unit area required to cause an elastic deformation. In general, the ratio of the magnitude of the force to the area is called the stress. The right side of each equation involves the change in a quantity (DL, DX, or DV) divided by a quantity (L₀ or V₀) relative to which the change is compared. The terms DL/L₀, DX/L₀, and DV/V₀ are unitless ratios, and each is referred to as the strain that results from the applied stress. In the case of stretch and compression, the strain is the fractional change in length, whereas in volume deformation it is the fractional change in volume. In shear deformation the strain refers to a change in shape of the object. Experiments show that these three equations, with constant values for Young’s modulus, the shear modulus, and the bulk modulus, apply to a wide range of materials. Therefore, stress and strain are directly proportional to one another, a relationship first discovered by Robert Hooke (1635–1703) and now referred to as Hooke’s law.

Table 10.4 Stress and Strain Relations for Elastic Behaviour

(10.17)

(10.18)

(10.20)

HOOKE’S LAW FOR STRESS AND STRAIN

Stress is directly proportional to strain.

SI Unit of Stress: newton per square meter = pascal (Pa)

SI Unit of Strain: Strain is a unitless quantity.

In reality, materials obey Hooke’s law only up to a certain limit, as Figure 10.34 shows. As long as stress remains proportional to strain, a plot of stress versus strain is a straight line. The point on the graph where the material begins to deviate from straight-line behavior is called the “proportionality limit.” Beyond the proportionality limit stress and strain are no longer directly proportional. However, if the stress does not exceed the “elastic limit” of the material, the object will return to its original size and shape once the stress is removed. The “elastic limit” is the point beyond which the object no longer returns to its original size and shape when the stress is removed; the object remains permanently deformed.

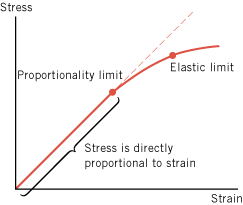Hookes law (stress is directly proportional to strain) is valid only up to the proportionality limit of a material. Beyond this limit, Hookes law no longer applies. Beyond the elastic limit, the material remains deformed even when the stress is removed.

Figure 10.34 Hooke’s law (stress is directly proportional to strain) is valid only up to the proportionality limit of a material. Beyond this limit, Hooke’s law no longer applies. Beyond the elastic limit, the material remains deformed even when the stress is removed.

Self-Assessment Test 10.2

Test your understanding of the material in Sections 10.3, 10.4, 10.5, 10.6, 10.7 and 10.8:

· Energy and Simple Harmonic Motion ·The Pendulum ·Damped Harmonic Motion and Resonance ·Elastic Deformation