13.2.
Conduction
Anyone who has fried a hamburger in an all-metal skillet knows that the metal handle becomes hot. Somehow, heat is transferred from the burner to the handle. Clearly, heat is not being transferred by the bulk movement of the metal or the surrounding air, so convection can be ruled out. Instead, heat is transferred directly through the metal by a process called conduction.
| CONDUCTION |
|
Conduction is the process whereby heat is transferred directly through a material, with any bulk motion of the material playing no role in the transfer.
|
One mechanism for conduction occurs when the atoms or molecules in a hotter part of the material vibrate or move with greater energy than those in a cooler part. By means of collisions, the more energetic molecules pass on some of their energy to their less energetic neighbors. For example, imagine a gas filling the space between two walls that face each other and are maintained at different temperatures. Molecules strike the hotter wall, absorb energy from it, and rebound with a greater kinetic energy than when they arrived. As these more energetic molecules collide with their less energetic neighbors, they transfer some of their energy to them. Eventually, this energy is passed on until it reaches the molecules next to the cooler wall. These molecules, in turn, collide with the wall, giving up some of their energy to it in the process. Through such molecular collisions, heat is conducted from the hotter to the cooler wall.
A similar mechanism for the conduction of heat occurs in metals. Metals are different from most substances in having a pool of electrons that are more or less free to wander throughout the metal. These free electrons can transport energy and allow metals to transfer heat very well. The free electrons are also responsible for the excellent electrical conductivity that metals have.
Those materials that conduct heat well are called thermal conductors, and those that conduct heat poorly are known as thermal insulators. Most metals are excellent thermal conductors; wood, glass, and most plastics are common thermal insulators. Thermal insulators have many important applications. Virtually all new housing construction incorporates thermal insulation in attics and walls to reduce heating and cooling costs. And the wooden or plastic handles on many pots and pans reduce the flow of heat to the cook’s hand.
To illustrate the factors that influence the conduction of heat, Figure 13.8 displays a rectangular bar. The ends of the bar are in thermal contact with two bodies, one of which is kept at a constant higher temperature, while the other is kept at a constant lower temperature. Although not shown for the sake of clarity, the sides of the bar are insulated, so the heat lost through them is negligible. The amount of heat Q conducted through the bar from the warmer end to the cooler end depends on a number of factors:
| | 1. |
Q is proportional to the time t during which conduction takes place (Q 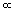  t). More heat flows in longer time periods. t). More heat flows in longer time periods.
|
| | 2. |
Q is proportional to the temperature difference DT between the ends of the bar (Q 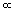  DT). A larger difference causes more heat to flow. No heat flows when both ends have the same temperature, so that DT DT). A larger difference causes more heat to flow. No heat flows when both ends have the same temperature, so that DT = = 0 C°. 0 C°.
|
| | 3. |
Q is proportional to the cross-sectional area A of the bar (Q 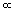  A). Figure 13.9 helps to explain this fact by showing two identical bars (insulated sides not shown) placed between the warmer and cooler bodies. Clearly, twice as much heat flows through two bars as through one, since the cross-sectional area has been doubled. A). Figure 13.9 helps to explain this fact by showing two identical bars (insulated sides not shown) placed between the warmer and cooler bodies. Clearly, twice as much heat flows through two bars as through one, since the cross-sectional area has been doubled.
|
| | 4. |
Q is inversely proportional to the length L of the bar (Q 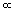  1/L). Greater lengths of material conduct less heat. To experience this effect, put two insulated mittens (the pot holders that cooks keep around the stove) on the same hand. Then, touch a hot pot and notice that it feels cooler than when you wear only one mitten, signifying that less heat passes through the greater thickness (“length”) of material. 1/L). Greater lengths of material conduct less heat. To experience this effect, put two insulated mittens (the pot holders that cooks keep around the stove) on the same hand. Then, touch a hot pot and notice that it feels cooler than when you wear only one mitten, signifying that less heat passes through the greater thickness (“length”) of material.
|
These proportionalities can be stated together as Q
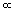
 (A DT)t/L. Equation 13.1 expresses this result with the aid of a proportionality constant k, which is called the thermal conductivity.
(A DT)t/L. Equation 13.1 expresses this result with the aid of a proportionality constant k, which is called the thermal conductivity.
 | | Figure 13.8
Heat is conducted through the bar when the ends of the bar are maintained at different temperatures. The heat flows from the warmer to the cooler end. |
|
| CONDUCTION OF HEAT THROUGH A MATERIAL |
|
The heat Q conducted during a time t through a bar of length L and cross-sectional area A is
 | (13.1) |  |
where DT is the temperature difference between the ends of the bar and k is the thermal conductivity of the material.
SI Unit of Thermal Conductivity: J/(s·m·C°)
|
 | | Figure 13.9
Twice as much heat flows through two identical bars as through one. |
|
 Concept Simulation 13.1 Concept Simulation 13.1 |
 |
When heat is transferred through a bar, as illustrated in Figure 13.8, the amount of heat conducted per second depends on the length and cross-sectional area of the bar, as well as the temperature of each end. In this simulation the user can vary each of these parameters and see their effect on the energy flow. Related Homework: Problems 1, 28 |
|
 |
Since k =
= QL/(tA DT), the SI unit for thermal conductivity is J·m/(s·m2·C°) or J/(s·m·C°). The SI unit of power is the joule per second (J/s) or watt (W), so the thermal conductivity is also given in units of W/(m·C°).
QL/(tA DT), the SI unit for thermal conductivity is J·m/(s·m2·C°) or J/(s·m·C°). The SI unit of power is the joule per second (J/s) or watt (W), so the thermal conductivity is also given in units of W/(m·C°).
Different materials have different thermal conductivities, and Table 13.1 gives some representative values. Because metals are such good thermal conductors, they have large thermal conductivities. In comparison, liquids and gases generally have small thermal conductivities. In fact, in most fluids the heat transferred by conduction is negligible compared to that transferred by convection when there are strong convection currents. Air, for instance, with its small thermal conductivity, is an excellent thermal insulator when confined to small spaces where no appreciable convection currents can be established. Goose down, Styrofoam, and wool derive their fine insulating properties in part from the small dead-air spaces within them, as Figure 13.10 illustrates. We also take advantage of dead-air spaces when we dress “in layers” during very cold weather and put on several layers of relatively thin clothing rather than one thick layer. The air trapped between the layers acts as an excellent insulator.
 | | Figure 13.10
Styrofoam is an excellent thermal insulator because it contains many small, dead-air spaces. These small spaces inhibit heat transfer by convection currents, and air itself has a very low thermal conductivity. |
|
| Table 13.1
Thermal Conductivitiesa of Selected Materials |
|
Substance
|
Thermal Conductivity, k [J/(s·m·C°)]
| |
Metals
|
Aluminum
|
240
|
Brass
|
110
|
Copper
|
390
|
Iron
|
79
|
Lead
|
35
|
Silver
|
420
|
Steel (stainless)
|
14
|
Gases
|
Air
|
0.0256
|
Hydrogen (H2)
|
0.180
|
Nitrogen (N2)
|
0.0258
|
Oxygen (O2)
|
0.0265
|
Other Materials
|
Asbestos
|
0.090
|
Body fat
|
0.20
|
Concrete
|
1.1
|
Diamond
|
2450
|
Glass
|
0.80
|
Goose down
|
0.025
|
Ice (0 °C)
|
2.2
|
Styrofoam
|
0.010
|
Water
|
0.60
|
Wood (oak)
|
0.15
|
Wool
|
0.040
|
| |
|
Example 2 deals with the role that conduction through body fat plays in regulating body temperature.
| Example 2 Heat Transfer in the Human Body |
 |
|
When excessive heat is produced within the body, it must be transferred to the skin and dispersed if the temperature at the body interior is to be maintained at the normal value of 37.0 °C. One possible mechanism for transfer is conduction through body fat. Suppose that heat travels through 0.030 m of fat in reaching the skin, which has a total surface area of 1.7 m2 and a temperature of 34.0 °C. Find the amount of heat that reaches the skin in half an hour (1800 s).
Reasoning and Solution
In Table 13.1 the thermal conductivity of body fat is given as k = = 0.20 J/(s·m·C°). According to Equation 13.1, 0.20 J/(s·m·C°). According to Equation 13.1,
For comparison, a jogger can generate over ten times this amount of heat in a half hour. Thus, conduction through body fat is not a particularly effective way of removing excess heat. Heat transfer via blood flow to the skin is more effective and has the added advantage that the body can vary the blood flow as needed (see Problem 7).
|
 |
Virtually all homes contain insulation in the walls to reduce heat loss. Example 3 illustrates how to determine this loss with and without insulation.
| Example 3 Layered Insulation |
 |
|
One wall of a house consists of 0.019-m-thick plywood backed by 0.076-m-thick insulation, as Figure 13.11 shows. The temperature at the inside surface is 25.0 °C, while the temperature at the outside surface is 4.0 °C, both being constant. The thermal conductivities of the insulation and the plywood are, respectively, 0.030 and 0.080 J/(s·m·C°), and the area of the wall is 35 m2. Find the heat conducted through the wall in one hour (a) with the insulation and (b) without the insulation.
 | | Figure 13.11
Heat flows through the insulation and plywood from the warmer inside to the cooler outside. The temperature of the insulation-plywood interface is T. |
|
Reasoning
The temperature T at the insulation-plywood interface (see Figure 13.11) must be determined before the heat conducted through the wall can be obtained. In calculating this temperature, we use the fact that no heat is accumulating in the wall because the inner and outer temperatures are constant. Therefore, the heat conducted through the insulation must equal the heat conducted through the plywood during the same time; that is, Qinsulation = = Qplywood. Each of the Q values can be expressed as Q Qplywood. Each of the Q values can be expressed as Q = = (kA DT)t/L, according to Equation 13.1, leading to an expression that can be solved for the interface temperature. Once a value for T is available, Equation 13.1 can be used to obtain the heat conducted through the wall. (kA DT)t/L, according to Equation 13.1, leading to an expression that can be solved for the interface temperature. Once a value for T is available, Equation 13.1 can be used to obtain the heat conducted through the wall.
Problem solving insight
When heat is conducted through a multi-layered material, and the high and low temperatures are constant, the heat conducted through each layer is the same. |
|
Solution
| (a) |
Using Equation 13.1 and the fact that Qinsulation = = Qplywood, we find that
Eliminating the area A and time t algebraically and solving this equation for T reveals that the temperature at the insulation-plywood interface is T Qplywood, we find that
Eliminating the area A and time t algebraically and solving this equation for T reveals that the temperature at the insulation-plywood interface is T = = 5.8 °C.
The heat conducted through the wall is either Qinsulation or Qplywood, since the two quantities are equal. Choosing Qinsulation and using T 5.8 °C.
The heat conducted through the wall is either Qinsulation or Qplywood, since the two quantities are equal. Choosing Qinsulation and using T = = 5.8 °C in Equation 13.1, we find that 5.8 °C in Equation 13.1, we find that
| | (b) |
It is straightforward to use Equation 13.1 to calculate the amount of heat that would flow through the plywood in one hour if the insulation were absent:
Without insulation, the heat loss is increased by a factor of about 12.
|
|
 |
Fruit growers sometimes protect their crops by spraying them with water when overnight temperatures are expected to drop below freezing. Some fruit crops, like the blueberry plants in Figure 13.12, can withstand temperatures down to freezing (0 °C). However, as the temperature falls below freezing, the risk of damage rises significantly. When water is sprayed on the plants, it can freeze and form a covering of ice. When the water freezes it releases heat (see Section 12.8), some of which goes into warming the plant. In addition, both water and ice have relatively small thermal conductivities, as Table 13.1 indicates. Thus, they also protect the crop by acting as thermal insulators that reduce heat loss from the plants.
 | | Figure 13.12
After a subfreezing night, this blueberry crop is being checked for freeze damage. The plants were sprayed the previous evening by sprinklers that put a coating of ice on them, thereby insulating the plants against the subfreezing temperatures. (© AP/Wide World Photos) |
|
Although a layer of ice may be beneficial to blueberry plants, it is not so desirable inside a refrigerator, as Conceptual Example 4 discusses.
| Conceptual Example 4 An Iced-up Refrigerator |
 |
|
In a refrigerator, heat is removed by a cold refrigerant fluid that circulates within a tubular space embedded within a metal plate, as Figure 13.13 illustrates. A good refrigerator cools food as quickly as possible. Decide whether the plate should be made from aluminum or stainless steel and whether the arrangement works better or worse when it becomes coated with a layer of ice.
 | | Figure 13.13
In a refrigerator, cooling is accomplished by a cold refrigerant fluid that circulates through a tubular space embedded within an aluminum plate. The arrangement works less well when the plate is coated with a layer of ice. |
|
Reasoning and Solution Figure 13.13 (see blowups) shows the metal cooling plate with and without a layer of ice. Without ice, heat passes by conduction through the metal to the refrigerant fluid within. For a given temperature difference across the thickness of metal, heat is transferred more quickly through the metal with the largest thermal conductivity. Table 13.1 indicates that the thermal conductivity of aluminum is more than 17 times larger than that of stainless steel. Therefore, the plate should be made from aluminum. When the plate becomes coated with ice, any heat that is removed by the refrigerant fluid must first be transferred by conduction through the ice before it encounters the aluminum plate. But the conduction of heat through ice occurs much less readily than through aluminum, because, as Table 13.1 indicates, ice has a much smaller thermal conductivity. Moreover, Equation 13.1 indicates that the heat conducted per unit time (Q/t) is inversely proportional to the thickness L of the ice. Thus, as ice builds up, the heat removed per unit time by the cooling plate decreases. When covered with ice, the cooling plate works less well.
Related Homework:
Problem 34
|
 |
 |
 Interactive LearningWare 13.1 Interactive LearningWare 13.1 | A hollow, cylindrical glass tube is filled with hydrogen (H2) gas. The tube has a length of 0.25 m and inner and outer radii of 0.020 and 0.023 m, respectively. One end of the tube is maintained at a temperature of 85 °C, while the other is kept at 15 °C. There is no heat loss through the curved surface. The thermal conductivity of glass is 0.80 J/(s·m·C°); the thermal conductivity of hydrogen is 0.18 J/(s·m·C°). Determine the total heat that flows through the tube (both the glass and the hydrogen) in a time of 55 s. Related Homework: Problem 8 |
|
 |
| Check Your Understanding 1 |
 |
| Copyright © 2000-2003 by John Wiley & Sons, Inc. or related companies. All rights reserved. |
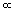
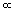
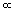
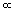
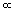
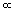
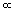
![]()
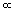
![]() (A DT)t/L. Equation 13.1 expresses this result with the aid of a proportionality constant k, which is called the thermal conductivity.
(A DT)t/L. Equation 13.1 expresses this result with the aid of a proportionality constant k, which is called the thermal conductivity.

 Concept Simulation 13.1
Concept Simulation 13.1![]() =
=![]() QL/(tA DT), the SI unit for thermal conductivity is J·m/(s·m2·C°) or J/(s·m·C°). The SI unit of power is the joule per second (J/s) or watt (W), so the thermal conductivity is also given in units of W/(m·C°).
QL/(tA DT), the SI unit for thermal conductivity is J·m/(s·m2·C°) or J/(s·m·C°). The SI unit of power is the joule per second (J/s) or watt (W), so the thermal conductivity is also given in units of W/(m·C°).
