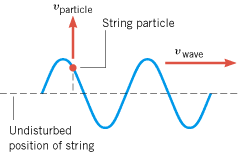
Is the speed of a transverse wave on a string the same as the speed at which a particle on the string moves (see Figure 16.10)?

Figure 16.10  A transverse wave on a string is moving to the right with a constant speed vwave. A string particle moves up and down in simple harmonic motion about the undisturbed position of the string. The speed of the particle vparticle changes from moment to moment as the wave passes.

Reasoning and Solution The particle speed v_particle specifies how fast the particle is moving as it oscillates up and down, and it is different from the wave speed. If the source of the wave (e.g., the hand in Figure 16.2c) vibrates in simple harmonic motion, each string particle vibrates in a like manner, with the same amplitude and frequency as the source. Moreover, the particle speed, unlike the wave speed, is not constant. As for any object in simple harmonic motion, the particle speed is greatest when the particle is passing through the undisturbed position of the string and zero when the particle is at its maximum displacement. According to Equation 10.7, the particle speed depends on the amplitude A, the angular frequency w, and the time t through the relation v_particle=Aw sin wt, where the minus sign has been omitted because we are interested only in the speed, which is the magnitude of the particle’s velocity. Thus, the speed of a string particle is determined by the properties of the source creating the wave and not by the properties of the string itself. In contrast, the speed of the wave is determined by the properties of the string—that is, the tension F and the mass per unit length m/L, according to Equation 16.2. We see, then, that the two speeds, v_wave and v_particle, are not the same.

Related Homework: Conceptual Question 4, Problems 18, 99