|
During a fireworks display, a rocket explodes high in the air, as Figure 16.24 illustrates. Assume that the sound spreads out uniformly in all directions and that reflections from the ground can be ignored. When the sound reaches listener 2, who is r2 = = 640 m away from the explosion, the sound has an intensity of I2 640 m away from the explosion, the sound has an intensity of I2 = = 0.10 W/m2. What is the sound intensity detected by listener 1, who is r1 0.10 W/m2. What is the sound intensity detected by listener 1, who is r1 = = 160 m away from the explosion? 160 m away from the explosion?
 | Figure 16.24
If an explosion in a fireworks display radiates sound uniformly in all directions, the intensity at any distance r is I
 =
=
 P/(4p
r
2), where P is the sound power of the explosion.
P/(4p
r
2), where P is the sound power of the explosion. |
|
Reasoning
Listener 1 is four times closer to the explosion than listener 2. Therefore, the sound intensity detected by listener 1 is 42 = = 16 times greater than that detected by listener 2. 16 times greater than that detected by listener 2.
Problem solving insight
Equation 16.9 can be used only when the sound spreads out uniformly in all directions and there are no reflections of the sound waves. |
|
Solution
The ratio of the sound intensities can be found using Equation 16.9:
As a result, I1 = = (16)I2 (16)I2 = = (16)(0.10 W/m2) (16)(0.10 W/m2) = = 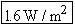 . .
|
![]() =
=![]() 640 m away from the explosion, the sound has an intensity of I2
640 m away from the explosion, the sound has an intensity of I2![]() =
=![]() 0.10 W/m2. What is the sound intensity detected by listener 1, who is r1
0.10 W/m2. What is the sound intensity detected by listener 1, who is r1![]() =
=![]() 160 m away from the explosion?
160 m away from the explosion?
![]() =
=![]() 16 times greater than that detected by listener 2.
16 times greater than that detected by listener 2.
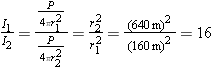
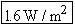 .
.