Figure 16.38 shows waves traveling on two strings. Each string is attached to a wall at one end and to a box that has a weight of 28.0 N at the other end. String 1 has a mass of 8.00 g and a length of 4.00 cm, and string 2 has a mass of 12.0 g and a length of 8.00 cm. Determine the speed of the wave on each string.
 |
|
Is the tension the same in each string?
Yes, the tension is the same. The two strings support the box, so the tension in each string is one-half the weight of the box. The fact that the strings have different masses and lengths does not affect the tension, which is determined only by the weight of the hanging box.Is the speed of each wave the same?
Not necessarily. The speed of a wave on a string depends on both the tension and the linear density, as Equation 16.2 indicates. The tension is the same in both strings, but if the linear densities of the strings are different, the speeds are different.String 1 has a smaller mass and, hence, less inertia than string 2. Does this mean that the speed of the wave on string 1 is greater than that on string 2?
Maybe yes, maybe no. The speed of a wave depends on the linear density of the string, which is its mass divided by its length. Depending on the lengths of the strings, string 1 could have a larger linear density and, hence, smaller speed, than string 2. The solution below illustrates this point.Solution
The speed of a wave on a string is given by Equation 16.2 as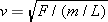 
, where F is the tension and m/L is the mass per unit length, or linear density. Since both strings support the box, the tension in each is one-half the weight of the box, or
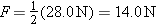. The linear densities of the strings are
 |  |
 | |
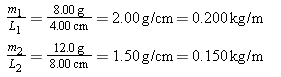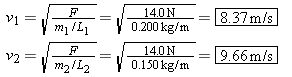