16.2.
Periodic Waves
 CONCEPTS AT A GLANCE The transverse and longitudinal waves that we have been discussing are called periodic waves because they consist of cycles or patterns that are produced over and over again by the source. In Figures 16.2 and 16.3 the repetitive patterns occur as a result of the simple harmonic motion of the left end of the Slinky. Every segment of the Slinky vibrates in simple harmonic motion. Sections 10.1 and 10.2 discuss the simple harmonic motion of an object on a spring and introduce the concepts of cycle, amplitude, period, and frequency. As the Concepts-at-a-Glance chart in Figure 16.5 illustrates, this same terminology is used to describe periodic waves, such as the sound waves we hear and the light waves we see (discussed in Chapter 24).
CONCEPTS AT A GLANCE The transverse and longitudinal waves that we have been discussing are called periodic waves because they consist of cycles or patterns that are produced over and over again by the source. In Figures 16.2 and 16.3 the repetitive patterns occur as a result of the simple harmonic motion of the left end of the Slinky. Every segment of the Slinky vibrates in simple harmonic motion. Sections 10.1 and 10.2 discuss the simple harmonic motion of an object on a spring and introduce the concepts of cycle, amplitude, period, and frequency. As the Concepts-at-a-Glance chart in Figure 16.5 illustrates, this same terminology is used to describe periodic waves, such as the sound waves we hear and the light waves we see (discussed in Chapter 24).
|
| Figure 16.5
CONCEPTS AT A GLANCE For periodic waves, the terms cycle, amplitude, period, and frequency have the same meaning as they do in simple harmonic motion. Sound, such as that produced by these musicians, is a periodic wave and is described using this terminology. (© Andy Sacks/Stone/Getty Images) |
|
Figure 16.6 uses a graphical representation of a transverse wave to review this terminology. One cycle of a wave is shaded in color in both parts of the drawing. A wave is a series of many cycles. In part a the vertical position of the Slinky is plotted on the vertical axis, and the corresponding distance along the length of the Slinky is plotted on the horizontal axis. Such a graph is equivalent to a photograph of the wave taken at one instant in time and shows the disturbance that exists at each point along the Slinky’s length. As marked on this graph, the amplitude A is the maximum excursion of a particle of the medium from the particle’s undisturbed position. The amplitude is the distance between a crest, or highest point on the wave pattern, and the undisturbed position; it is also the distance between a trough, or lowest point on the wave pattern, and the undisturbed position. The wavelength l is the horizontal length of one cycle of the wave, as shown in Figure 16.6a. The wavelength is also the horizontal distance between two successive crests, two successive troughs, or any two successive equivalent points on the wave.
|
| Figure 16.6
One cycle of the wave is shaded in color, and the amplitude of the wave is denoted as A. |
|
Part b of Figure 16.6 shows a graph in which time, rather than distance, is plotted on the horizontal axis. This graph is obtained by observing a single point on the Slinky. As the wave passes, the point under observation oscillates up and down in simple harmonic motion. As indicated on the graph, the period T is the time required for one complete up/down cycle, just as it is for an object vibrating on a spring. Equivalently, the period is the time required for the wave to travel a distance of one wavelength. The period T is related to the frequency f, just as it is for any example of simple harmonic motion:
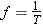 | (10.5) |  |
The period is commonly measured in seconds, and frequency is measured in cycles per second or hertz (Hz). If, for instance, one cycle of a wave takes one-tenth of a second to pass an observer, then ten cycles pass per second, as Equation 10.5 indicates [f =
= 1/(0.1 s)
1/(0.1 s) =
= 10 cycles/s
10 cycles/s =
= 10 Hz].
10 Hz].
A simple relation exists between the period, the wavelength, and the speed of a wave, a relation that Figure 16.7 helps to introduce. Imagine waiting at a railroad crossing, while a freight train moves by at a constant speed v. The train consists of a long line of identical boxcars, each of which has a length l and requires a time T to pass, so the speed is v =
= l/T. This same equation applies for a wave and relates the speed of the wave to the wavelength l and the period T. Since the frequency of a wave is f
l/T. This same equation applies for a wave and relates the speed of the wave to the wavelength l and the period T. Since the frequency of a wave is f =
= 1/T, the expression for the speed is
1/T, the expression for the speed is
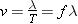 | (16.1) |  |
The terminology just discussed and the fundamental relations f =
= 1/T and v
1/T and v =
= fl apply to longitudinal as well as to transverse waves. Example 1 illustrates how the wavelength of a wave is determined by the wave speed and the frequency established by the source.
fl apply to longitudinal as well as to transverse waves. Example 1 illustrates how the wavelength of a wave is determined by the wave speed and the frequency established by the source.
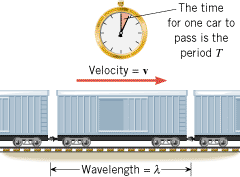 | | Figure 16.7
A train moving at a constant speed serves as an analogy for a traveling wave. |
|
| Example 1 The Wavelengths of Radio Waves |
 |
| Copyright © 2000-2003 by John Wiley & Sons, Inc. or related companies. All rights reserved. |
![]() CONCEPTS AT A GLANCE The transverse and longitudinal waves that we have been discussing are called periodic waves because they consist of cycles or patterns that are produced over and over again by the source. In Figures 16.2 and 16.3 the repetitive patterns occur as a result of the simple harmonic motion of the left end of the Slinky. Every segment of the Slinky vibrates in simple harmonic motion. Sections 10.1 and 10.2 discuss the simple harmonic motion of an object on a spring and introduce the concepts of cycle, amplitude, period, and frequency. As the Concepts-at-a-Glance chart in Figure 16.5 illustrates, this same terminology is used to describe periodic waves, such as the sound waves we hear and the light waves we see (discussed in Chapter 24).
CONCEPTS AT A GLANCE The transverse and longitudinal waves that we have been discussing are called periodic waves because they consist of cycles or patterns that are produced over and over again by the source. In Figures 16.2 and 16.3 the repetitive patterns occur as a result of the simple harmonic motion of the left end of the Slinky. Every segment of the Slinky vibrates in simple harmonic motion. Sections 10.1 and 10.2 discuss the simple harmonic motion of an object on a spring and introduce the concepts of cycle, amplitude, period, and frequency. As the Concepts-at-a-Glance chart in Figure 16.5 illustrates, this same terminology is used to describe periodic waves, such as the sound waves we hear and the light waves we see (discussed in Chapter 24).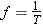
![]() =
=![]() 1/(0.1 s)
1/(0.1 s)![]() =
=![]() 10 cycles/s
10 cycles/s![]() =
=![]() 10 Hz].
10 Hz].![]() =
=![]() l/T. This same equation applies for a wave and relates the speed of the wave to the wavelength l and the period T. Since the frequency of a wave is f
l/T. This same equation applies for a wave and relates the speed of the wave to the wavelength l and the period T. Since the frequency of a wave is f![]() =
=![]() 1/T, the expression for the speed is
1/T, the expression for the speed is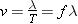
![]() =
=![]() 1/T and v
1/T and v![]() =
=![]() fl apply to longitudinal as well as to transverse waves. Example 1 illustrates how the wavelength of a wave is determined by the wave speed and the frequency established by the source.
fl apply to longitudinal as well as to transverse waves. Example 1 illustrates how the wavelength of a wave is determined by the wave speed and the frequency established by the source.