16.6. The Speed of Sound
GASES
Sound travels through gases, liquids, and solids at considerably different speeds, as Table 16.1 reveals. Near room temperature, the speed of sound in air is 343 m/s (767 mi/h) and is markedly greater in liquids and solids. For example, sound travels more than four times faster in water and more than seventeen times faster in steel than it does in air. In general, sound travels slowest in gases, faster in liquids, and fastest in solids.
| Table 16.1 Speed of Sound in Gases, Liquids, and Solids | |||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||
Like the speed of a wave on a guitar string, the speed of sound depends on the properties of the medium. In a gas, it is only when molecules collide that the condensations and rarefactions of a sound wave can move from place to place. It is reasonable, then, to expect the speed of sound in a gas to have the same order of magnitude as the average molecular speed between collisions. For an ideal gas this average speed is the translational rms speed given by Equation 14.6: 
, where T is the Kelvin temperature, m is the mass of a molecule, and k is Boltzmann’s constant. Although the expression for vrms overestimates the speed of sound, it does give the correct dependence on Kelvin temperature and particle mass. Careful analysis shows that the speed of sound in an ideal gas is given by
 |  |
where g=cP/cV is the ratio of the specific heat capacity at constant pressure cP to the specific heat capacity at constant volume cV.
The factor g is introduced in Section 15.5, where the adiabatic compression and expansion of an ideal gas is discussed. It appears in Equation 16.5 because the condensations and rarefactions of a sound wave are formed by adiabatic compressions and expansions of the gas. The regions that are compressed (the condensations) become slightly warmed, and the regions that are expanded (the rarefactions) become slightly cooled. However, no appreciable heat flows from a condensation to an adjacent rarefaction because the distance between the two (half a wavelength) is relatively large for most audible sound waves and a gas is a poor thermal conductor. Thus, the compression and expansion process is adiabatic. Example 4 illustrates the use of Equation 16.5.
| Example 4 An Ultrasonic Ruler |
| Check Your Understanding 2 |
| |
| |
|
Sonar (sound navigation ranging) is a technique for determining water depth and locating underwater objects, such as reefs, submarines, and schools of fish. The core of a sonar unit consists of an ultrasonic transmitter and receiver mounted on the bottom of a ship. The transmitter emits a short pulse of ultrasonic sound, and at a later time the reflected pulse returns and is detected by the receiver. The water depth is determined from the electronically measured round-trip time of the pulse and a knowledge of the speed of sound in water; the depth registers automatically on an appropriate meter. Such a depth measurement is similar to the distance measurement discussed for the ultrasonic ruler in Example 4.
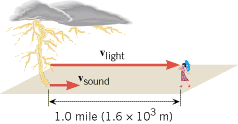
Conceptual Example 5 illustrates how the speed of sound in air can be used to estimate the distance to a thunderstorm, using a handy rule of thumb.
| Conceptual Example 5 Lightning, Thunder, and a Rule of Thumb |
 | |||
|
There is a rule of thumb for estimating how far away a thunderstorm is. After you see a flash of lightning, count off the seconds until the thunder is heard. Divide the number of seconds by five. The result gives the approximate distance (in miles) to the thunderstorm. Why does this rule work? Reasoning and Solution Figure 16.20 shows a lightning bolt and a person who is standing one mile (1.6
| |||
 | |||
LIQUIDS
In a liquid, the speed of sound depends on the density r and the adiabatic bulk modulus Bad of the liquid:
 | |
The bulk modulus is introduced in Section 10.7 in a discussion of the volume deformation of liquids and solids. There it is tacitly assumed that the temperature remains constant while the volume of the material changes; that is, the compression or expansion is isothermal. However, the condensations and rarefactions in a sound wave occur under adiabatic rather than isothermal conditions. Thus, the adiabatic bulk modulus Bad must be used when calculating the speed of sound in liquids. Values of Bad will be provided as needed in this text.
| Need more practice? |
| ||
| ||
|
SOLID BARS
When sound travels through a long slender solid bar, the speed of the sound depends on the properties of the medium according to
 | |
where Y is Young’s modulus (defined in Section 10.7) and r is the density.
|
