16.7.
Sound Intensity
Sound waves carry energy that can be used to do work, like forcing the eardrum to vibrate. In an extreme case such as a sonic boom, the energy can be sufficient to cause damage to windows and buildings. The amount of energy transported per second by a sound wave is called the power of the wave and is measured in SI units of joules per second (J/s) or watts (W).
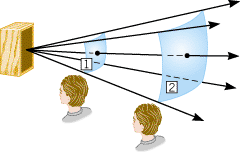 | | Figure 16.21
The power carried by a sound wave spreads out after leaving a source, such as a loudspeaker. Thus, the power passes perpendicularly through surface 1 and then through surface 2, which has the larger area. |
|
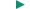 CONCEPTS AT A GLANCE When a sound wave leaves a source, such as the loudspeaker in Figure 16.21, the power spreads out and passes through imaginary surfaces that have increasingly larger areas. For instance, the same sound power passes through the surfaces labeled 1 and 2 in the drawing. However, the power is spread out over a greater area in surface 2. The Concepts-at-a-Glance chart in Figure 16.22 indicates how we take this spreading-out effect into account. We will bring together the ideas of sound power and the area through which the power passes and, in the process, formulate the concept of sound intensity. The idea of wave intensity is not confined to sound waves. It will recur, for example, in Chapter 24 when we discuss another important type of waves, electromagnetic waves.
CONCEPTS AT A GLANCE When a sound wave leaves a source, such as the loudspeaker in Figure 16.21, the power spreads out and passes through imaginary surfaces that have increasingly larger areas. For instance, the same sound power passes through the surfaces labeled 1 and 2 in the drawing. However, the power is spread out over a greater area in surface 2. The Concepts-at-a-Glance chart in Figure 16.22 indicates how we take this spreading-out effect into account. We will bring together the ideas of sound power and the area through which the power passes and, in the process, formulate the concept of sound intensity. The idea of wave intensity is not confined to sound waves. It will recur, for example, in Chapter 24 when we discuss another important type of waves, electromagnetic waves.
|
| Figure 16.22
CONCEPTS AT A GLANCE The concept of sound intensity takes into account both the sound power and the area through which the power passes. These children are reacting to the high-intensity sound of rifle fire during a Memorial Day parade. © AP/Wide World Photos) |
|
The sound intensity I is defined as the sound power P that passes perpendicularly through a surface divided by the area A of that surface:
 | (16.8) |  |
The unit of sound intensity is power per unit area, or W/m2. The next example illustrates how the sound intensity changes as the distance from a loudspeaker changes.
| Example 6 Sound Intensities |
 |
|
In Figure 16.21, 12 × × 10–5 W of sound power passes perpendicularly through the surfaces labeled 1 and 2. These surfaces have areas of A1 10–5 W of sound power passes perpendicularly through the surfaces labeled 1 and 2. These surfaces have areas of A1 = = 4.0 m2 and A2 4.0 m2 and A2 = = 12 m2. Determine the sound intensity at each surface and discuss why listener 2 hears a quieter sound than listener 1. 12 m2. Determine the sound intensity at each surface and discuss why listener 2 hears a quieter sound than listener 1.
Reasoning
The sound intensity I is the sound power P passing perpendicularly through a surface divided by the area A of that surface. Since the same sound power passes through both surfaces and surface 2 has the greater area, the sound intensity is less at surface 2.
Problem solving insight
Sound intensity I and sound power P are different concepts. They are related, however, since intensity equals power per unit area. |
|
Solution
The sound intensity at each surface follows from Equation 16.8:
The sound intensity is less at the more distant surface, where the same power passes through a threefold greater area. The ear of a listener, with its fixed area, intercepts less power where the intensity, or power per unit area, is smaller. Thus, listener 2 intercepts less of the sound power than listener 1. With less power striking the ear, the sound is quieter.
|
 |
For a 1000-Hz tone, the smallest sound intensity that the human ear can detect is about 1 ×
× 10–12 W/m2; this intensity is called the threshold of hearing. On the other extreme, continuous exposure to intensities greater than 1 W/m2 can be painful and result in permanent hearing damage. The human ear is remarkable for the wide range of intensities to which it is sensitive.
10–12 W/m2; this intensity is called the threshold of hearing. On the other extreme, continuous exposure to intensities greater than 1 W/m2 can be painful and result in permanent hearing damage. The human ear is remarkable for the wide range of intensities to which it is sensitive.
If a source emits sound uniformly in all directions, the intensity depends on distance in a simple way. Figure 16.23 shows such a source at the center of an imaginary sphere (for clarity only a hemisphere is shown). The radius of the sphere is r. Since all the radiated sound power P passes through the spherical surface of area A =
= 4pr2, the intensity at a distance r is
4pr2, the intensity at a distance r is
 | (16.9) |  |
From this we see that the intensity of a source that radiates sound uniformly in all directions varies as 1/r2. For example, if the distance increases by a factor of two, the sound intensity decreases by a factor of 22 =
= 4. Example 7 illustrates the effect of the 1/r2 dependence of intensity on distance.
4. Example 7 illustrates the effect of the 1/r2 dependence of intensity on distance.
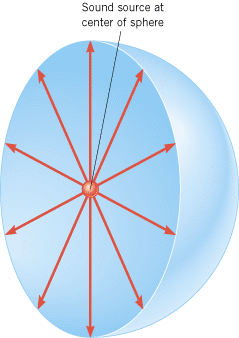 | | Figure 16.23
The sound source at the center of the sphere emits sound uniformly in all directions. In this drawing, only a hemisphere is shown for clarity. |
|
Equation 16.9 is valid only when no walls, ceilings, floors, etc. are present to reflect the sound and cause it to pass through the same surface more than once. Conceptual Example 8 demonstrates why this is so.
| Conceptual Example 8 Reflected Sound and Sound Intensity |
 |
|
Suppose the person singing in the shower in Figure 16.25 produces a sound power P. Sound reflects from the surrounding shower stall. At a distance r in front of the person, does Equation 16.9, I = = P/(4pr2), underestimate, overestimate, or give the correct sound intensity? P/(4pr2), underestimate, overestimate, or give the correct sound intensity?
 | | Figure 16.25
When someone sings in the shower, the sound power passing through part of an imaginary spherical surface (shown in blue) is the sum of the direct sound power and the reflected sound power. |
|
Reasoning and Solution In arriving at Equation 16.9, it was assumed that the sound spreads out uniformly from the source and passes only once through the imaginary surface that surrounds it (see Figure 16.23). Only part of this imaginary surface is shown in Figure 16.25. The drawing illustrates three paths by which the sound passes through the surface. The “direct” sound travels directly along a path from its source to the surface. It is the intensity of the direct sound that is given by I = = P/(4pr2). The remaining paths are two of the many that characterize the sound reflected from the shower stall. The total sound power that passes through the surface is the sum of the direct and reflected powers. Thus, the total sound intensity at a distance r from the source is greater than that of the direct sound alone, and the relation I P/(4pr2). The remaining paths are two of the many that characterize the sound reflected from the shower stall. The total sound power that passes through the surface is the sum of the direct and reflected powers. Thus, the total sound intensity at a distance r from the source is greater than that of the direct sound alone, and the relation I = = P/(4pr2) underestimates the sound intensity from the singing because it does not take into account the reflected sound. People like to sing in the shower because their voices sound so much louder due to the enhanced intensity caused by the reflected sound. P/(4pr2) underestimates the sound intensity from the singing because it does not take into account the reflected sound. People like to sing in the shower because their voices sound so much louder due to the enhanced intensity caused by the reflected sound.
Related Homework:
Problems 52, 64
|
 |
 |
| Copyright © 2000-2003 by John Wiley & Sons, Inc. or related companies. All rights reserved. |


![]() CONCEPTS AT A GLANCE When a sound wave leaves a source, such as the loudspeaker in Figure 16.21, the power spreads out and passes through imaginary surfaces that have increasingly larger areas. For instance, the same sound power passes through the surfaces labeled 1 and 2 in the drawing. However, the power is spread out over a greater area in surface 2. The Concepts-at-a-Glance chart in Figure 16.22 indicates how we take this spreading-out effect into account. We will bring together the ideas of sound power and the area through which the power passes and, in the process, formulate the concept of sound intensity. The idea of wave intensity is not confined to sound waves. It will recur, for example, in Chapter 24 when we discuss another important type of waves, electromagnetic waves.
CONCEPTS AT A GLANCE When a sound wave leaves a source, such as the loudspeaker in Figure 16.21, the power spreads out and passes through imaginary surfaces that have increasingly larger areas. For instance, the same sound power passes through the surfaces labeled 1 and 2 in the drawing. However, the power is spread out over a greater area in surface 2. The Concepts-at-a-Glance chart in Figure 16.22 indicates how we take this spreading-out effect into account. We will bring together the ideas of sound power and the area through which the power passes and, in the process, formulate the concept of sound intensity. The idea of wave intensity is not confined to sound waves. It will recur, for example, in Chapter 24 when we discuss another important type of waves, electromagnetic waves.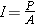
![]() ×
×![]() 10–12 W/m2; this intensity is called the threshold of hearing. On the other extreme, continuous exposure to intensities greater than 1 W/m2 can be painful and result in permanent hearing damage. The human ear is remarkable for the wide range of intensities to which it is sensitive.
10–12 W/m2; this intensity is called the threshold of hearing. On the other extreme, continuous exposure to intensities greater than 1 W/m2 can be painful and result in permanent hearing damage. The human ear is remarkable for the wide range of intensities to which it is sensitive.![]() =
=![]() 4pr2, the intensity at a distance r is
4pr2, the intensity at a distance r is
![]() =
=![]() 4. Example 7 illustrates the effect of the 1/r2 dependence of intensity on distance.
4. Example 7 illustrates the effect of the 1/r2 dependence of intensity on distance.
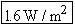 .
.