16.8.
Decibels
The decibel (dB) is a measurement unit used when comparing two sound intensities. The simplest method of comparison would be to compute the ratio of the intensities. For instance, we could compare I =
= 8
8 ×
× 10–12 W/m2 to I0
10–12 W/m2 to I0 =
= 10
10 ×
× –12 W/m2 by computing I/I0
–12 W/m2 by computing I/I0 =
= 8 and stating that I is eight times greater than I0. However, because of the way in which the human hearing mechanism responds to intensity, it is more appropriate to use a logarithmic scale for the comparison. For this purpose, the intensity level b (expressed in decibels) is defined as follows:
8 and stating that I is eight times greater than I0. However, because of the way in which the human hearing mechanism responds to intensity, it is more appropriate to use a logarithmic scale for the comparison. For this purpose, the intensity level b (expressed in decibels) is defined as follows:
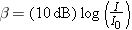 | (16.10) |  |
where “log” denotes the logarithm to the base ten. I0 is the intensity of the reference level to which I is being compared and is often the threshold of hearing, I0 =
= 1.00
1.00 ×
× 10–12 W/m2. With the aid of a calculator, the intensity level can be evaluated for the values of I and I0 given above:
10–12 W/m2. With the aid of a calculator, the intensity level can be evaluated for the values of I and I0 given above:
This result indicates that I is 9 decibels greater than I0. Although b is called the “intensity level,” it is not an intensity and does not have intensity units of W/m2. In fact, the decibel, like the radian, is dimensionless.
Notice that if both I and I0 are at the threshold of hearing, then I =
= I0, and the intensity level is 0 dB according to Equation 16.10:
I0, and the intensity level is 0 dB according to Equation 16.10:
since log 1 =
= 0. Thus, an intensity level of zero decibels does not mean that the sound intensity I is zero; it means that I
0. Thus, an intensity level of zero decibels does not mean that the sound intensity I is zero; it means that I =
= I0.
I0.
Intensity levels can be measured with a sound level meter, such as the one in Figure 16.26. The intensity level b is displayed on its scale, assuming that the threshold of hearing is 0 dB. Table 16.2 lists the intensities I and the associated intensity levels b for some common sounds, using the threshold of hearing as the reference level.
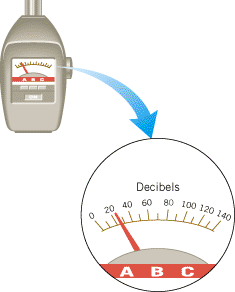 | | Figure 16.26
A sound level meter and a close-up view of its decibel scale. |
|
| Table 16.2
Typical Sound Intensities and Intensity Levels Relative to the Threshold of Hearing |
|
|
Intensity I (W/m2)
|
Intensity Level b (dB)
| |
Threshold of hearing
|
1.0 × × 10 10 – – 12 12
|
0
|
Rustling leaves
|
1.0 × × 10 10 – – 11 11
|
10
|
Whisper
|
1.0 × × 10 10 – – 10 10
|
20
|
Normal conversation (1 meter)
|
1.0 × × 10 10 – – 6 6
|
65
|
Inside car in city traffic
|
1.0 × × 10 10 – – 4 4
|
80
|
Car without muffler
|
1.0 × × 10 10 – – 2 2
|
100
|
Live rock concert
|
1.0
|
120
|
Threshold of pain
|
10
|
130
|
|
|
When a sound wave reaches a listener’s ear, the sound is interpreted by the brain as loud or soft, depending on the intensity of the wave. Greater intensities give rise to louder sounds. However, the relation between intensity and loudness is not a simple proportionality, because doubling the intensity does not double the loudness, as we will now see.
Suppose you are sitting in front of a stereo system that is producing an intensity level of 90 dB. If the volume control on the amplifier is turned up slightly to produce a 91-dB level, you would just barely notice the change in loudness. Hearing tests have revealed that a one-decibel (1-dB) change in the intensity level corresponds to approximately the smallest change in loudness that an average listener with normal hearing can detect. Since 1 dB is the smallest perceivable increment in loudness, a change of 3 dB—say, from 90 to 93 dB—is still a rather small change in loudness. Example 9 determines the factor by which the sound intensity must be increased to achieve such a change.
| Example 9 Comparing Sound Intensities |
To double the loudness of a sound, the intensity must be increased by more than a factor of two. Experiment shows that if the intensity level increases by 10 dB, the new sound seems approximately twice as loud as the original sound. For instance, a 70-dB intensity level sounds about twice as loud as a 60-dB level, and an 80-dB intensity level sounds about twice as loud as a 70-dB level. The factor by which the sound intensity must be increased to double the loudness can be determined by the method used in Example 9:
Solving this equation reveals that I2/I1 =
= 10.0. Thus, increasing the sound intensity by a factor of ten will double the perceived loudness. Consequently, with both audio systems in Figure 16.27 set at maximum volume, the 200-watt system will sound only twice as loud as the much cheaper 20-watt system.
10.0. Thus, increasing the sound intensity by a factor of ten will double the perceived loudness. Consequently, with both audio systems in Figure 16.27 set at maximum volume, the 200-watt system will sound only twice as loud as the much cheaper 20-watt system.
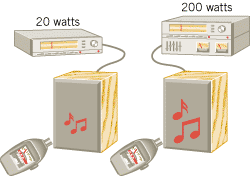 | | Figure 16.27
In spite of its tenfold greater power, the 200-watt audio system has only about double the loudness of the 20-watt system, when both are set for maximum volume. |
|
| Check Your Understanding 3 |
 |
|
The drawing shows a source of sound and two observation points located at distances R1 and R2. The sound spreads uniformly from the source, and there are no reflecting surfaces in the environment. The sound heard at the distance R2 is 6 dB quieter than that heard at the distance R1. (a) What is the ratio I2/R1 of the sound intensities at the two distances? (b) What is the ratio R2/R1 of the distances?
Background:
The intensity level (expressed in decibels) plays the central role in part (a) of this question. In part (b) the facts that the source sends out the sound uniformly and that there are no reflecting surfaces are important. They tell you how the sound intensity depends on distance from the source.
For similar questions (including conceptual counterparts), consult Self-Assessment Test 16.2. This test is described at the end of Section 16.9.
|
|
 |
 |
| Copyright © 2000-2003 by John Wiley & Sons, Inc. or related companies. All rights reserved. |
![]() =
=![]() 8
8![]() ×
×![]() 10–12 W/m2 to I0
10–12 W/m2 to I0![]() =
=![]() 10
10![]() ×
×![]() –12 W/m2 by computing I/I0
–12 W/m2 by computing I/I0![]() =
=![]() 8 and stating that I is eight times greater than I0. However, because of the way in which the human hearing mechanism responds to intensity, it is more appropriate to use a logarithmic scale for the comparison. For this purpose, the intensity level b (expressed in decibels) is defined as follows:
8 and stating that I is eight times greater than I0. However, because of the way in which the human hearing mechanism responds to intensity, it is more appropriate to use a logarithmic scale for the comparison. For this purpose, the intensity level b (expressed in decibels) is defined as follows: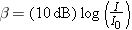
![]() =
=![]() 1.00
1.00![]() ×
×![]() 10–12 W/m2. With the aid of a calculator, the intensity level can be evaluated for the values of I and I0 given above:
10–12 W/m2. With the aid of a calculator, the intensity level can be evaluated for the values of I and I0 given above: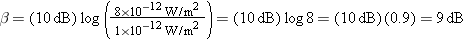
![]() =
=![]() I0, and the intensity level is 0 dB according to Equation 16.10:
I0, and the intensity level is 0 dB according to Equation 16.10: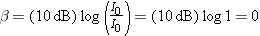
![]() =
=![]() 0. Thus, an intensity level of zero decibels does not mean that the sound intensity I is zero; it means that I
0. Thus, an intensity level of zero decibels does not mean that the sound intensity I is zero; it means that I![]() =
=![]() I0.
I0.
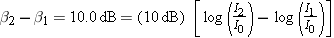
![]() =
=![]() 10.0. Thus, increasing the sound intensity by a factor of ten will double the perceived loudness. Consequently, with both audio systems in Figure 16.27 set at maximum volume, the 200-watt system will sound only twice as loud as the much cheaper 20-watt system.
10.0. Thus, increasing the sound intensity by a factor of ten will double the perceived loudness. Consequently, with both audio systems in Figure 16.27 set at maximum volume, the 200-watt system will sound only twice as loud as the much cheaper 20-watt system.