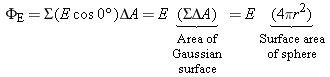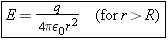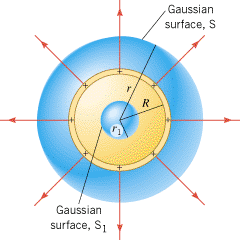
|
Figure 18.35 shows a thin spherical shell of radius R. A positive charge q is spread uniformly over the shell. Find the magnitude of the electric field at any point (a) outside the shell and (b) inside the shell.
 | | Figure 18.35
A uniform distribution of positive charge resides on a thin spherical shell of radius R. The spherical Gaussian surfaces S and S1 are used in Example 14 to evaluate the electric flux outside and inside the shell, respectively. |
|
Reasoning
Because the charge is distributed uniformly over the spherical shell, the electric field is symmetrical. This means that the electric field is directed radially outward in all directions, and its magnitude is the same at all points that are equidistant from the shell. All such points lie on a sphere, so the symmetry is called spherical symmetry. With this symmetry in mind, we will use a spherical Gaussian surface to evaluate the electric flux FE. We will then use Gauss’ law to determine the magnitude of the electric field.
Solution
| (a) |
To find the magnitude of the electric field outside the charged shell, we evaluate the electric flux FE =S(E cos f)DA by using a spherical Gaussian surface of radius r (r > R) that is concentric with the shell. See the surface labeled S in Figure 18.35. Since the electric field E is everywhere perpendicular to the Gaussian surface, f=0° and cos f=1. In addition, E has the same value at all points on the surface, since they are equidistant from the charged shell. Being constant over the surface, E can be factored outside the summation, with the result that
The term SDA is just the sum of the tiny areas that make up the Gaussian surface. Since the area of a spherical surface is 4pr2, we have SDA=4pr2. Setting the electric flux equal to Q/e0, as specified by Gauss’ law, yields E(4pr2)=Q/e0. Since the only charge within the Gaussian surface is the charge q on the shell, it follows that the net charge within the Gaussian surface is Q=q. Thus, we can solve for E and find that
This is a surprising result, for it is the same as that for a point charge (see Equation 18.3 with |q|=q). Thus, the electric field outside a uniformly charged spherical shell is the same as if all the charge q were concentrated as a point charge at the center of the shell.
| | (b) |
To find the magnitude of the electric field inside the charged shell, we select a spherical Gaussian surface that lies inside the shell and is concentric with it. See the surface labeled S1 in Figure 18.35. Inside the charged shell, the electric field (if it exists) must also have spherical symmetry. Therefore, using reasoning like that in part (a), the electric flux through the Gaussian surface is FE=S(E cos f)DA=E(4pr12). In accord with Gauss’ law, the electric flux must be equal to Q/e0, where Q is the net charge inside the Gaussian surface. But now Q=0 C, since all the charge lies on the shell that is outside the surface S1. Consequently, we have E(4pr12)=Q/e0=0, or
Gauss’ law allows us to deduce that there is no electric field inside a uniform spherical shell of charge. An electric field exists only on the outside.
|
|
