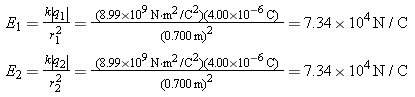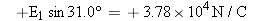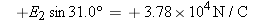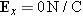Example 17 Becoming Familiar with Electric Fields

Two point charges are lying on the y axis in Figure 18.41a: q₁=–4.00 mC and q₂=+4.00 mC. They are equidistant from the point P, which lies on the x axis. (a) What is the net electric field at P? (b) A small object of charge q₀=+8.00 mC and mass m=1.20 g is placed at P. When it is released, what is its acceleration?

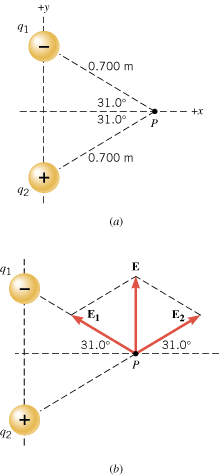(a) Two charges q
1 and q
2 produce an electric field at the point P. (b) The electric fields E

1
and E

2
add to give the net electric field E.

Figure 18.41 (a) Two charges q ₁ and q ₂ produce an electric field at the point P. (b) The electric fields E ₁ and E ₂ add to give the net electric field E.

There is no charge at P in part (a). Is there an electric field at P?

Yes. An electric field is produced by the charges q₁ and q₂, and it exists throughout the entire region that surrounds them. If a test charge were placed at this point, it would experience a force due to the electric field. The force would be the product of the charge and the electric field.

The charge q₁ produces an electric field at the point P. What is the direction of this field?

The electric field created by a charge always points away from a positive charge and toward a negative charge. Since q₁ is negative, the electric field E₁ points toward it (see Figure 18.41b).

What is the direction of the electric field produced by q₂ at P?

Since q₂ is positive, the electric field E₂ that it produces points away from q₂, as shown in the drawing.

Is the magnitude of the net electric field equal to E₁+E₂, where E₁ and E₂ are the magnitudes of the electric fields produced by q₁ and q₂?

No, because the electric fields have different directions. We must add the individual fields as vectors to obtain the net electric field. Only then can we determine its magnitude.

Solution

(a)

The magnitude of the electric fields that q₁ and q₂ produce at P are given by Equation 18.3, where the distances are specified in the drawing:

The x and y components of these fields and the total field E are given in the following table:

Electric field

x component

y component

E₁

E₂

The net electric field E has only a component along the +y axis. So,

(b)

According to Newton’s second law, Equation 4.2, the acceleration a of an object placed at this point is equal to the net force acting on it divided by its mass. The net force F is the product of the charge and the net electric field, F

q₀E, as indicated by Equation 18.2. Thus, the acceleration is