18.5.  Coulomb’s Law

THE FORCE THAT POINT CHARGES EXERT ON EACH OTHER

The electrostatic force that stationary charged objects exert on each other depends on the amount of charge on the objects and the distance between them. Experiments reveal that the greater the charge and the closer together they are, the greater is the force. To set the stage for explaining these features in more detail, Figure 18.10 shows two charged bodies. These objects are so small, compared to the distance r between them, that they can be regarded as mathematical points. The “point charges” have magnitudes |q ₁| and |q ₂|. If the charges have unlike signs, as in part a of the picture, each object is attracted to the other by a force that is directed along the line between them; + F is the electric force exerted on object 1 by object 2 and – F is the electric force exerted on object 2 by object 1. If, as in part b, the charges have the same sign (both positive or both negative), each object is repelled from the other. The repulsive forces, like the attractive forces, act along the line between the charges. Whether attractive or repulsive, the two forces are equal in magnitude but opposite in direction. These forces always exist as a pair, each one acting on a different object, in accord with Newton’s action–reaction law.

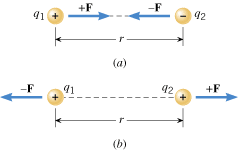Figure 18.10  Each point charge exerts a force on the other. Regardless of whether the forces are (a) attractive or (b) repulsive, they are directed along the line between the charges and have equal magnitudes.

The French physicist Charles-Augustin Coulomb (1736–1806) carried out a number of experiments to determine how the electric force that one point charge applies to another depends on the amount of each charge and the separation between them. His result, now known as Coulomb’s law, is stated below.

COULOMB’S LAW

The magnitude F of the electrostatic force exerted by one point charge q1 on another point charge q2 is directly proportional to the magnitudes |q1| and |q2| of the charges and inversely proportional to the square of the distance r between them:  (18.1)  where k is a proportionality constant whose value in SI units is k=8.99×109 N·m2/C2. The electrostatic force is directed along the line joining the charges, and it is attractive if the charges have unlike signs and repulsive if the charges have like signs.

It is common practice to express k in terms of another constant e₀, by writing k=1/(4pe₀); e₀ is called the permittivity of free space and has a value of e₀=1/(4pk)=8.85×10^–12 C²/(N·m²). Equation 18.1 gives the magnitude of the electrostatic force that each point charge exerts on the other. When using this equation, then, it is important to remember to substitute only the charge magnitudes (without algebraic signs) for |q₁| and |q₂|, as Example 2 illustrates.

Interactive LearningWare 18.1 An object of mass of 215 kg is located just above the surface of the earth (radius=6.38×106 m). Suppose that the object and the earth have an identical charge q. Therefore, two forces — the gravitational force and the electrostatic force — act on the object. Assuming that the earth’s charge is located at the center of the earth, determine q (magnitude and sign) when the object is in equilibrium. Related Homework: Problem 11

Two objects, whose charges are +1.0 and –1.0 C, are separated by 1.0 km. Compared to 1.0 km, the sizes of the objects are small. Find the magnitude of the attractive force that either charge exerts on the other. Reasoning  Considering that the sizes of the objects are small compared to the separation distance, we can treat the charges as point charges. Coulomb’s law may then be used to find the magnitude of the attractive force, provided that only the magnitudes of the charges are used for the symbols |q1| and |q2| that appear in the law. Solution The magnitude of the force is 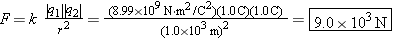 (18.1)

The force calculated in Example 2 corresponds to about 2000 pounds and is so large because charges of ±1.0 C are enormous. Such large charges are encountered only in the most severe conditions, as in a lightning bolt, where as much as 25 coulombs can be transferred between the cloud and the ground. The typical charges produced in the laboratory are much smaller and are measured conveniently in microcoulombs (1 microcoulomb=1 mC=10^–6 C).

Coulomb’s law has a form remarkably similar to Newton’s law of gravitation (F=Gm₁m₂/r²). The force in both laws depends on the inverse square (1/r²) of the distance between the two objects and is directed along the line between them. In addition, the force is proportional to the product of an intrinsic property of each of the objects, the magnitudes of the charges |q₁| and |q₂| in Coulomb’s law and the masses m₁ and m₂ in the gravitation law. But there is a major difference between the two laws. The electrostatic force can be either repulsive or attractive, depending on whether or not the charges have the same sign; in contrast, the gravitational force is always an attractive force.

Section 5.5 discusses how the gravitational attraction between the earth and a satellite provides the centripetal force that keeps a satellite in orbit. Example 3 illustrates that the electrostatic force of attraction plays a similar role in a famous model of the atom created by the Danish physicist Niels Bohr (1885–1962).

In the Bohr model of the hydrogen atom, the electron (–e) is in orbit about the nuclear proton (+e) at a radius of r=5.29×10–11 m, as Figure 18.11 shows. Determine the speed of the electron, assuming the orbit to be circular. 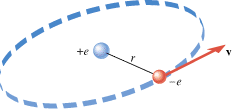Figure 18.11  In the Bohr model of the hydrogen atom, the electron (– e) orbits the proton (+ e) at a distance of r = 5.29 × 10 –11 m. The velocity of the electron is v. Reasoning  Recall from Section 5.2 that any object moving with speed v on a circular path of radius r has a centripetal acceleration of ac=v2/r. This acceleration is directed toward the center of the circle. Newton’s second law specifies that the net force SF needed to create this acceleration is SF=mac=mv2/r, where m is the mass of the object. This equation can be solved for the speed: 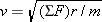. Since the mass of the electron is m=9.11×–31 kg and the radius is given, we can calculate the speed, once a value for the net force is available. For the electron in the hydrogen atom, the net force is provided almost exclusively by the electrostatic force, as given by Coulomb’s law. This force points toward the center of the circle, since the electron and the proton have opposite signs. The electron is also pulled toward the proton by the gravitational force. However, the gravitational force is negligible in comparison to the electrostatic force. Problem solving insight When using Coulomb’s law (F=k |q1||q2|/r2), remember that the symbols |q1| and |q2| stand for the charge magnitudes. Do not substitute negative numbers for these symbols. Solution The electron experiences an electrostatic force of attraction because of the proton, and the magnitude of this force is Using this value for the net force, we find This orbital speed is almost five million miles per hour.

Since the electrostatic force depends on the inverse square of the distance between the charges, it becomes larger for smaller distances, such as those involved when a strip of adhesive tape is stuck to a smooth surface. Electrons shift over the small distances between the tape and the surface. As a result, the materials become oppositely charged. Since the distance between the charges is relatively small, the electrostatic force of attraction is large enough to contribute to the adhesive bond. Figure 18.12 shows an image of the sticky surface of a piece of tape after it has been pulled off a metal surface. The image was obtained using an atomic-force microscope and reveals the tiny pits left behind when microscopic portions of the adhesive remain stuck to the metal because of the strong adhesive bonding forces.

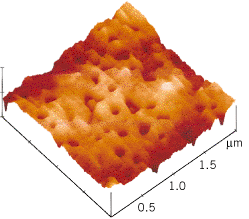Figure 18.12  After a strip of adhesive tape has been pulled off a metal surface, there are tiny pits (approximately one ten-millionth of a meter in diameter) in the sticky surface of the tape, as this image shows. It was obtained using an atomic-force microscope. (Courtesy Louis Scudiero and J. Thomas Dickinson, Washington State University.)

THE FORCE ON A POINT CHARGE DUE TO TWO OR MORE OTHER POINT CHARGES

Up to now, we have been discussing the electrostatic force on a point charge (magnitude |q₁|) due to another point charge (magnitude |q₂|). Suppose that a third point charge (magnitude |q₃|) is also present. What would be the net force on q₁ due to both q₂ and q₃? It is convenient to deal with such a problem in parts. First, find the magnitude and direction of the force exerted on q₁ by q₂ (ignoring q₃). Then, determine the force exerted on q₁ by q₃ (ignoring q₂). The net force on q₁ is the vector sum of these forces. Examples 4 and 5 illustrate this approach when the charges lie along a straight line and on a plane, respectively.

Figure 18.13a shows three point charges that lie along the x axis in a vacuum. Determine the magnitude and direction of the net electrostatic force on q1. 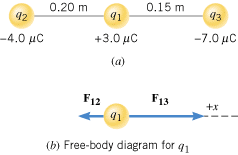Figure 18.13  (a) Three charges lying along the x axis. (b) The force exerted on q1 by q2 is F12, while the force exerted on q1 by q3 is F13. Reasoning  Part b of the drawing shows a free-body diagram of the forces that act on q1. Since q1 and q2 have opposite signs, they attract one another. Thus, the force exerted on q1 by q2 is F12, and it points to the left. Similarly, the force exerted on q1 by q3 is F13 and is also an attractive force. It points to the right in Figure 18.13b. The magnitudes of these forces can be obtained from Coulomb’s law. The net force is the vector sum of F12 and F13. Solution The magnitudes of the forces are Since F12 points in the negative x direction, and F13 points in the positive x direction, the net force F is The plus sign in the answer indicates that the net force points to the right in the drawing.

Interactive LearningWare 18.2 A positive charge is placed on the x axis (q=+7.00 mC, x=0.600 m), and another positive charge is placed on the y axis (q=+9.00 mC, y=0.400 m). A third charge (q=–6.00 mC, m=5.00×10–8 kg) is placed at the coordinate origin. If the charge at the origin were free to move, what would be the magnitude of its acceleration? Related Homework: Problem 18

Figure 18.14a shows three point charges that lie in the x, y plane in a vacuum. Find the magnitude and direction of the net electrostatic force on q1. Figure 18.14  (a) Three charges lying in a plane. (b) The net force acting on q1 is F=F12+F13. The angle that F makes with the +x axis is q . Reasoning  The force exerted on q1 by q2 is F12 and is an attractive force because the two charges have opposite signs. It points along the line between the charges. The force exerted on q1 by q3 is F13 and is also an attractive force. It points along the line between q1 and q3. Coulomb’s law specifies the magnitudes of these forces. Since the forces point in different directions (see Figure 18.14b), we will use vector components to find the net force. Problem solving insight The electrostatic force is a vector and has a direction as well as a magnitude. When adding electrostatic forces, take into account the directions of all forces, using vector components as needed. Solution The magnitudes of the forces are The net force F is the vector sum of F12 and F13, as part b of the drawing shows. The components of F that lie in the x and y directions are Fx and Fy, respectively. Our approach to finding F is the same as that used in Chapters 1 and 4. The forces F12 and F13 are resolved into x and y components. Then, the x components are combined to give Fx, and the y components are combined to give Fy. Once Fx and Fy are known, the magnitude and direction of F can be determined using trigonometry.  Force   x component   y component   F12   +(9.6 N) cos 73°=+2.8 N   +(9.6 N) sin 73°=+9.2 N   F13   +18 N   0 N   F   Fx=+21 N   Fy=+9.2 N  The magnitude F and the angle q  of the net force are

Concept Simulation 18.1

This simulation allows you to change the magnitude and algebraic sign of each charge in Figure 18.14. The forces acting on charge q1 and the resultant of these forces are displayed to scale as changes are made, so that you can see the effects of your choices. Related Homework: Problem 61

The drawing shows three point charges arranged in different ways. The charges are +q, –q, and –q; each has the same magnitude, one being positive and the other two negative. In each part of the drawing the distance d is the same. Rank the arrangements in descending order (largest first) according to the magnitude of the net electrostatic force that acts on the positive charge. Background: The electrostatic force that one point charge exerts on another is described by Coulomb’s law. Like any force, this force is a vector quantity, and the rules of vector addition apply. For similar questions (including calculational counterparts), consult Self-Assessment Test 18.1, which is described next.

Test your understanding of the material in Sections 18.1, 18.2, 18.3, 18.4 and 18.5: · The Origin of Electricity  · Conductors and Insulators   · Charging by Contact and by Induction  · Coulomb’s Law

Copyright © 2000-2003 by John Wiley & Sons, Inc. or related companies. All rights reserved.