30.5.
The Quantum Mechanical Picture of the Hydrogen Atom
The picture of the hydrogen atom that quantum mechanics and the Schrödinger equation provide differs in a number of ways from the Bohr model. The Bohr model uses a single integer number n to identify the various electron orbits and the associated energies. Because this number can have only discrete values, rather than a continuous range of values, n is called a quantum number. In contrast, quantum mechanics reveals that four different quantum numbers are needed to describe each state of the hydrogen atom. These four are described below.
| | 1. |
The principal quantum number n. As in the Bohr model, this number determines the total energy of the atom and can have only integer values: n = = 1, 2, 3, …. In fact, the Schrödinger equation predicts
that the energy of the hydrogen atom is identical to the energy obtained from the Bohr model: E
n 1, 2, 3, …. In fact, the Schrödinger equation predicts
that the energy of the hydrogen atom is identical to the energy obtained from the Bohr model: E
n
 =
=
 –(13.6 eV) Z
2/n
2.
–(13.6 eV) Z
2/n
2.
|
| | 2. |
The orbital quantum number  . This number determines the angular momentum of the electron due to its orbital motion. The values that . This number determines the angular momentum of the electron due to its orbital motion. The values that  can have depend on the value of n, and only the following integers are allowed:
For instance, if n can have depend on the value of n, and only the following integers are allowed:
For instance, if n = = 1, the orbital quantum number can have only the value 1, the orbital quantum number can have only the value   = = 0, but if n 0, but if n = = 4, the values 4, the values   = = 0, 1, 2, and 3 are possible. The magnitude L of the angular momentum of the electron is 0, 1, 2, and 3 are possible. The magnitude L of the angular momentum of the electron is
 | (30.15) |  |
|
| | 3. |
The magnetic quantum number m . The word “magnetic” is used here because an externally applied magnetic field influences the energy of the atom, and this quantum number is used in describing the effect. Since the effect was discovered by the Dutch physicist Pieter Zeeman (1865–1943), it is known as the Zeeman effect. When there is no external magnetic field, m . The word “magnetic” is used here because an externally applied magnetic field influences the energy of the atom, and this quantum number is used in describing the effect. Since the effect was discovered by the Dutch physicist Pieter Zeeman (1865–1943), it is known as the Zeeman effect. When there is no external magnetic field, m plays no role in determining the energy. In either event, the magnetic quantum number determines the component of the angular momentum along a specific direction, which is called the z direction by convention. The values that m plays no role in determining the energy. In either event, the magnetic quantum number determines the component of the angular momentum along a specific direction, which is called the z direction by convention. The values that m can have depend on the value of can have depend on the value of  , with only the following positive and negative integers being permitted:
For example, if the orbital quantum number is , with only the following positive and negative integers being permitted:
For example, if the orbital quantum number is   = = 2, then the magnetic quantum number can have the values m 2, then the magnetic quantum number can have the values m  = = –2, –1, 0, –1, and +2. The component Lz of the angular momentum in the z direction is –2, –1, 0, –1, and +2. The component Lz of the angular momentum in the z direction is
 | (30.16) |  |
|
| | 4. |
The spin quantum number ms. This number is needed because the electron has an intrinsic property called spin angular momentum. Loosely speaking, we can view the electron as spinning while it orbits the nucleus, analogous to the way the earth spins as it orbits the sun. There are two possible values for the spin quantum number of the electron:
Sometimes the phrases “spin up” and “spin down” are used to refer to the directions of the spin angular momentum associated with the values for ms.
|
Table 30.1 summarizes the four quantum numbers that are needed to describe each state of the hydrogen atom. One set of values for n,  , m
, m , and ms corresponds to one state. As the principal quantum number n increases, the number of possible combinations of the four quantum numbers rises rapidly, as Example 5 illustrates.
, and ms corresponds to one state. As the principal quantum number n increases, the number of possible combinations of the four quantum numbers rises rapidly, as Example 5 illustrates.
| Table 30.1
Quantum Numbers for the Hydrogen Atom |
|
Name
|
Symbol
|
Allowed Values
| |
Principal quantum number
|
n
|
1, 2, 3, . . .
|
Orbital quantum number
|

|
0, 1, 2, . . . , (n – – 1) 1)
|
Magnetic quantum number
|
m
|
– , . . . , –2, –1, 0, +1, +2, . . . , + , . . . , –2, –1, 0, +1, +2, . . . , +
|
Spin quantum number
|
ms
|
 , , 
|
|
|
| Example 5 Quantum Mechanical States of the Hydrogen Atom |
 |
|
Determine the number of possible states for the hydrogen atom when the principal quantum number is (a) n = = 1 and (b) n 1 and (b) n = = 2. 2.
Reasoning
Each different combination of the four quantum numbers summarized in Table 30.1 corresponds to a different state. We begin with the value for n and find the allowed values for  . Then, for each . Then, for each  value we find the possibilities for m value we find the possibilities for m . Finally, ms may be . Finally, ms may be  or or  for each group of values for n, for each group of values for n,  , and m , and m . .
Solution
| (a) |
The diagram below shows the possibilities for  , m , m , and ms when n , and ms when n = = 1:
Thus, there are two different states for the hydrogen atom. In the absence of an external magnetic field, these two states have the same energy, since they have the same value of n. 1:
Thus, there are two different states for the hydrogen atom. In the absence of an external magnetic field, these two states have the same energy, since they have the same value of n.
| | (b) |
When n = = 2, there are eight possible combinations for the values of n, 2, there are eight possible combinations for the values of n,  , m , m , and ms, as the diagram below indicates:
With the same value of n , and ms, as the diagram below indicates:
With the same value of n = = 2, all eight states have the same energy when there is no external magnetic field. 2, all eight states have the same energy when there is no external magnetic field.
|
|
 |
Quantum mechanics provides a more accurate picture of atomic structure than does the Bohr model. It is important to realize that the two pictures differ substantially, as Conceptual Example 6 illustrates.
| Conceptual Example 6 The Bohr Model Versus Quantum Mechanics |
 |
|
Consider two hydrogen atoms. There are no external magnetic fields present, and the electron in each atom has the same energy. According to the Bohr model and to quantum mechanics, is it possible for the electrons in these atoms (a) to have zero orbital angular momentum and (b) to have different orbital angular momenta?
Reasoning and Solution
| (a) |
In both the Bohr model and quantum mechanics, the energy is proportional to 1/n2, according to Equation 30.13, where n is the principal quantum number. Moreover, the value of n may be n = = 1, 2, 3, … , and may not be zero. In the Bohr model, the fact that n may not be zero means that it is not possible for the orbital angular momentum to be zero because the angular momentum is proportional to n, according to Equation 30.8. In the quantum mechanical picture the magnitude of the orbital angular momentum is proportional to 1, 2, 3, … , and may not be zero. In the Bohr model, the fact that n may not be zero means that it is not possible for the orbital angular momentum to be zero because the angular momentum is proportional to n, according to Equation 30.8. In the quantum mechanical picture the magnitude of the orbital angular momentum is proportional to  , as given by Equation 30.15. Here, , as given by Equation 30.15. Here,  is the orbital quantum number and may take on the values is the orbital quantum number and may take on the values   = = 0, 1, 2, … , (n 0, 1, 2, … , (n – – 1). We note that 1). We note that  [and therefore [and therefore  ] may be zero, no matter what the value for n is. Consequently, the orbital angular momentum may be zero according to quantum mechanics, in contrast to the case for the Bohr model. ] may be zero, no matter what the value for n is. Consequently, the orbital angular momentum may be zero according to quantum mechanics, in contrast to the case for the Bohr model.
| | (b) |
If the electrons have the same energy, they have the same value for the principal quantum number n. In the Bohr model, this means that they cannot have different values for the orbital angular momentum Ln, since Ln = = nh/(2p), according to Equation 30.8. In quantum mechanics, the energy is also determined by n when external magnetic fields are absent, but the orbital angular momentum is determined by nh/(2p), according to Equation 30.8. In quantum mechanics, the energy is also determined by n when external magnetic fields are absent, but the orbital angular momentum is determined by  . Since . Since   = = 0, 1, 2, … , (n 0, 1, 2, … , (n – – 1), different values of 1), different values of  are compatible with the same value of n. For instance, if n are compatible with the same value of n. For instance, if n = = 2 for both electrons, one of them could have 2 for both electrons, one of them could have   = = 0, while the other could have 0, while the other could have   = = 1. According to quantum mechanics, then, the electrons could have different orbital angular momenta, even though they have the same energy. 1. According to quantum mechanics, then, the electrons could have different orbital angular momenta, even though they have the same energy.
|
Reasoning and Solution The following table summarizes the discussion from parts (a) and (b):
|
Bohr Model
|
Quantum Mechanics
| |
(a) For a given n, can the angular momentum ever be zero?
|
No
|
Yes
|
(b) For a given n, can the angular momentum have different values?
|
No
|
Yes
|
|
Related Homework:
Conceptual Question 5
, Problem 26
|
 |
According to the Bohr model, the nth orbit is a circle of radius rn, and every time the position of the electron in this orbit is measured, the electron is found exactly at a distance rn away from the nucleus. This simplistic picture is now known to be incorrect, and the quantum mechanical picture of the atom has replaced it. Suppose the electron is in a quantum mechanical state for which n =
= 1, and we imagine making a number of measurements of the electron’s position with respect to the nucleus. We would find that its position is uncertain, in the sense that there is a probability of finding the electron sometimes very near the nucleus, sometimes very far from the nucleus, and sometimes at intermediate locations. The probability is determined by the wave function Y, as Section 29.5 discusses. We can make a three-dimensional picture of our findings by marking a dot at each location where the electron is found. More dots occur at places where the probability of finding the electron is higher, and after a sufficient number of measurements, a picture of the quantum mechanical state emerges. Figure 30.13 shows the spatial distribution for an electron in a state for which n
1, and we imagine making a number of measurements of the electron’s position with respect to the nucleus. We would find that its position is uncertain, in the sense that there is a probability of finding the electron sometimes very near the nucleus, sometimes very far from the nucleus, and sometimes at intermediate locations. The probability is determined by the wave function Y, as Section 29.5 discusses. We can make a three-dimensional picture of our findings by marking a dot at each location where the electron is found. More dots occur at places where the probability of finding the electron is higher, and after a sufficient number of measurements, a picture of the quantum mechanical state emerges. Figure 30.13 shows the spatial distribution for an electron in a state for which n =
= 1,
1, 
 =
= 0, and m
0, and m
 =
= 0. This picture is constructed from so many measurements that the individual dots are no longer visible but have merged to form a kind of probability “cloud” whose density changes gradually from place to place. The dense regions indicate places where the probability of finding the electron is higher, and the less dense regions indicate places where the probability is lower. Also indicated in Figure 30.13 is the radius where quantum mechanics predicts the greatest probability per unit radial distance of finding the electron in the n
0. This picture is constructed from so many measurements that the individual dots are no longer visible but have merged to form a kind of probability “cloud” whose density changes gradually from place to place. The dense regions indicate places where the probability of finding the electron is higher, and the less dense regions indicate places where the probability is lower. Also indicated in Figure 30.13 is the radius where quantum mechanics predicts the greatest probability per unit radial distance of finding the electron in the n =
= 1 state. This radius matches exactly the radius of
1 state. This radius matches exactly the radius of  found for the first Bohr orbit.
found for the first Bohr orbit.
 | Figure 30.13
The electron probability cloud for the ground state (n
 =
=
 1, 1, 
 =
=
 0, m 0, m

 =
=
 0) of the hydrogen atom. 0) of the hydrogen atom. |
|
For a principal quantum number of n =
= 2, the probability clouds are different than for n
2, the probability clouds are different than for n =
= 1. In fact, more than one cloud shape is possible because with n
1. In fact, more than one cloud shape is possible because with n =
= 2 the orbital quantum number can be either
2 the orbital quantum number can be either 
 =
= 0 or
0 or 
 =
= 1. Although the value of
1. Although the value of  does not affect the energy of the hydrogen atom, the value does have a significant effect on the shape of the probability clouds. Figure 30.14a shows the cloud for n
does not affect the energy of the hydrogen atom, the value does have a significant effect on the shape of the probability clouds. Figure 30.14a shows the cloud for n =
= 2,
2, 
 =
= 0, and m
0, and m
 =
= 0. Part b of the drawing shows that when n
0. Part b of the drawing shows that when n =
= 2,
2, 
 =
= 1, and m
1, and m
 =
= 0, the cloud has a two-lobe shape with the nucleus at the center between the lobes. For larger values of n, the probability clouds become increasingly complex and are spread out over larger volumes of space.
0, the cloud has a two-lobe shape with the nucleus at the center between the lobes. For larger values of n, the probability clouds become increasingly complex and are spread out over larger volumes of space.
 | Figure 30.14
The electron probability clouds for the hydrogen atom when (a) n
 =
=
 2, 2, 
 =
=
 0, m 0, m

 =
=
 0 and (b) n 0 and (b) n
 =
=
 2, 2, 
 =
=
 1, m 1, m

 =
=
 0. 0. |
|
The probability cloud picture of the electron in a hydrogen atom is very different from the well-defined orbit of the Bohr model. The fundamental reason for this difference is to be found in the Heisenberg uncertainty principle, as Conceptual Example 7 discusses.
| Conceptual Example 7 The Uncertainty Principle and the Hydrogen Atom |
 |
|
In the Bohr model of the hydrogen atom, the electron in the ground state (n = = 1) is in an orbit that has a radius of exactly 1) is in an orbit that has a radius of exactly  . Furthermore, as calculated in Example 18.3, the speed of the electron in this orbit is exactly 2.18 . Furthermore, as calculated in Example 18.3, the speed of the electron in this orbit is exactly 2.18 × × 106 m/s. Considering the Heisenberg uncertainty principle, is this a realistic picture of atomic structure? 106 m/s. Considering the Heisenberg uncertainty principle, is this a realistic picture of atomic structure?
Reasoning and Solution The Bohr model indicates that the electron is located exactly at a radius of  , so the uncertainty Dy in its radial position is zero. We will now show that an uncertainty of Dy , so the uncertainty Dy in its radial position is zero. We will now show that an uncertainty of Dy = = 0 m is not consistent with the Heisenberg principle, so that the Bohr picture is not realistic. What does the Heisenberg principle [Equation 29.10, (Dpy)(Dy) 0 m is not consistent with the Heisenberg principle, so that the Bohr picture is not realistic. What does the Heisenberg principle [Equation 29.10, (Dpy)(Dy) 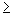  h/(4p)] say about Dy? According to the principle, the minimum uncertainty in the radial position of the electron is Dy h/(4p)] say about Dy? According to the principle, the minimum uncertainty in the radial position of the electron is Dy = = h/(4p Dpy), where Dpy is the uncertainty in the momentum. The magnitude of the electron’s momentum is the product of its mass m and speed v, so that Dpy h/(4p Dpy), where Dpy is the uncertainty in the momentum. The magnitude of the electron’s momentum is the product of its mass m and speed v, so that Dpy = = D(mv) D(mv) = = m Dv. It seems reasonable to assume that the uncertainty Dv in the speed should be less than 2.18 m Dv. It seems reasonable to assume that the uncertainty Dv in the speed should be less than 2.18 × × 106 m/s. This means that the speed is somewhere between zero and twice the value known to apply to the ground state in the Bohr model. A much larger uncertainty would mean that the electron could have so much energy that it would not likely remain in orbit. With Dv 106 m/s. This means that the speed is somewhere between zero and twice the value known to apply to the ground state in the Bohr model. A much larger uncertainty would mean that the electron could have so much energy that it would not likely remain in orbit. With Dv = = 2.18 2.18 × × 106 m/s and 106 m/s and  for the mass of the electron, we find that the minimum uncertainty in the radial position of the electron is for the mass of the electron, we find that the minimum uncertainty in the radial position of the electron is  . This uncertainty is quite large, because it is about one-half of the Bohr radius. According to the uncertainty principle, then, the radial position of the electron can be anywhere from approximately one-half to one and a half times the Bohr radius. The single-radius orbit of the Bohr model does not correctly represent this aspect of reality at the atomic level. Quantum mechanics, however, does correctly represent it in terms of a probability cloud picture of atomic structure. . This uncertainty is quite large, because it is about one-half of the Bohr radius. According to the uncertainty principle, then, the radial position of the electron can be anywhere from approximately one-half to one and a half times the Bohr radius. The single-radius orbit of the Bohr model does not correctly represent this aspect of reality at the atomic level. Quantum mechanics, however, does correctly represent it in terms of a probability cloud picture of atomic structure.
|
 |
| Check Your Understanding 2 |
 |
|
The magnitude of the orbital angular momentum of the electron in a hydrogen atom is observed to increase. Does this necessarily mean that the energy of the electron also increases? Answer this question from the point of view of (a) the Bohr model and (b) the quantum mechanical picture of the hydrogen atom.
Background:
Both the Bohr model of the hydrogen atom and the quantum mechanical picture of the hydrogen atom predict the same energy levels for the electron in the atom. In other respects, however, these two approaches differ in what they have to say about the hydrogen atom.
For similar questions (including calculational counterparts), consult Self-Assessment Test 30.1, which is described next.
|
|
 |
| Self-Assessment Test 30.1 |
 |
|
Test your understanding of the material in Sections 30.1, 30.2, 30.3, 30.4 and 30.5:
· The Nuclear Atom · Line Spectra · The Bohr Model of the Hydrogen Atom · De Broglie’s Explanation of Bohr’s Assumption about Angular Momentum · The Quantum Mechanical Picture of the Hydrogen Atom
|
|
 |
 |
| Copyright © 2000-2003 by John Wiley & Sons, Inc. or related companies. All rights reserved. |
 . This number determines the angular momentum of the electron due to its orbital motion. The values that
. This number determines the angular momentum of the electron due to its orbital motion. The values that  can have depend on the value of n, and only the following integers are allowed:
can have depend on the value of n, and only the following integers are allowed:




 . The word “magnetic” is used here because an externally applied magnetic field influences the energy of the atom, and this quantum number is used in describing the effect. Since the effect was discovered by the Dutch physicist Pieter Zeeman (1865–1943), it is known as the Zeeman effect. When there is no external magnetic field, m
. The word “magnetic” is used here because an externally applied magnetic field influences the energy of the atom, and this quantum number is used in describing the effect. Since the effect was discovered by the Dutch physicist Pieter Zeeman (1865–1943), it is known as the Zeeman effect. When there is no external magnetic field, m plays no role in determining the energy. In either event, the magnetic quantum number determines the component of the angular momentum along a specific direction, which is called the z direction by convention. The values that m
plays no role in determining the energy. In either event, the magnetic quantum number determines the component of the angular momentum along a specific direction, which is called the z direction by convention. The values that m can have depend on the value of
can have depend on the value of  , with only the following positive and negative integers being permitted:
, with only the following positive and negative integers being permitted:





 ,
, 
 or
or  for each group of values for
for each group of values for 

 , as given by Equation 30.15. Here,
, as given by Equation 30.15. Here,  ] may be zero, no matter what the value for
] may be zero, no matter what the value for  found for the first Bohr orbit.
found for the first Bohr orbit.

 . Furthermore, as calculated in Example 18.3, the speed of the electron in this orbit is exactly 2.18
. Furthermore, as calculated in Example 18.3, the speed of the electron in this orbit is exactly 2.18 , so the uncertainty
, so the uncertainty 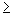
 for the mass of the electron, we find that the minimum uncertainty in the radial position of the electron is
for the mass of the electron, we find that the minimum uncertainty in the radial position of the electron is  . This uncertainty is quite large, because it is about one-half of the Bohr radius. According to the uncertainty principle, then, the radial position of the electron can be anywhere from approximately one-half to one and a half times the Bohr radius. The single-radius orbit of the Bohr model does not correctly represent this aspect of reality at the atomic level. Quantum mechanics, however, does correctly represent it in terms of a probability cloud picture of atomic structure.
. This uncertainty is quite large, because it is about one-half of the Bohr radius. According to the uncertainty principle, then, the radial position of the electron can be anywhere from approximately one-half to one and a half times the Bohr radius. The single-radius orbit of the Bohr model does not correctly represent this aspect of reality at the atomic level. Quantum mechanics, however, does correctly represent it in terms of a probability cloud picture of atomic structure.