| Equilibrium Applications of Newton’s Laws of Motion |
|
|  |
Have you ever been so upset that it took days to recover your “equilibrium?” In this context, the word “equilibrium” refers to a balanced state of mind, one that is not changing wildly. In physics, the word “equilibrium” also refers to a lack of change, but in the sense that the velocity of an object isn’t changing. If its velocity doesn’t change, an object is not accelerating. Our definition of equilibrium, then, is as follows:
| Definition of Equilibrium |
| * An object is in equilibrium when it has zero acceleration. |
 | Concepts at a Glance |
 |
The concept of equilibrium arises directly from Newton’s second law. The Concepts-at-a-Glance chart in Figure 4-28, which is an enhanced version of the chart in Figure 4-9, illustrates this important point. When the acceleration of an object is zero (
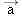
= 0 m/s
2), the object is in equilibrium, as the upper-right part of the chart indicates. This section presents several examples involving equilibrium situations. On the other hand, when the acceleration is not zero (
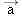
≠ 0 m/s
2), we have a non-equilibrium situation, as the lower-right part of the chart suggests. Section 4.12 deals with nonequilibrium applications of Newton’s second law.
 |  | |  | Figure 4-28 CONCEPTS AT A GLANCE Both equilibrium and nonequilibrium problems can be solved with the aid of Newton’s second law. For equilibrium situations, such as the gymnast holding the “Iron Cross” position in the left photograph, the acceleration is zero (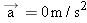 ). For nonequilibrium situations, such as the freely falling gymnast in the right photograph, the acceleration is not zero ( ). For nonequilibrium situations, such as the freely falling gymnast in the right photograph, the acceleration is not zero (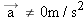 ). (© Both, Mike Powell/Allsport/Getty Images). ). (© Both, Mike Powell/Allsport/Getty Images).
|
|  |
|  |
 |  | |  | Figure 4-29 (a) A traction device for the foot. (b) The free-body diagram for the pulley on the foot.
|
|  |
|  |
Since the acceleration is zero for an object in equilibrium, all of the acceleration components are also zero. In two dimensions, this means that
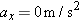
and

. Substituting these values into the second law (
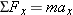
and
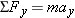
) shows that the
x component and the
y component of the net force must each be zero. In other words, the forces acting on an object in equilibrium must balance. Thus, in two dimensions, the equilibrium condition is expressed by two equations:
In using Equations 4.9a and 4.9b to solve equilibrium problems, we will use the following five-step reasoning strategy:
 |
 | | BOX 4.1 | Reasoning Strategy |
Analyzing Equilibrium Situations
 |
1. | Select the object (often called the “system”) to which Equations 4.9a and 4.9b are to be applied. It may be that two or more objects are connected by means of a rope or a cable. If so, it may be necessary to treat each object separately according to the following steps. |  |
2. | Draw a free-body diagram for each object chosen above. Be sure to include only forces that act on the object. Do not include forces that the object exerts on its environment. |  |
3. | Choose a set of x, y axes for each object and resolve all forces in the free-body diagram into components that point along these axes. Select the axes so that as many forces as possible point along the x axis or the y axis. Such a choice minimizes the calculations needed to determine the force components. |  |
4. | Apply Equations 4.9a and 4.9b by setting the sum of the x components and the sum of the y components of the forces each equal to zero. |  |
5. | Solve the two equations obtained in Step 4 for the desired unknown quantities, remembering that two equations can yield answers for only two unknowns at most. |  |
|
|
|  |
 |
Example 11 illustrates how these steps are followed. It deals with a traction device in which three forces act together to bring about the equilibrium.

| Example 11 | | | Traction for the Foot |
|
Figure 4-29 a shows a traction device used with a foot injury. The weight of the 2.2-kg object creates a tension in the rope that passes around the pulleys. Therefore, tension forces 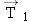 and  are applied to the pulley on the foot. It may seem surprising that the rope applies a force to either side of the foot pulley. A similar effect occurs when you place a finger inside a rubber band and push downward. You can feel each side of the rubber band pulling upward on the finger. The foot pulley is kept in equilibrium because the foot also applies a force 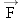 to it. This force arises in reaction (Newton’s third law) to the pulling effect of the forces 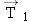 and  . Ignoring the weight of the foot, find the magnitude of 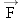 .
Reasoning The forces 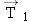 ,  , and 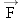 keep the pulley on the foot at rest. The pulley, therefore, has no acceleration and is in equilibrium. As a result, the sum of the x components and the sum of the y components of the three forces must each be zero. Figure 4-29 b shows the free-body diagram of the pulley on the foot. The x axis is chosen to be along the direction of force 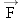 , and the components of the forces are indicated in the drawing. (See Section 1.7 for a review of vector components.)
Solution Since the sum of the y components of the forces is zero, it follows that
or 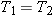 . In other words, the magnitudes of the tension forces are equal. In addition, the sum of the x components of the forces is zero, so we have that
Solving for F and letting 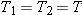 , we find that  . However, the tension T in the rope is determined by the weight of the 2.2-kg object: 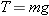 , where m is its mass and g is the acceleration due to gravity. Therefore, the magnitude of 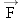 is
|
 |
Problem solving insight Choose the orientation of the x, y axes for convenience. In Example 11, the axes have been rotated so the force 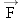 points along the x axis. Since points along the x axis. Since 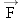 does not have a component along the y axis, the analysis is simplified. does not have a component along the y axis, the analysis is simplified. |
Example 12 presents another situation in which three forces are responsible for the equilibrium of an object. However, in this example all the forces have different magnitudes.

| Example 12 | | | Replacing an Engine |
|
An automobile engine has a weight  , whose magnitude is W = 3150 N. This engine is being positioned above an engine compartment, as Figure 4-30 a illustrates. To position the engine, a worker is using a rope. Find the tension 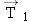 in the supporting cable and the tension  in the positioning rope.
Reasoning Under the influence of the forces 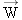 , 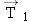 , and  the ring in Figure 4-30 a is at rest and, therefore, in equilibrium. Consequently, the sum of the x components and the sum of the y components of these forces must each be zero;  and 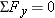 . By using these relations, we can find T1 and T2. Figure 4-30 b shows the free-body diagram of the ring and the force components for a suitable x, y axis system.
Solution The free-body diagram shows the components for each of the three forces, and the components are listed in the following table:
Force | x Component | y Component | | −T1 sin 10.0° | +T1 cos 10.0° | | +T2 sin 80.0° | −T2 cos 80.0° | | 0 | −W |
|
The plus signs in the table denote components that point along the positive axes, and the minus signs denote components that point along the negative axes. Setting the sum of the x components and the sum of the y components equal to zero leads to the following equations:
Solving the first of these equations for T1 shows that
Substituting this expression for T1 into the second equation gives
Setting W = 3150 N in this result yields  .
Since 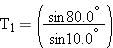 T 2 and T 2 = 582 N, it follows that  . |
 |
Problem solving insight When an object is in equilibrium, as here in Example 12, the net force is zero, 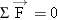 . This does not mean that each individual force is zero. It means that the vector sum of all the forces is zero. . This does not mean that each individual force is zero. It means that the vector sum of all the forces is zero. |
An object can be moving and still be in equilibrium, provided there is no acceleration. Example 13 illustrates such a case, and the solution is again obtained using the fivestep reasoning strategy summarized at the beginning of the section.

| Example 13 | | | Equilibrium at Constant Velocity |
|
A jet plane is flying with a constant speed along a straight line, at an angle of 30.0° above the horizontal, as Figure 4-31 a indicates. The plane has a weight 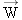 whose magnitude is W = 86 500 N, and its engines provide a forward thrust 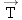 of magnitude T = 103 000 N. In addition, the lift force  (directed perpendicular to the wings) and  the force of air resistance (directed opposite to the motion) act on the plane. Find  and  .  |  | |  | Figure 4-30 (a) The ring is in equilibrium because of the three forces 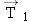 (the tension force in the supporting cable), (the tension force in the supporting cable),  (the tension force in the positioning rope), and (the tension force in the positioning rope), and  (the weight of the engine). (b) The free-body diagram for the ring. (the weight of the engine). (b) The free-body diagram for the ring.
|
|  |
|  |
 |  | |  | Figure 4-31 (a) A plane moves with a constant velocity at an angle of 30.0° above the horizontal due to the action of four forces, the weight  , the lift , the lift  , the engine thrust , the engine thrust  , and the air resistance , and the air resistance  . (b) The free-body diagram for the plane. (c) This geometry occurs often in physics. . (b) The free-body diagram for the plane. (c) This geometry occurs often in physics.
|
|  |
|  |
Reasoning Figure 4-31 b shows the free-body diagram of the plane, including the forces  ,  ,  , and  . Since the plane is not accelerating, it is in equilibrium, and the sum of the x components and the sum of the y components of these forces must be zero. The lift force  and the force  of air resistance can be obtained from these equilibrium conditions. To calculate the components, we have chosen axes in the free-body diagram that are rotated by 30.0° from their usual horizontal-vertical positions. This has been done purely for convenience, since the weight  is then the only force that does not lie along either axis.
Problem solving insight A moving object is in equilibrium if it moves with a constant velocity; then its acceleration is zero. A zero acceleration is the fundamental characteristic of an object in equilibrium. |
Solution When determining the components of the weight, it is necessary to realize that the angle  in Figure 4-31 a is 30.0°. Part c of the drawing focuses attention on the geometry that is responsible for this fact. There it can be seen that  and  , with the result that 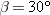 . The table below lists the components of the forces that act on the jet.
Force | x Component | y Component |
| − W sin 30.0° | − W cos 30.0° | | 0 | + L | | + T | 0 | | − R | 0 |
|
Setting the sum of the x component of the forces to zero gives
Setting the sum of the y component of the forces to zero gives
|
 |
Need more practice?
 |
 | | Interactive LearningWare4.3 | |
A 0.600-kg kite is being flown at the end of a string. The string is straight and makes an angle of 55.0° above the horizontal. The kite is stationary, and the tension in the string is 35.0 N. Determine the force (both magnitude and direction) that the wind exerts on the kite. Specify the angle relative to the horizontal.
Related Homework: Problems 46, 56
|
|
 Check Your Understanding 4 Check Your Understanding 4 |
In which one of the following situations could an object possibly be in equilibrium? (a) Three forces act on the object. The forces all point along the same line but may have different directions. (b) Two perpendicular forces act on the object. (c) A single force acts on the object. (d) In none of the situations described in (a), (b), and (c) could the object possibly be in equilibrium. (The answer is given at the end of the book.)
Background: A number of concepts enter the picture here: force, net force, and equilibrium. The addition of vectors also plays a role, as does Newton’s second law of motion.
For similar questions (including calculational counterparts), consult Self-Assessment Test 4.3. This test is described at the end of Section 4.12. |
 |
| Copyright © 2007 John Wiley & Sons, Inc. All rights reserved. |
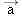 = 0 m/s2), the object is in equilibrium, as the upper-right part of the chart indicates. This section presents several examples involving equilibrium situations. On the other hand, when the acceleration is not zero (
= 0 m/s2), the object is in equilibrium, as the upper-right part of the chart indicates. This section presents several examples involving equilibrium situations. On the other hand, when the acceleration is not zero (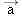 ≠ 0 m/s2), we have a non-equilibrium situation, as the lower-right part of the chart suggests. Section 4.12 deals with nonequilibrium applications of Newton’s second law.
≠ 0 m/s2), we have a non-equilibrium situation, as the lower-right part of the chart suggests. Section 4.12 deals with nonequilibrium applications of Newton’s second law.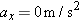 and
and  . Substituting these values into the second law (
. Substituting these values into the second law (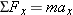 and
and 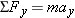 ) shows that the x component and the y component of the net force must each be zero. In other words, the forces acting on an object in equilibrium must balance. Thus, in two dimensions, the equilibrium condition is expressed by two equations:
) shows that the x component and the y component of the net force must each be zero. In other words, the forces acting on an object in equilibrium must balance. Thus, in two dimensions, the equilibrium condition is expressed by two equations:
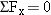
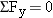
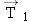 and
and  are applied to the pulley on the foot. It may seem surprising that the rope applies a force to either side of the foot pulley. A similar effect occurs when you place a finger inside a rubber band and push downward. You can feel each side of the rubber band pulling upward on the finger. The foot pulley is kept in equilibrium because the foot also applies a force
are applied to the pulley on the foot. It may seem surprising that the rope applies a force to either side of the foot pulley. A similar effect occurs when you place a finger inside a rubber band and push downward. You can feel each side of the rubber band pulling upward on the finger. The foot pulley is kept in equilibrium because the foot also applies a force 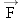 to it. This force arises in reaction (Newton’s third law) to the pulling effect of the forces
to it. This force arises in reaction (Newton’s third law) to the pulling effect of the forces 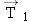 and
and  . Ignoring the weight of the foot, find the magnitude of
. Ignoring the weight of the foot, find the magnitude of 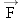 .
.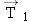 ,
,  , and
, and 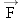 keep the pulley on the foot at rest. The pulley, therefore, has no acceleration and is in equilibrium. As a result, the sum of the x components and the sum of the y components of the three forces must each be zero. Figure 4-29b shows the free-body diagram of the pulley on the foot. The x axis is chosen to be along the direction of force
keep the pulley on the foot at rest. The pulley, therefore, has no acceleration and is in equilibrium. As a result, the sum of the x components and the sum of the y components of the three forces must each be zero. Figure 4-29b shows the free-body diagram of the pulley on the foot. The x axis is chosen to be along the direction of force 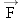 , and the components of the forces are indicated in the drawing. (See Section 1.7 for a review of vector components.)
, and the components of the forces are indicated in the drawing. (See Section 1.7 for a review of vector components.)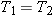 . In other words, the magnitudes of the tension forces are equal. In addition, the sum of the x components of the forces is zero, so we have that
. In other words, the magnitudes of the tension forces are equal. In addition, the sum of the x components of the forces is zero, so we have that
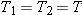 , we find that
, we find that  . However, the tension T in the rope is determined by the weight of the 2.2-kg object:
. However, the tension T in the rope is determined by the weight of the 2.2-kg object: 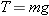 , where m is its mass and g is the acceleration due to gravity. Therefore, the magnitude of
, where m is its mass and g is the acceleration due to gravity. Therefore, the magnitude of 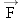 is
is

 , whose magnitude is W = 3150 N. This engine is being positioned above an engine compartment, as Figure 4-30a illustrates. To position the engine, a worker is using a rope. Find the tension
, whose magnitude is W = 3150 N. This engine is being positioned above an engine compartment, as Figure 4-30a illustrates. To position the engine, a worker is using a rope. Find the tension 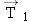 in the supporting cable and the tension
in the supporting cable and the tension  in the positioning rope.
in the positioning rope.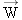 ,
, 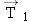 , and
, and  the ring in Figure 4-30a is at rest and, therefore, in equilibrium. Consequently, the sum of the x components and the sum of the y components of these forces must each be zero;
the ring in Figure 4-30a is at rest and, therefore, in equilibrium. Consequently, the sum of the x components and the sum of the y components of these forces must each be zero;  and
and 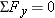 . By using these relations, we can find T1 and T2. Figure 4-30b shows the free-body diagram of the ring and the force components for a suitable x, y axis system.
. By using these relations, we can find T1 and T2. Figure 4-30b shows the free-body diagram of the ring and the force components for a suitable x, y axis system. .
.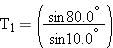 T2 and T2 = 582 N, it follows that
T2 and T2 = 582 N, it follows that  .
.
 whose magnitude is W = 86 500 N, and its engines provide a forward thrust
whose magnitude is W = 86 500 N, and its engines provide a forward thrust  of magnitude T = 103 000 N. In addition, the lift force
of magnitude T = 103 000 N. In addition, the lift force  (directed perpendicular to the wings) and
(directed perpendicular to the wings) and  the force of air resistance (directed opposite to the motion) act on the plane. Find
the force of air resistance (directed opposite to the motion) act on the plane. Find  and
and  .
. ,
,  ,
,  , and
, and  . Since the plane is not accelerating, it is in equilibrium, and the sum of the x components and the sum of the y components of these forces must be zero. The lift force
. Since the plane is not accelerating, it is in equilibrium, and the sum of the x components and the sum of the y components of these forces must be zero. The lift force  and the force
and the force  of air resistance can be obtained from these equilibrium conditions. To calculate the components, we have chosen axes in the free-body diagram that are rotated by 30.0° from their usual horizontal-vertical positions. This has been done purely for convenience, since the weight
of air resistance can be obtained from these equilibrium conditions. To calculate the components, we have chosen axes in the free-body diagram that are rotated by 30.0° from their usual horizontal-vertical positions. This has been done purely for convenience, since the weight  is then the only force that does not lie along either axis.
is then the only force that does not lie along either axis. in Figure 4-31a is 30.0°. Part c of the drawing focuses attention on the geometry that is responsible for this fact. There it can be seen that
in Figure 4-31a is 30.0°. Part c of the drawing focuses attention on the geometry that is responsible for this fact. There it can be seen that  and
and  , with the result that
, with the result that 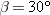 . The table below lists the components of the forces that act on the jet.
. The table below lists the components of the forces that act on the jet.


 Check Your Understanding 4
Check Your Understanding 4