4.12 |
Nonequilibrium Applications of Newton’s Laws of Motion |
|
| ||
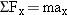
| (4.2a) |
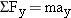
| (4.2b) |
| ||||||||||||||||||||||||||||||||||||||||
|
A supertanker of mass 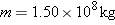 is being towed by two tugboats, as in Figure 4-32a. The tensions in the towing cables apply the forces is being towed by two tugboats, as in Figure 4-32a. The tensions in the towing cables apply the forces 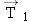 and and  at equal angles of 30.0° with respect to the tanker’s axis. In addition, the tanker’s engines produce a forward drive force at equal angles of 30.0° with respect to the tanker’s axis. In addition, the tanker’s engines produce a forward drive force 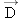 , whose magnitude is , whose magnitude is 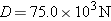 . Moreover, the water applies an opposing force . Moreover, the water applies an opposing force 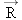 , whose magnitude is , whose magnitude is 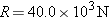 . The tanker moves forward with an acceleration that points along the tanker’s axis and has a magnitude of . The tanker moves forward with an acceleration that points along the tanker’s axis and has a magnitude of 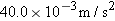 . Find the magnitudes of the tensions . Find the magnitudes of the tensions 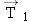 and and  . .
Reasoning The unknown forces 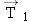 and and  contribute to the net force that accelerates the tanker. To determine contribute to the net force that accelerates the tanker. To determine 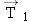 and and  , therefore, we analyze the net force, which we will do using components. The various force components can be found by referring to the free-body diagram for the tanker in Figure 4-32b, where the ship’s axis is chosen as the x axis. We will then use Newton’s second law in its component form, , therefore, we analyze the net force, which we will do using components. The various force components can be found by referring to the free-body diagram for the tanker in Figure 4-32b, where the ship’s axis is chosen as the x axis. We will then use Newton’s second law in its component form, 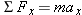 and and 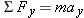 , to obtain the magnitudes of , to obtain the magnitudes of 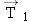 and and  . .Solution The individual force components are summarized as follows:
 ). Consequently, the sum of the y components of the forces must be zero: ). Consequently, the sum of the y components of the forces must be zero:
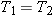 . Since the ship accelerates along the x direction, the sum of the x components of the forces is not zero. The second law indicates that . Since the ship accelerates along the x direction, the sum of the x components of the forces is not zero. The second law indicates that
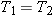 , we can replace the two separate tension symbols by a single symbol T, the magnitude of the tension. Solving for T gives , we can replace the two separate tension symbols by a single symbol T, the magnitude of the tension. Solving for T gives
| ||||||||||||||||||||||||||||||||||||||||
 |
| ||||||||||||||||||||||||||||
|
A truck is hauling a trailer along a level road, as Figure 4-33a illustrates. The mass of the truck is m1 = 8500 kg and that of the trailer is m2 = 27 000 kg. The two move along the x axis with an acceleration of 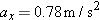 . Ignoring the retarding forces of friction and air resistance, determine (a) the tension . Ignoring the retarding forces of friction and air resistance, determine (a) the tension  in the horizontal drawbar between the trailer and the truck and (b) the force in the horizontal drawbar between the trailer and the truck and (b) the force 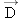 that propels the truck forward. that propels the truck forward.
Reasoning Since the truck and the trailer accelerate along the horizontal direction and friction is being ignored, only forces that have components in the horizontal direction are of interest. Therefore, Figure 4-33 omits the weight and the normal force, which act vertically. To determine the tension force  in the drawbar, we draw the free-body diagram for the trailer and apply Newton’s second law, in the drawbar, we draw the free-body diagram for the trailer and apply Newton’s second law, 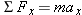 . Similarly, we can determine the propulsion force . Similarly, we can determine the propulsion force 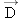 by drawing the free-body diagram for the truck and applying Newton’s second law. by drawing the free-body diagram for the truck and applying Newton’s second law.Solution
| ||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||
|
Figure 4-34 shows a water skier at four different moments:
Reasoning and Solution According to Newton’s second law, if an object has zero acceleration, the net force acting on it is zero. In such a case, the object is in equilibrium. In contrast, if the object has an acceleration, the net force acting on it is not zero. Such an object is not in equilibrium. We will apply this criterion to each of the four phases of the motion to decide whether the net force is zero.
Related Homework: Problem 68
| ||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||
|
Need more practice?
 |
|
A N A L Y Z I N G M U L T I P L E - C O N C E P T P R O B L E M S | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||
|
Block 1 (mass m1 = 8.00 kg) is moving on a frictionless 30.0° incline. This block is connected to block 2 (mass m2 = 22.0 kg) by a massless cord that passes over a massless and frictionless pulley (see Figure 4-36a). Find the acceleration of each block and the tension in the cord.
Reasoning Since both blocks accelerate, there must be a net force acting on each one. The key to this problem is to realize that Newton’s second law can be used separately for each block to relate the net force and the acceleration. Note also that both blocks have accelerations of the same magnitude a, since they move as a unit. We assume that block 1 accelerates up the incline and choose this direction to be the +x axis. If block 1 in reality accelerates down the incline, then the value obtained for the acceleration will be a negative number. Solution Three forces act on block 1: (1) 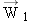 is its weight [ is its weight [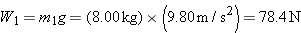 ], (2) ], (2)  is the force applied because of the tension in the cord, and (3) is the force applied because of the tension in the cord, and (3)  is the normal force that the incline exerts. Figure 4-36b shows the free-body diagram for block 1. The weight is the only force that does not point along the x, y axes, and its x and y components are given in the diagram. Applying Newton’s second law ( is the normal force that the incline exerts. Figure 4-36b shows the free-body diagram for block 1. The weight is the only force that does not point along the x, y axes, and its x and y components are given in the diagram. Applying Newton’s second law (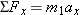 ) to block 1 shows that ) to block 1 shows that
Two forces act on block 2, as the free-body diagram in Figure 4-36b indicates: (1) 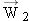 is its weight [ is its weight [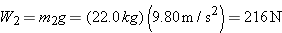 ] and (2) ] and (2) 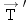 is exerted as a result of block 1 pulling back on the connecting cord. Since the cord and the frictionless pulley are massless, the magnitudes of is exerted as a result of block 1 pulling back on the connecting cord. Since the cord and the frictionless pulley are massless, the magnitudes of 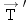 and and 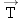 are the same: are the same: 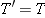 . Applying Newton’s second law ( . Applying Newton’s second law (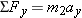 ) to block 2 reveals that ) to block 2 reveals that
| |||||||||||||||||||||
 |
| |||||||||||||||
|
A window washer on a scaffold is hoisting the scaffold up the side of a building by pulling downward on a rope, as in Figure 4-37a. The magnitude of the pulling force is 540 N, and the combined mass of the worker and the scaffold is 155 kg. Find the upward acceleration of the unit.
Reasoning The worker and the scaffold form a single unit, on which the rope exerts a force in three places. The left end of the rope exerts an upward force  on the worker’s hands. This force arises because he pulls downward with a 540-N force, and the rope exerts an oppositely directed force of equal magnitude on him, in accord with Newton’s third law. Thus, the magnitude T of the upward force is T = 540 N and is the magnitude of the tension in the rope. If the masses of the rope and each pulley are negligible and if the pulleys are friction-free, the tension is transmitted undiminished along the rope. Then, a 540-N tension force on the worker’s hands. This force arises because he pulls downward with a 540-N force, and the rope exerts an oppositely directed force of equal magnitude on him, in accord with Newton’s third law. Thus, the magnitude T of the upward force is T = 540 N and is the magnitude of the tension in the rope. If the masses of the rope and each pulley are negligible and if the pulleys are friction-free, the tension is transmitted undiminished along the rope. Then, a 540-N tension force  acts upward on the left side of the scaffold pulley (see part a of the drawing). A tension force is also applied to the point P, where the rope attaches to the roof. The roof pulls back on the rope in accord with the third law, and this pull leads to the 540-N tension force acts upward on the left side of the scaffold pulley (see part a of the drawing). A tension force is also applied to the point P, where the rope attaches to the roof. The roof pulls back on the rope in accord with the third law, and this pull leads to the 540-N tension force  that acts on the right side of the scaffold pulley. In addition to the three upward forces, the weight of the unit must be taken into account [ that acts on the right side of the scaffold pulley. In addition to the three upward forces, the weight of the unit must be taken into account [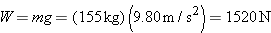 ]. Part b of the drawing shows the free-body diagram. ]. Part b of the drawing shows the free-body diagram.Solution Newton’s second law ( 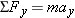 ) can be applied to calculate the acceleration ay: ) can be applied to calculate the acceleration ay:
| |||||||||||||||
 |
 Check Your Understanding 5 Check Your Understanding 5 |
Two boxes have masses m1 and m2, and m2 is greater than m1. The boxes are being pushed across a frictionless horizontal surface. As the drawing shows, there are two possible arrangements, and the pushing force is the same in each. In which arrangement does the force that the left box applies to the right box have a greater magnitude, or is the magnitude the same in both cases? (The answer is given at the end of the book.)
Background: This question deals with net force, acceleration, and Newton’s second and third laws of motion. For similar questions (including calculational counterparts), consult Self-Assessment Test 4.3. The test is described next. |

| ||||||||||
|
Test your understanding of the material in Sections 4.11 and 4.12:
| ||||||||||
| Copyright © 2007 John Wiley & Sons, Inc. All rights reserved. |