4.13 |
Concepts & Calculations |
|
| ||
| ||||||||||||||||||||||||||||||
|
Figure 4-38 shows two forces, 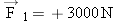 and and 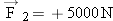 , acting on a spacecraft, where the plus signs indicate that the forces are directed along the +x axis. A third force , acting on a spacecraft, where the plus signs indicate that the forces are directed along the +x axis. A third force 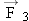 also acts on the spacecraft but is not shown in the drawing. The craft is moving with a constant velocity of +850 m/s. Find the magnitude and direction of also acts on the spacecraft but is not shown in the drawing. The craft is moving with a constant velocity of +850 m/s. Find the magnitude and direction of  . .
Concept Questions and Answers Suppose the spacecraft were stationary. What would be the direction of 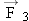 ? ?
When the spacecraft is moving at a constant velocity of +850 m/s, what is the direction of 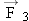 ? ?
Solution Since the velocity is constant, the acceleration is zero. The net force must also be zero, so that
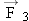 points opposite to the sum of points opposite to the sum of  and and  , or along the −x axis in Figure 4-38. The force , or along the −x axis in Figure 4-38. The force 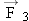 has a magnitude of 8000 N, which is the magnitude of the sum of the forces  and and  . The answer is independent of the velocity of the spacecraft, as long as that velocity remains constant. . The answer is independent of the velocity of the spacecraft, as long as that velocity remains constant. | ||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||
|
On earth a block has a weight of 88 N. This block is sliding on a horizontal surface on the moon, where the acceleration due to gravity is 1.60 m/s2. As Figure 4-39a shows, the block is being pulled by a horizontal rope in which the tension is T = 24 N. The coefficient of kinetic friction between the block and the surface is 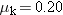 . Determine the acceleration of the block. . Determine the acceleration of the block.
Concept Questions and Answers Which of Newton’s laws of motion provides a way to determine the acceleration of the block?
This problem deals with a situation on the moon, but the block’s mass on the moon is not given. Instead, the block’s earth-weight is given. Why can the earth-weight be used to obtain a value for the block’s mass that applies on the moon?
Does the net force 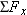 equal the tension T ? equal the tension T ?
Solution Figure 4-39b shows the free-body diagram for the block. The net force along the x axis is 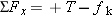 , where T is the magnitude of the tension in the rope and fk is the magnitude of the kinetic frictional force. According to Equation 4.8, fk is related to the magnitude FN of the normal force by , where T is the magnitude of the tension in the rope and fk is the magnitude of the kinetic frictional force. According to Equation 4.8, fk is related to the magnitude FN of the normal force by 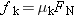 , where , where 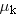 is the coefficient of kinetic friction. The acceleration ax of the block is given by Newton’s second law as is the coefficient of kinetic friction. The acceleration ax of the block is given by Newton’s second law as
 . Therefore, the net force . Therefore, the net force 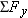 along the y direction must also be zero. An examination of the free-body diagram reveals that along the y direction must also be zero. An examination of the free-body diagram reveals that 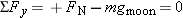 , so that , so that 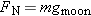 . The acceleration in the x direction becomes . The acceleration in the x direction becomes
| ||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||
| Copyright © 2007 John Wiley & Sons, Inc. All rights reserved. |