| | 4.1 THE CONCEPTS OF FORCE AND MASS | |
Contact and noncontact forces | A force is a push or a pull and is a vector quantity. Contact forces arise from the physical contact between two objects. Noncontact forces are also called action-at-a-distance forces, because they arise without physical contact between two objects. | |
Mass | Mass is a property of matter that determines how difficult it is to accelerate or decelerate an object. Mass is a scalar quantity. | |
| | 4.2 NEWTON’s FIRST LAW OF MOTION | |
Newton’s first law | Newton’s first law of motion, sometimes called the law of inertia, states that an object continues in a state of rest or in a state of motion at a constant speed along a straight line unless compelled to change that state by a net force. | |
Inertia Mass Inertial reference frame | Inertia is the natural tendency of an object to remain at rest or in motion at a constant speed along a straight line. The mass of a body is a quantitative measure of inertia and is measured in an SI unit called the kilogram (kg). An inertial reference frame is one in which Newton’s law of inertia is valid. | |
| | 4.3 NEWTON’s SECOND LAW OF MOTION | |
| | 4.4 THE VECTOR NATURE OF NEWTON’s SECOND LAW OF MOTION | |
| | Newton’s second law of motion states that when a net force 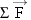 acts on an object of mass m, the acceleration 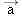 of the object can be obtained from the following equation: | |
Newtons’s second law (vector form) | | |
| | This is a vector equation and, for motion in two dimensions, is equivalent to the following two equations: | |
Newtons’s second law (component form) | | |
| | In these equations the x and y subscripts refer to the scalar components of the force and acceleration vectors. The SI unit of force is the Newton (N). | |
Free-body diagram | When determining the net force, a free-body diagram is helpful. A free-body diagram is a diagram that represents the object and the forces acting on it. | |
| | 4.5 NEWTON’s THIRD LAW OF MOTION | |
Newton’s third law of motion | Newton’s third law of motion, often called the action–reaction law, states that whenever one object exerts a force on a second object, the second object exerts an oppositely directed force of equal magnitude on the first object. | |
 |  Use Self-Assessment Test 4.1 to evaluate your understanding of Sections 4.1, 4.2, 4.3, 4.4 and 4.5. Use Self-Assessment Test 4.1 to evaluate your understanding of Sections 4.1, 4.2, 4.3, 4.4 and 4.5. |  |  |  |
|
| | 4.6 TYPES OF FORCES: AN OVERVIEW | |
Fundmental forces | Only three fundamental forces have been discovered: the gravitational force, the strong nuclear force, and the electroweak force. The electroweak force manifests itself as either the electromagnetic force or the weak nuclear force. | |
| | 4.7 THE GRAVITATIONAL FORCE | |
| | Newton’s law of universal gravitation states that every particle in the universe exerts an attractive force on every other particle. For two particles that are separated by a distance r and have masses m1 and m2, the law states that the magnitude of this attractive force is | |
Newton’s law of universal gravitation | | |
| | The direction of this force lies along the line between the particles. The constant G has a value of 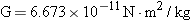 and is called the universal gravitational constant. | |
| | The weight W of an object on or above the earth is the gravitational force that the earth exerts on the object and can be calculated from the mass m of the object and the acceleration g due to the earth’s gravity according to | |
Weight and mass | | |
| | 4.8 THE NORMAL FORCE | |
Normal force | The normal force  is one component of the force that a surface exerts on an object with which it is in contact—namely, the component that is perpendicular to the surface. | |
| | The apparent weight is the force that an object exerts on the platform of a scale and may be larger or smaller than the true weight mg if the object and the scale have an acceleration a (+ if upward, − if downward). The apparent weight is | |
Apparent weight | | |
| | 4.9 STATIC AND KINETIC FRICTIONAL FORCES | |
Friction | A surface exerts a force on an object with which it is in contact. The component of the force perpendicular to the surface is called the normal force. The component parallel to the surface is called friction. | |
| | The force of static friction between two surfaces opposes any impending relative motion of the surfaces. The magnitude of the static frictional force depends on the magnitude of the applied force and can assume any value up to a maximum of | |
Maximum static frictional force | | |
| | where 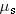 is the coefficient of static friction and FN is the magnitude of the normal force. | |
| | The force of kinetic friction between two surfaces sliding against one another opposes the relative motion of the surfaces. This force has a magnitude given by | |
Kinetic frictional force | | |
| | where 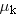 is the coefficient of kinetic friction. | |
| | 4.10 THE TENSION FORCE | |
| | The word “tension” is commonly used to mean the tendency of a rope to be pulled apart due to forces that are applied at each end. Because of tension, a rope transmits a force from one end to the other. When a rope is accelerating, the force is transmitted undiminished only if the rope is massless. | |
 |  Use Self-Assessment Test 4.2 to evaluate your understanding of Sections 4.6, 4.7, 4.8, 4.9 and 4.10. Use Self-Assessment Test 4.2 to evaluate your understanding of Sections 4.6, 4.7, 4.8, 4.9 and 4.10. |  |  |  |
|
| | 4.11 EQUILIBRIUM APPLICATIONS OF NEWTON’s LAWS OF MOTION | |
Definition of equilibrium | An object is in equilibrium when the object has zero acceleration, or, in other words, when it moves at a constant velocity (which may be zero). The sum of the forces that act on an object in equilibrium is zero. Under equilibrium conditions in two dimensions, the separate sums of the force components in the x direction and in the y direction must each be zero: | |
The equilibrium condition | | |
| | 4.12 NONEQUILIBRIUM APPLICATIONS OF NEWTON’s LAWS OF MOTION | |
| | If an object is not in equilibrium, then Newton’s second law must be used to account for the acceleration: | |
| | | |
 |  Use Self-Assessment Test 4.3 to evaluate your understanding of Sections 4.11 and 4.12. Use Self-Assessment Test 4.3 to evaluate your understanding of Sections 4.11 and 4.12. |  |  |  |
|