4.4 |
The Vector Nature of Newton’s Second Law of Motion |
|
| ||
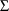 [&~bf~Fˆ{*N*[−6.5%0.0]|bfArarr|}&] in Newton’s second law has components
[&~bf~Fˆ{*N*[−6.5%0.0]|bfArarr|}&] in Newton’s second law has components 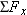 and
and 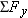 , while the acceleration
, while the acceleration  has components ax and ay. Consequently, Newton’s second law, as expressed in Equation 4.1, can be written in an equivalent form as two equations, one for the x components and one for the y components:
has components ax and ay. Consequently, Newton’s second law, as expressed in Equation 4.1, can be written in an equivalent form as two equations, one for the x components and one for the y components:
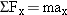
| (4.2a) |
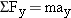
| (4.2b) |
| ||||||||||||||||||||||||||||||||||||
|
A man is stranded on a raft (mass of man and raft = 1300 kg), as shown in Figure 4-6a. By paddling, he causes an average force 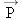 of 17 N to be applied to the raft in a direction due east (the +x direction). The wind also exerts a force of 17 N to be applied to the raft in a direction due east (the +x direction). The wind also exerts a force 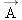 on the raft. This force has a magnitude of 15 N and points 67° north of east. Ignoring any resistance from the water, find the x and y components of the raft’s acceleration. on the raft. This force has a magnitude of 15 N and points 67° north of east. Ignoring any resistance from the water, find the x and y components of the raft’s acceleration.Reasoning Since the mass of the man and the raft is known, Newton’s second law can be used to determine the acceleration components from the given forces. According to the form of the second law in Equations 4.2a and 4.2b, the acceleration component in a given direction is the component of the net force in that direction divided by the mass. As an aid in determining the components 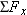 and and 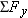 of the net force, we use the free-body diagram in Figure 4-6b. In this diagram, the directions due east and due north are the +x and +y directions, respectively. of the net force, we use the free-body diagram in Figure 4-6b. In this diagram, the directions due east and due north are the +x and +y directions, respectively.
Solution Figure 4-6b shows the force components:
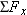 points in the direction of the +x axis and points in the direction of the +x axis and 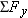 points in the direction of the +y axis. The x and y components of the acceleration point in the directions of points in the direction of the +y axis. The x and y components of the acceleration point in the directions of 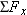 and and 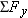 , respectively, and can now be calculated: , respectively, and can now be calculated:
| ||||||||||||||||||||||||||||||||||||
 |
| ||||||
|
At the moment the forces 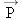 and and 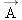 begin acting on the raft in Example 2, the velocity of the raft is 0.15 m/s, in a direction due east (the +x direction). Assuming that the forces are maintained for 65 s, find the x and y components of the raft’s displacement during this time interval. begin acting on the raft in Example 2, the velocity of the raft is 0.15 m/s, in a direction due east (the +x direction). Assuming that the forces are maintained for 65 s, find the x and y components of the raft’s displacement during this time interval.Reasoning Once the net force acting on an object and the object’s mass have been used in Newton’s second law to determine the acceleration, it becomes possible to use the equations of kinematics to describe the resulting motion. We know from Example 2 that the acceleration components are 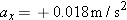 and and 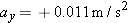 , and it is given here that the initial velocity components are , and it is given here that the initial velocity components are 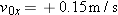 and and 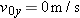 . Thus, Equation 3.5a . Thus, Equation 3.5a 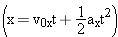 and Equation 3.5b and Equation 3.5b 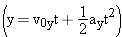 can be used with t = 65 s to determine the x and y components of the raft’s displacement. can be used with t = 65 s to determine the x and y components of the raft’s displacement.Solution According to Equations 3.5a and 3.5b, the x and y components of the displacement are
| ||||||
 |
Problem solving insight Applications of Newton’s second law always involve the net external force, which is the vector sum of all the external forces that act on an object. Each component of the net force leads to a corresponding component of the acceleration. |
 Check Your Understanding 1 Check Your Understanding 1 |
All of the following, except one, cause the acceleration of an object to double. Which one is it? (a) All forces acting on the object double. (b) The net force acting on the object doubles. (c) Both the net force acting on the object and the mass of the object double. (d) The mass of the object is reduced by a factor of two. (The answer is given at the end of the book.) Background: This problem depends on the concepts of force, net force, mass, and acceleration, because Newton’s second law of motion deals with them. For similar questions (including calculational counterparts), consult Self-Assessment Test 4.1. This test is described at the end of Section 4.5. |
Need more practice?
 |
|
| Copyright © 2007 John Wiley & Sons, Inc. All rights reserved. |