Applying Newton's Second Law Using Components

Example 2 Applying Newton's Second Law Using Components

A man is stranded on a raft (mass of man and raft = 1300 kg), as shown in Figure 4.6a. By paddling, he causes an average force

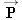
of 17 N to be applied to the raft in a direction due east (the +x direction). The wind also exerts a force

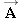
on the raft. This force has a magnitude of 15 N and points 67° north of east. Ignoring any resistance from the water, find the x and y components of the raft's acceleration.

Figure 4.6

(a)

A man is paddling a raft, as in Examples 2 and 3.

(b)

The free-body diagram shows the forces 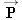and 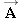that act on the raft. Forces acting on the raft in a direction perpendicular to the surface of the water play no role in the examples and are omitted for clarity.

(c)

The raft's acceleration components a_x and a_y.

(d)

In 65 s, the components of the raft's displacement are x = 48 m and y = 23 m.

Problem-solving insight

Applications of Newton's second law always involve the net external force, which is the vector sum of all the external forces that act on an object. Each component of the net force leads to a corresponding component of the acceleration.

Reasoning Since the mass of the man and the raft is known, Newton's second law can be used to determine the acceleration components from the given forces. According to the form of the second law in Equations 4.2a and 4.2b, the acceleration component in a given direction is the component of the net force in that direction divided by the mass. As an aid in determining the components ΣF_x and ΣF_y of the net force, we use the free-body diagram in Figure 4.6b. In this diagram, the directions due east and due north are the +x and +y directions, respectively.

Solution Figure 4.6b shows the force components:

Force	x Component	y Component
	+17 N	0 N
	+(15 N) cos 67° = +6 N	+(15 N) sin 67° = +14 N

The plus signs indicate that ΣF_x points in the direction of the +x axis and ΣF_y points in the direction of the +y axis. The x and y components of the acceleration point in the directions of ΣF_x and ΣF_y, respectively, and can now be calculated:


	(4.2a)


	(4.2b)

These acceleration components are shown in Figure 4.6c.