Equilibrium at Constant Velocity

Example 13 Equilibrium at Constant Velocity

A jet plane is flying with a constant speed along a straight line, at an angle of 30.0° above the horizontal, as Figure 4.30a indicates. The plane has a weight

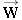
whose magnitude is W = 86 500 N, and its engines provide a forward thrust

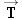
of magnitude T = 103 000 N. In addition, the lift force

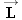
(directed perpendicular to the wings) and the force

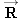
of air resistance (directed opposite to the motion) act on the plane. Find

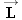
and

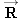
Figure 4.30

(a)

A plane moves with a constant velocity at an angle of 30.0° above the horizontal due to the action of four forces, the weight 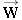, the lift 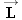, the engine thrust 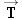, and the air resistance .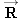

(b)

The free-body diagram for the plane.

(c)

This geometry occurs often in physics.

Problem-solving insight

A moving object is in equilibrium if it moves with a constant velocity; then its acceleration is zero. A zero acceleration is the fundamental characteristic of an object in equilibrium.

Reasoning Figure 4.30b shows the free-body diagram of the plane, including the forces

, and

. Since the plane is not accelerating, it is in equilibrium, and the sum of the x components and the sum of the y components of these forces must be zero. The lift force

and the force

of air resistance can be obtained from these equilibrium conditions. To calculate the components, we have chosen axes in the free-body diagram that are rotated by 30.0° from their usual horizontal–vertical positions. This has been done purely for convenience, since the weight

is then the only force that does not lie along either axis.

Solution When determining the components of the weight, it is necessary to realize that the angle β in Figure 4.30a is 30.0°. Part c of the drawing focuses attention on the geometry that is responsible for this fact. There it can be seen that α + β = 90° and α + 30.0° = 90°, with the result that β = 30.0°. The table below lists the components of the forces that act on the jet.

Force	x Component	y Component
	-W sin 30.0°	-W cos 30.0°
	0	+L
	+T	0
	-R	0

Setting the sum of the x component of the forces to zero gives


	(4.9a)

Setting the sum of the y component of the forces to zero gives


	(4.9b)