A supertanker of mass
m = 1.50 × 10
8 kg is being towed by two tugboats, as in Figure 4.31
a. The tensions in the towing cables apply the forces

and

at equal angles of 30.0° with respect to the tanker's axis. In addition, the tanker's engines produce a forward drive force
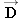
, whose magnitude is
D = 75.0 × 10
3 N. Moreover, the water applies an opposing force
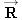
, whose magnitude is
R = 40.0 × 10
3 N. The tanker moves forward with an acceleration that points along the tanker's axis and has a magnitude of 2.00 × 10
-3 m/s
2. Find the magnitudes of the tensions

and

.
 |
 |
|
|
 |
| Figure 4.31 |
 |
|
(a)
|
Four forces act on a supertanker:  and  are the tension forces due to the towing cables, 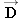 is the forward drive force produced by the tanker's engines, and 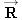 is the force with which the water opposes the tanker's motion.
|
 |
|
(b)
|
The free-body diagram for the tanker.
|
|
|
|
 |
|
 |
Solution
The individual force components are summarized as follows:
 |
 |
|
Force
|
x Component
|
y Component
|
|
|
+T1 cos 30.0°
|
+T1 sin 30.0°
|
|
|
+T2 cos 30.0°
|
-T2 sin 30.0°
|
|
|
+D
|
0
|
|
|
-R
|
0
|
|
|
|
|
 |
|
 |
Since the acceleration points along the
x axis, there is no
y component of the acceleration (
ay = 0 m/s
2). Consequently, the sum of the
y components of the forces must be zero:
This result shows that the magnitudes of the tensions in the cables are equal,
T1 =
T2. Since the ship accelerates along the
x direction, the sum of the
x components of the forces is not zero. The second law indicates that
Since
T1 =
T2, we can replace the two separate tension symbols by a single symbol
T, the magnitude of the tension. Solving for
T gives



