 |
 |
 |
|
A window washer on a scaffold is hoisting the scaffold up the side of a building by pulling downward on a rope, as in Figure
4.36 a. The magnitude of the pulling force is 540 N, and the combined mass of the worker and the scaffold is 155 kg. Find the upward
acceleration of the unit.
 |
 |
|
|
 |
| Figure 4.36 |
 |
|
(a)
|
A window washer pulls down on the rope to hoist the scaffold up the side of a building. The force 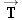 results from the effort of the window washer and acts on him and the scaffold in three places, as discussed in Example 19.
|
 |
|
(b)
|
The free-body diagram of the unit comprising the man and the scaffold.
|
|
|
|
 |
|
 |
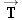 on the worker's hands. This force arises because he pulls downward with a 540-N force, and the rope exerts an oppositely
directed force of equal magnitude on him, in accord with Newton's third law. Thus, the magnitude T of the upward force is T = 540 N and is the magnitude of the tension in the rope. If the masses of the rope and each pulley are negligible and if
the pulleys are friction-free, the tension is transmitted undiminished along the rope. Then, a 540-N tension force on the worker's hands. This force arises because he pulls downward with a 540-N force, and the rope exerts an oppositely
directed force of equal magnitude on him, in accord with Newton's third law. Thus, the magnitude T of the upward force is T = 540 N and is the magnitude of the tension in the rope. If the masses of the rope and each pulley are negligible and if
the pulleys are friction-free, the tension is transmitted undiminished along the rope. Then, a 540-N tension force 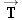 acts upward on the left side of the scaffold pulley (see part a of the drawing). A tension force is also applied to the point P, where the rope attaches to the roof. The roof pulls back on the rope in accord with the third law, and this pull leads to
the 540-N tension force acts upward on the left side of the scaffold pulley (see part a of the drawing). A tension force is also applied to the point P, where the rope attaches to the roof. The roof pulls back on the rope in accord with the third law, and this pull leads to
the 540-N tension force 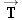 that acts on the right side of the scaffold pulley. In addition to the three upward forces, the weight of the unit must be
taken into account [W = mg = (155 kg)(9.80 m/s2) = 1520 N]. Part b of the drawing shows the free-body diagram. that acts on the right side of the scaffold pulley. In addition to the three upward forces, the weight of the unit must be
taken into account [W = mg = (155 kg)(9.80 m/s2) = 1520 N]. Part b of the drawing shows the free-body diagram.
Solution
Newton's second law (Σ Fy = may) can be applied to calculate the acceleration ay:
|
 |
 |
|
 |
 |
|
 |



