Figure 4.37 shows two forces,
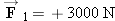
and
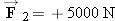
, acting on a spacecraft; the plus signs indicate that the forces are directed along the +
x axis. A third force
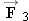
also acts on the spacecraft but is not shown in the drawing. The craft is moving with a constant velocity of +850 m/s. Find
the magnitude and direction of
.
 |
 |
|
|
 |
| Figure 4.37 |
Two horizontal forces, 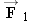 and and 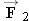 , act on the spacecraft. A third force , act on the spacecraft. A third force 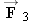 also acts but is not shown. also acts but is not shown.
|
|
 |
|
 |
|
Concept Questions and Answers |
 |
|
Suppose the spacecraft were stationary. What would be the direction of 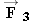 ?
Answer:
If the spacecraft were stationary, its acceleration would be zero. According to Newton's second law, the acceleration of an
object is proportional to the net force acting on it. Thus, the net force must also be zero. But the net force is the vector
sum of the three forces in this case. Therefore, the force 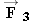 must have a direction such that it balances to zero the forces 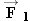 and 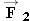 . Since 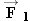 and 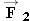 point along the + x axis in Figure 4.37, 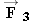 must then point along the - x axis.
|
 |
 |
|
When the spacecraft is moving at a constant velocity of +850 m/s, what is the direction of 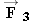 ?
Answer:
Since the velocity is constant, the acceleration is still zero. As a result, everything we said in the stationary case applies
again here. The net force is zero, and the force 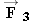 must point along the - x axis in Figure 4.37.
|
 |
 |
|
Solution
Since the velocity is constant, the acceleration is zero. The net force must also be zero, so that
Solving for
F3 yields
The minus sign in the answer means that
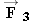
points opposite to the sum of
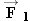
and
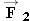
, or along the -
x axis in Figure 4.37. The force
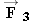
has a magnitude of 8000 N, which is the magnitude of the sum of the forces
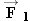
and
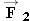
. The answer is independent of the velocity of the spacecraft, as long as that velocity remains constant.



