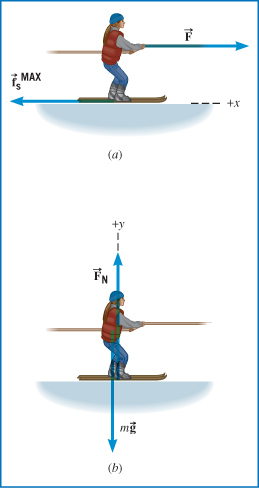
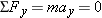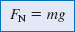A skier is standing motionless on a horizontal patch of snow. She is holding onto a horizontal tow rope, which is about to
pull her forward (see Figure 4.22a). The skier's mass is 59 kg, and the coefficient of static friction between the skis and snow is 0.14. What is the magnitude
of the maximum force that the tow rope can apply to the skier without causing her to move?
Reasoning
When the rope applies a relatively small force, the skier does not accelerate. The reason is that the static frictional force
opposes the applied force and the two forces have the same magnitude. We can apply Newton's second law in the horizontal direction
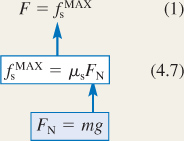
to this situation. In order for the rope to pull the skier forward, it must exert a force large enough to overcome the maximum static frictional force acting on the skis. The magnitude of the maximum static frictional force depends on the coefficient
of static friction (which is known) and on the magnitude of the normal force. We can determine the magnitude of the normal
force by using Newton's second law, along with the fact that the skier does not accelerate in the vertical direction.
|
|||||||||||||||||||||
Knowns and Unknowns The data for this problem are as follows:
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Solution
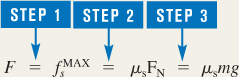
Algebraically combining the results of the three steps, we have
The magnitude F of the maximum force is
If the force exerted by the tow rope exceeds this value, the skier will begin to accelerate forward.
|
||||||
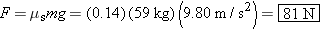 |
|

 applied by the tow rope and the maximum static frictional force
applied by the tow rope and the maximum static frictional force 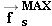 . Since the skier is standing motionless, she is not accelerating in the horizontal or
. Since the skier is standing motionless, she is not accelerating in the horizontal or 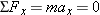
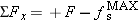 , Newton's second law can be written as
, Newton's second law can be written as 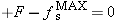 . Thus,
. Thus,
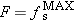
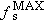 , but its value will be determined in Steps 2 and 3.
, but its value will be determined in Steps 2 and 3.
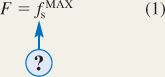

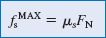

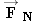 and her weight
and her weight 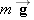 . Applying Newton's second law (Equation 4.2b) to the vertical direction gives
. Applying Newton's second law (Equation 4.2b) to the vertical direction gives