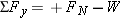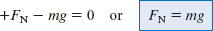|
A sled and its rider are moving at a speed of 4.0 m/s along a horizontal stretch of snow, as Figure 4.24 a illustrates. The snow exerts a kinetic frictional force on the runners of the sled, so the sled slows down and eventually
comes to a stop. The coefficient of kinetic friction is 0.050. What is the displacement x of the sled?
 |
 |
|
|
 |
| Figure 4.24 |
 |
|
(a)
|
The moving sled decelerates because of the kinetic frictional force.
|
 |
|
(b)
|
Three forces act on the moving sled, the weight  of the sled and its rider, the normal force 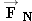 , and the kinetic frictional force 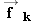 . The free-body diagram for the sled shows these forces.
|
|
|
|
 |
|
 |
Knowns and Unknowns
The data for this problem are listed in the table:
 |
 |
|
Description
|
Symbol
|
Value
|
Comment
|
|
Explicit Data
|
|
|
|
|
Initial velocity
|
v0x
|
+4.0 m/s
|
Positive, because the velocity points in the +x direction. See drawing.
|
|
Coefficient of kinetic friction
|
μk
|
0.050
|
|
|
Implicit Data
|
|
|
|
|
Final velocity
|
vx
|
0 m/s
|
The sled comes to a stop.
|
|
Unknown Variable
|
|
|
|
|
Displacement
|
x
|
?
|
|
|
|
|
|
 |
|
 |
 |
 |
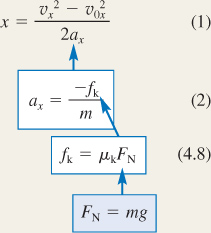
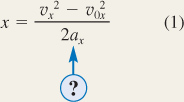
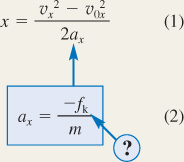
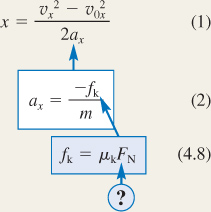
 Displacement Displacement To obtain the displacement x of the sled we will use Equation 3.6a from the equations of kinematics:
Solving for the displacement x gives the result shown at the right. This equation is useful because two of the variables, v0x and vx, are known and the acceleration ax can be found by applying Newton's second law to the accelerating sled (see Step 2).
|
|
 Newton's Second Law Newton's Second Law Newton's second law, as given in Equation 4.2a, states that the acceleration ax is equal to the net force Σ Fx divided by the mass m:
The free-body diagram in Figure 4.24 b shows that the only force acting on the sled in the horizontal or x direction is the kinetic frictional force 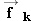 . We can write this force as - fk, where fk is the magnitude of the force and the minus sign indicates that it points in the - x direction. Since the net force is Σ Fx = - fk, Equation 4.2a becomes
This result can now be substituted into Equation 1, as shown at the right.
|
|
 Kinetic Frictional Force Kinetic Frictional Force We do not know the magnitude fk of the kinetic frictional force, but we do know the coefficient of kinetic friction μ k. According to Equation 4.8, the two are related by
where FN is the magnitude of the normal force. This relation can be substituted into Equation 2, as shown at the right. An expression
for FN will be obtained in the next step.
|
|
 Normal Force Normal Force The magnitude FN of the normal force can be found by noting that the sled does not accelerate in the vertical or y direction ( ay = 0 m/s 2). Thus, Newton's second law, as given in Equation 4.2b becomes
There are two forces acting on the sled in the y direction, the normal force 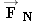 and its weight 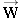 [see part (b) of the drawing]. Therefore, the net force in the y direction is
where W = mg (Equation 4.5). Thus, Newton's second law becomes
This result for FN can be substituted into Equation 4.8, as shown at the right.
|
|
|
|
|
|
 |
|
 |
Solution
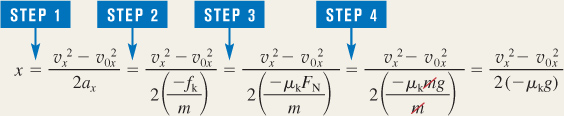
Algebraically combining the results of each step, we find that
Note that the mass m of the sled and rider is algebraically eliminated from the final result. Thus, the displacement of the sled is
|
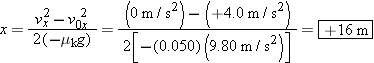
 of the sled and its rider, the normal force
of the sled and its rider, the normal force 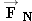 , and the kinetic frictional force
, and the kinetic frictional force 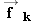 . The free-body diagram for the sled shows these forces.
. The free-body diagram for the sled shows these forces.

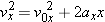

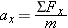
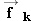 . We can write this force as -
. We can write this force as -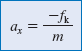

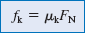

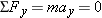
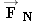 and its weight
and its weight 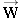 [see part (b) of the drawing]. Therefore, the net force in the
[see part (b) of the drawing]. Therefore, the net force in the