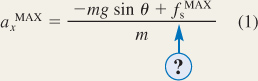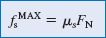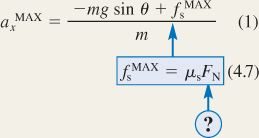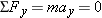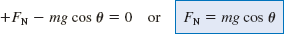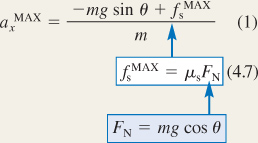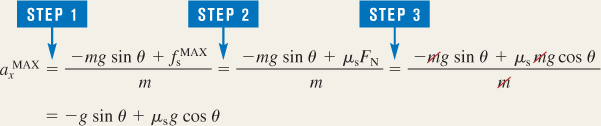A flatbed truck is carrying a crate up a 10.0° hill, as Figure 4.34a illustrates. The coefficient of static friction between the truck bed and the crate is 0.350. Find the maximum acceleration
that the truck can attain before the crate begins to slip backward relative to the truck.
Reasoning
The crate will not slip as long as it has the same acceleration as the truck. Therefore, a net force must act on the crate
to accelerate it, and the static frictional force
|
|||||||||||||||||||||
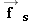 contributes to this net force. Since the crate tends to slip backward, the static frictional force is directed forward, up
the hill.
contributes to this net force. Since the crate tends to slip backward, the static frictional force is directed forward, up
the hill.As the acceleration of the truck increases,
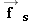 must also increase to produce a corresponding increase in the acceleration of the crate. However, the static frictional force
can increase only until its maximum value
must also increase to produce a corresponding increase in the acceleration of the crate. However, the static frictional force
can increase only until its maximum value 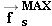 is reached, at which point the crate and truck have the maximum acceleration
is reached, at which point the crate and truck have the maximum acceleration 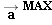 . If the acceleration increases even more, the crate will slip.
. If the acceleration increases even more, the crate will slip.To find
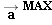 , we will employ Newton's second law, the definition of weight, and the relationship between the maximum static frictional
force and the normal force.
, we will employ Newton's second law, the definition of weight, and the relationship between the maximum static frictional
force and the normal force.Knowns and Unknowns The data for this problem are as follows:
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Solution
Algebraically combining the results of the three steps, we find that
Note that the mass m of the crate is algebraically eliminated from the final result. Thus, the maximum acceleration is
|
||||||
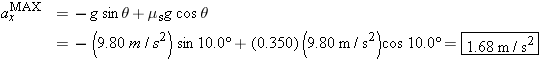 |
|
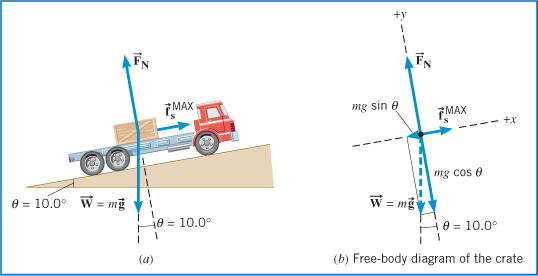
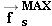 . The other forces that act on the crate are its weight
. The other forces that act on the crate are its weight  and the normal force
and the normal force 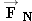 .
.

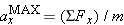 , where Σ
, where Σ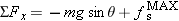 . Substituting this expression into Newton's second law gives
. Substituting this expression into Newton's second law gives
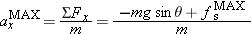
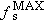 are not. We will now turn our attention to finding
are not. We will now turn our attention to finding