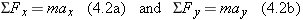Nonequilibrium Applications of Newton's Laws of Motion
When an object is accelerating, it is not in equilibrium, as indicated in Figure 4.27. The forces acting on it are not balanced, so the net force is not zero in Newton's second law. However, with one exception, the reasoning strategy followed in solving nonequilibrium problems is identical to that used in equilibrium situations. The exception occurs in Step 4 of the five steps outlined at the beginning of the last section. Since the object is now accelerating, the representation of Newton's second law in Equations 4.2a and 4.2b applies instead of Equations 4.9a and 4.9b:
Example 14 uses these equations in a situation where the forces are applied in directions similar to those in Example 11, except that now an acceleration is present.
Example  14  Towing a Supertanker
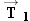
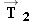
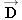
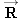
A supertanker of mass m = 1.50 × 108 kg is being towed by two tugboats, as in Figure 4.31a. The tensions in the towing cables apply the forces and at equal angles of 30.0° with respect to the tanker's axis. In addition, the tanker's engines produce a forward drive force , whose magnitude is D = 75.0 × 103 N. Moreover, the water applies an opposing force , whose magnitude is R = 40.0 × 103 N. The tanker moves forward with an acceleration that points along the tanker's axis and has a magnitude of 2.00 × 10-3 m/s2. 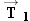Find the magnitudes of the tensions and .
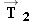
Figure 4.31   

(a)  
Four forces act on a supertanker: and 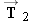are the tension forces due to the towing cables, 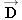is the forward drive force produced by the tanker's engines, and 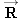is the force with which the water opposes the tanker's motion.
(b)  
The free-body diagram for the tanker.


Reasoning   The unknown forces and contribute to the net force that accelerates the tanker. To determine and , therefore, we analyze the net force, which we will do using components. The various force components can be found by referring to the free-body diagram for the tanker in Figure 4.31b, where the ship's axis is chosen as the x axis. We will then use Newton's second law in its component form, ΣFx = max and ΣFy = may, to obtain the magnitudes of and .

Solution   The individual force components are summarized as follows:
Force
x Component
y Component
+T1 cos 30.0°
+T1 sin 30.0°
+T2 cos 30.0°
-T2 sin 30.0°
+D
0
-R
0
Since the acceleration points along the x axis, there is no y component of the acceleration (ay = 0 m/s2). Consequently, the sum of the y components of the forces must be zero:
This result shows that the magnitudes of the tensions in the cables are equal, T1 = T2. Since the ship accelerates along the x direction, the sum of the x components of the forces is not zero. The second law indicates that
Since T1 = T2, we can replace the two separate tension symbols by a single symbol T, the magnitude of the tension. Solving for T gives


It often happens that two objects are connected somehow, perhaps by a drawbar like that used when a truck pulls a trailer. If the tension in the connecting device is of no interest, the objects can be treated as a single composite object when applying Newton's second law. However, if it is necessary to find the tension, as in the next example, then the second law must be applied separately to at least one of the objects.
Example  15  Hauling a Trailer
A truck is hauling a trailer along a level road, as Figure 4.32a illustrates. The mass of the truck is m1 = 8500 kg and that of the trailer is m2 = 27 000 kg. The two move along the x axis with an acceleration of ax = 0.78 m/s2. Ignoring the retarding forces of friction and air resistance, determine (a) the tension in the horizontal drawbar between the trailer and the truck and (b) the force that propels the truck forward.
Figure 4.32   

(a)  
The force acts on the truck and propels it forward. The drawbar exerts the tension force on the truck and the tension force on the trailer.
(b)  
The free-body diagrams for the trailer and the truck, ignoring the vertical forces.


Reasoning   Since the truck and the trailer accelerate along the horizontal direction and friction is being ignored, only forces that have components in the horizontal direction are of interest. Therefore, Figure 4.32 omits the weight and the normal force, which act vertically. To determine the tension force in the drawbar, we draw the free-body diagram for the trailer and apply Newton's second law, ΣFx = max. Similarly, we can determine the propulsion force by drawing the free-body diagram for the truck and applying Newton's second law.

Solution  

(a)  
The free-body diagram for the trailer is shown in Figure 4.32b. There is only one horizontal force acting on the trailer, the tension force due to the drawbar. Therefore, it is straightforward to obtain the tension from ΣFx = m2ax, since the mass of the trailer and the acceleration are known:
(b)  
Two horizontal forces act on the truck, as the free-body diagram in Figure 4.32b shows. One is the desired force . The other is the force . According to Newton's third law, is the force with which the trailer pulls back on the truck, in reaction to the truck pulling forward. If the drawbar has negligible mass, the magnitude of is equal to the magnitude of —namely, 21 000 N. Since the magnitude of , the mass of the truck, and the acceleration are known, ΣFx = m1ax can be used to determine the drive force:


In Section 4.11 we examined situations where the net force acting on an object is zero, and in this section we have considered two examples where the net force is not zero. Conceptual Example 16 illustrates a common situation where the net force is zero at certain times but is not zero at other times.
  Conceptual Example 16  The Motion of a Water Skier
Figure 4.33 shows a water skier at four different moments:

(a)  
The skier is floating motionless in the water.
(b)  
The skier is being pulled out of the water and up onto the skis.
(c)  
The skier is moving at a constant speed along a straight line.
(d)  
The skier has let go of the tow rope and is slowing down.

For each moment, explain whether the net force acting on the skier is zero.
Figure 4.33    A water skier (a) floating in water, (b) being pulled up by the boat, (c) moving at a constant velocity, and (d) slowing down.

Reasoning and Solution   According to Newton's second law, if an object has zero acceleration, the net force acting on it is zero. In such a case, the object is in equilibrium. In contrast, if the object has an acceleration, the net force acting on it is not zero. Such an object is not in equilibrium. We will consider the acceleration in each of the four phases of the motion to decide whether the net force is zero.

(a)  
The skier is floating motionless in the water, so her velocity and acceleration are both zero. Therefore, the net force acting on her is zero, and she is in equilibrium.
(b)  
As the skier is being pulled up and out of the water, her velocity is increasing. Thus, she is accelerating, and the net force acting on her is not zero. The skier is not in equilibrium. The direction of the net force is shown in Figure 4.33b.
(c)  
The skier is now moving at a constant speed along a straight line (Figure 4.33c), so her velocity is constant. Since her velocity is constant, her acceleration is zero. Thus, the net force acting on her is zero, and she is again in equilibrium, even though she is moving.
(d)  
After the skier lets go of the tow rope, her speed decreases, so she is decelerating. Thus, the net force acting on her is not zero, and she is not in equilibrium. The direction of the net force is shown in Figure 4.33d.


Related Homework: Problem 78

The force of gravity is often present among the forces that affect the acceleration of an object. Examples 17–19 deal with typical situations.
Analyzing Multiple-Concept Problems

Example   17   Hauling a Crate

A flatbed truck is carrying a crate up a 10.0° hill, as Figure 4.34a illustrates. The coefficient of static friction between the truck bed and the crate is 0.350. Find the maximum acceleration that the truck can attain before the crate begins to slip backward relative to the truck.
Figure 4.34   

(a)  
A crate on a truck is kept from slipping by the static frictional force . The other forces that act on the crate are its weight and the normal force .
(b)  
The free-body diagram of the crate.


Reasoning   The crate will not slip as long as it has the same acceleration as the truck. Therefore, a net force must act on the crate to accelerate it, and the static frictional force contributes to this net force. Since the crate tends to slip backward, the static frictional force is directed forward, up the hill.
As the acceleration of the truck increases, must also increase to produce a corresponding increase in the acceleration of the crate. However, the static frictional force can increase only until its maximum value is reached, at which point the crate and truck have the maximum acceleration . If the acceleration increases even more, the crate will slip.
To find , we will employ Newton's second law, the definition of weight, and the relationship between the maximum static frictional force and the normal force.
Knowns and Unknowns   The data for this problem are as follows:
Description
Symbol
Value
Angle of hill
θ
10.0°
Coefficient of static friction
μs
0.350
Unknown Variable
    
Maximum acceleration before crate slips
aMAX
?

Modeling the Problem
Newton's Second Law (x direction) With the x direction chosen to be parallel to the acceleration of the truck, Newton's second law for this direction can be written as (see Equation 4.2a) , where ΣFx is the net force acting on the crate in the x direction and m is the crate's mass. Using the x components of the forces shown in Figure 4.34b, we find that the net force is . Substituting this expression into Newton's second law gives
The acceleration due to gravity g and the angle θ are known, but m and are not. We will now turn our attention to finding .
The Maximum Static Frictional Force The magnitude of the maximum static frictional force is related to the coefficient of static friction μs and the magnitude FN of the normal force by Equation 4.7:

  (4.7)
This result can be substituted into Equation 1, as shown at the right. Although μs is known, FN is not known. An expression for FN will be found in Step 3, however.
Newton's Second Law (y direction) We can determine the magnitude FN of the normal force by noting that the crate does not accelerate in the y direction (ay = 0 m/s2). Thus, Newton's second law as given in Equation 4.2b becomes
There are two forces acting on the crate in the y direction (see Figure 4.34b): the normal force +FN and the y component of the weight -mg cos θ (The minus sign is included because this component points along the negative y direction.) Thus, the net force is ΣFy = +FN - mg cos θ. Newton's second law becomes
This result for FN can be substituted into Equation 4.7, as indicated at the right.

Solution   Algebraically combining the results of the three steps, we find that
Note that the mass m of the crate is algebraically eliminated from the final result. Thus, the maximum acceleration is

Related Homework: Problems 50, 81, 86
Example  18  Accelerating Blocks
Block 1 (mass m1 = 8.00 kg) is moving on a frictionless 30.0° incline. This block is connected to block 2 (mass m2 = 22.0 kg) by a massless cord that passes over a massless and frictionless pulley (see Figure 4.35a). Find the acceleration of each block and the tension in the cord.
Figure 4.35   

(a)  
Three forces act on block 1: its weight , the normal force , and the force due to the tension in the cord. Two forces act on block 2: its weight and the force due to the tension. The acceleration is labeled according to its magnitude a.
(b)  
Free-body diagrams for the two blocks.


Reasoning   Since both blocks accelerate, there must be a net force acting on each one. The key to this problem is to realize that Newton's second law can be used separately for each block to relate the net force and the acceleration. Note also that both blocks have accelerations of the same magnitude a, since they move as a unit. We assume that block 1 accelerates up the incline and choose this direction to be the +x axis. If block 1 in reality accelerates down the incline, then the value obtained for the acceleration will be a negative number.

Solution   Three forces act on block 1: (1) is its weight [W1 = m1g = (8.00 kg) × (9.80 m/s2) = 78.4 N], (2) is the force applied because of the tension in the cord, and (3) is the normal force that the incline exerts. Figure 4.35b shows the free-body diagram for block 1. The weight is the only force that does not point along the x, y axes, and its x and y components are given in the diagram. Applying Newton's second law (ΣFx = m1ax) to block 1 shows that
where we have set ax = a. This equation cannot be solved as it stands, since both T and a are unknown quantities. To complete the solution, we next consider block 2.

Two forces act on block 2, as the free-body diagram in Figure 4.35b indicates: (1) is its weight [W2 = m2g = (22.0 kg)(9.80 m/s2) = 216 N] and (2) is exerted as a result of block 1 pulling back on the connecting cord. Since the cord and the frictionless pulley are massless, the magnitudes of and are the same: T′ = T. Applying Newton's second law (ΣFy = m2ay) to block 2 reveals that
The acceleration ay has been set equal to -a since block 2 moves downward along the -y axis in the free-body diagram, consistent with the assumption that block 1 moves up the incline. Now there are two equations in two unknowns, and they may be solved simultaneously (see Appendix C) to give T and a:

Example  19  Hoisting a Scaffold
A window washer on a scaffold is hoisting the scaffold up the side of a building by pulling downward on a rope, as in Figure 4.36a. The magnitude of the pulling force is 540 N, and the combined mass of the worker and the scaffold is 155 kg. Find the upward acceleration of the unit.
Figure 4.36   

(a)  
A window washer pulls down on the rope to hoist the scaffold up the side of a building. The force results from the effort of the window washer and acts on him and the scaffold in three places, as discussed in Example 19.
(b)  
The free-body diagram of the unit comprising the man and the scaffold.


Reasoning   The worker and the scaffold form a single unit, on which the rope exerts a force in three places. The left end of the rope exerts an upward force on the worker's hands. This force arises because he pulls downward with a 540-N force, and the rope exerts an oppositely directed force of equal magnitude on him, in accord with Newton's third law. Thus, the magnitude T of the upward force is T = 540 N and is the magnitude of the tension in the rope. If the masses of the rope and each pulley are negligible and if the pulleys are friction-free, the tension is transmitted undiminished along the rope. Then, a 540-N tension force acts upward on the left side of the scaffold pulley (see part a of the drawing). A tension force is also applied to the point P, where the rope attaches to the roof. The roof pulls back on the rope in accord with the third law, and this pull leads to the 540-N tension force that acts on the right side of the scaffold pulley. In addition to the three upward forces, the weight of the unit must be taken into account [W = mg = (155 kg)(9.80 m/s2) = 1520 N]. Part b of the drawing shows the free-body diagram.

Solution   Newton's second law (ΣFy = may) can be applied to calculate the acceleration ay:


Check Your Understanding
(The answers are given at the end of the book.)
23.  
A circus performer hangs stationary from a rope. She then begins to climb upward by pulling herself up, hand over hand. When she starts climbing, is the tension in the rope

(a)  
less than,

(b)  
equal to, or

(c)  
greater than it is when she hangs stationary?
24.  
A freight train is accelerating on a level track. Other things being equal, would the tension in the coupling between the engine and the first car change if some of the cargo in the last car were transferred to any one of the other cars?
25.  
Two boxes have masses m1 and m2, and m2 is greater than m1. The boxes are being pushed across a frictionless horizontal surface. As the drawing shows, there are two possible arrangements, and the pushing force is the same in each. In which arrangement, (a) or (b), does the force that the left box applies to the right box have a greater magnitude, or (c) is the magnitude the same in both cases?




Copyright © 2010 John Wiley & Sons, Inc. All rights reserved.