Concepts & Calculations

Newton's three laws of motion provide the basis for understanding the effect of forces on the motion of an object, as we have seen. The second law is especially important, because it provides the quantitative relationship between net force and acceleration. The examples in this section serve as a review of the essential features of this relationship.

Concepts & Calculations Example 20 Velocity, Acceleration, and Newton's Second Law of Motion

Figure 4.37 shows two forces,

and

, acting on a spacecraft; the plus signs indicate that the forces are directed along the +x axis. A third force

also acts on the spacecraft but is not shown in the drawing. The craft is moving with a constant velocity of +850 m/s. Find the magnitude and direction of

Figure 4.37

Two horizontal forces,

and

, act on the spacecraft. A third force

also acts but is not shown.

	Concept Questions and Answers

Suppose the spacecraft were stationary. What would be the direction of

When the spacecraft is moving at a constant velocity of +850 m/s, what is the direction of

Solution Since the velocity is constant, the acceleration is zero. The net force must also be zero, so that

Solving for F₃ yields

The minus sign in the answer means that

points opposite to the sum of

and

, or along the -x axis in Figure 4.37. The force

has a magnitude of 8000 N, which is the magnitude of the sum of the forces

and

. The answer is independent of the velocity of the spacecraft, as long as that velocity remains constant.

Concepts & Calculations Example 21 The Importance of Mass

On earth a block has a weight of 88 N. This block is sliding on a horizontal surface on the moon, where the acceleration due to gravity is 1.60 m/s². As Figure 4.38a shows, the block is being pulled by a horizontal rope in which the tension is T = 24 N. The coefficient of kinetic friction between the block and the surface is μ_k = 0.20. Determine the acceleration of the block.

Figure 4.38

(a)

A block is sliding on a horizontal surface on the moon. The tension in the rope is .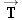

(b)

The free-body diagram for the block, including a kinetic frictional force .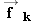

	Concept Questions and Answers

Which of Newton's laws of motion provides a way to determine the acceleration of the block?

This problem deals with a situation on the moon, but the block's mass on the moon is not given. Instead, the block's earth-weight is given. Why can the earth-weight be used to obtain a value for the block's mass that applies on the moon?

Does the net force ΣF_x equal the tension T?

Solution Figure 4.38b shows the free-body diagram for the block. The net force along the x axis is ΣF_x = +T - f_k, where T is the magnitude of the tension in the rope and f_k is the magnitude of the kinetic frictional force. According to Equation 4.8, f_k is related to the magnitude F_N of the normal force by f_k = μ_kF_N, where μ_k is the coefficient of kinetic friction. The acceleration a_x of the block is given by Newton's second law as

We can obtain an expression for F_N by noting that the block does not move in the y direction, so a_y = 0 m/s². Therefore, the net force ΣF_y along the y direction must also be zero. An examination of the free-body diagram reveals that ΣF_y = +F_N - mg_moon = 0, so that F_N = mg_moon. The acceleration in the x direction becomes

Using the earth-weight of the block to determine its mass, we find

The acceleration of the block is, then,