|
Newton's Third Law of Motion |
 |
 |
The third law is often called the “action–reaction” law, because it is sometimes quoted as follows: “For every action (force)
there is an equal, but opposite, reaction.”
Figure
4.7 illustrates how the third law applies to an astronaut who is drifting just outside a spacecraft and who pushes on the spacecraft
with a force
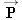
. According to the third law, the spacecraft pushes back on the astronaut with a force
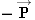
that is equal in magnitude but opposite in direction. In Example
4, we examine the accelerations produced by each of these forces.
 |
 |
|
|
 |

|
Figure 4.7 |
The astronaut pushes on the spacecraft with a force 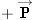 . According to Newton's third law, the spacecraft simultaneously pushes back on the astronaut with a force . According to Newton's third law, the spacecraft simultaneously pushes back on the astronaut with a force 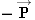 . .
|
|
 |
|
 |
 |
 |
 |
Example 4 The Accelerations Produced by Action and Reaction Forces |
|
 |
 |
 |
 |
|
Suppose that the mass of the spacecraft in Figure 4.7 is mS = 11 000 kg and that the mass of the astronaut is mA = 92 kg. In addition, assume that the astronaut exerts a force of 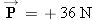 on the spacecraft. Find the accelerations of the spacecraft and the astronaut.
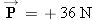 to the spacecraft, the spacecraft applies a reaction force to the spacecraft, the spacecraft applies a reaction force 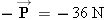 to the astronaut. As a result, the spacecraft and the astronaut accelerate in opposite directions. Although the action and
reaction forces have the same magnitude, they do not create accelerations of the same magnitude, because the spacecraft and
the astronaut have different masses. According to Newton's second law, the astronaut, having a much smaller mass, will experience
a much larger acceleration. In applying the second law, we note that the net force acting on the spacecraft is to the astronaut. As a result, the spacecraft and the astronaut accelerate in opposite directions. Although the action and
reaction forces have the same magnitude, they do not create accelerations of the same magnitude, because the spacecraft and
the astronaut have different masses. According to Newton's second law, the astronaut, having a much smaller mass, will experience
a much larger acceleration. In applying the second law, we note that the net force acting on the spacecraft is 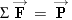 , while the net force acting on the astronaut is , while the net force acting on the astronaut is 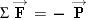 . .
Solution
 |
|
|
 |
|
Even though the magnitudes of the action and reaction forces are always equal, these forces do not necessarily produce accelerations
that have equal magnitudes, since each force acts on a different object that may have a different mass.
|
|
|
Using the second law, we find that the acceleration of the spacecraft is
The acceleration of the astronaut is
|
 |
 |
|
 |
 |
|
 |
 |
 |
 |
 |
 |
| Copyright © 2010 John Wiley & Sons, Inc. All rights reserved. |


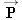 . According to the third law, the spacecraft pushes back on the astronaut with a force
. According to the third law, the spacecraft pushes back on the astronaut with a force 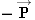 that is equal in magnitude but opposite in direction. In Example 4, we examine the accelerations produced by each of these forces.
that is equal in magnitude but opposite in direction. In Example 4, we examine the accelerations produced by each of these forces.



