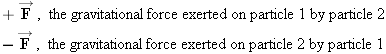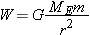The Gravitational Force

Newton's Law of Universal Gravitation

Objects fall downward because of gravity, and Chapters 2 and 3 discuss how to describe the effects of gravity by using a value of g = 9.80 m/s2 for the downward acceleration it causes. However, nothing has been said about why g is 9.80 m/s2. The reason is fascinating, as we will see later in this section.

The acceleration due to gravity is like any other acceleration, and Newton's second law indicates that it must be caused by a net force. In addition to his famous three laws of motion, Newton also provided a coherent understanding of the gravitational force. His “law of universal gravitation” is stated as follows:
Newton's Law of Universal Gravitation
Every particle in the universe exerts an attractive force on every other particle. A particle is a piece of matter, small enough in size to be regarded as a mathematical point. For two particles that have masses m1 and m2 and are separated by a distance r, the force that each exerts on the other is directed along the line joining the particles (see Figure 4.9) and has a magnitude given by

  (4.3)
The symbol G denotes the universal gravitational constant, whose value is found experimentally to be
Figure zoom   Figure 4.9    The two particles, whose masses are m1 and m2, are attracted by gravitational forces and .

The constant G that appears in Equation 4.3 is called the universal gravitational constant, because it has the same value for all pairs of particles anywhere in the universe, no matter what their separation. The value for G was first measured in an experiment by the English scientist Henry Cavendish (1731–1810), more than a century after Newton proposed his law of universal gravitation.

To see the main features of Newton's law of universal gravitation, look at the two particles in Figure 4.9. They have masses m1 and m2 and are separated by a distance r. In the picture, it is assumed that a force pointing to the right is positive. The gravitational forces point along the line joining the particles and are
These two forces have equal magnitudes and opposite directions. They act on different bodies, causing them to be mutually attracted. In fact, these forces are an action–reaction pair, as required by Newton's third law. Example 5 shows that the magnitude of the gravitational force is extremely small for ordinary values of the masses and the distance between them.
Example  5  Gravitational Attraction
What is the magnitude of the gravitational force that acts on each particle in Figure 4.9, assuming m1 = 12 kg (approximately the mass of a bicycle), m2 = 25 kg, and r = 1.2 m?

Reasoning and Solution   The magnitude of the gravitational force can be found using Equation 4.3:
For comparison, you exert a force of about 1 N when pushing a doorbell, so that the gravitational force is exceedingly small in circumstances such as those here. This result is due to the fact that G itself is very small. However, if one of the bodies has a large mass, like that of the earth (5.98 × 1024 kg), the gravitational force can be large.


As expressed by Equation 4.3, Newton's law of gravitation applies only to particles. However, most familiar objects are too large to be considered particles. Nevertheless, the law of universal gravitation can be applied to such objects with the aid of calculus. Newton was able to prove that an object of finite size can be considered to be a particle for purposes of using the gravitation law, provided the mass of the object is distributed with spherical symmetry about its center. Thus, Equation 4.3 can be applied when each object is a sphere whose mass is spread uniformly over its entire volume. Figure 4.10 shows this kind of application, assuming that the earth and the moon are such uniform spheres of matter. In this case, r is the distance between the centers of the spheres and not the distance between the outer surfaces. The gravitational forces that the spheres exert on each other are the same as if the entire mass of each were concentrated at its center. Even if the objects are not uniform spheres, Equation 4.3 can be used to a good degree of approximation if the sizes of the objects are small relative to the distance of separation r.
Figure zoom   Figure 4.10    The gravitational force that each uniform sphere of matter exerts on the other is the same as if each sphere were a particle with its mass concentrated at its center. The earth (mass ME) and the moon (mass MM) approximate such uniform spheres.

Weight

The weight of an object exists because of the gravitational pull of the earth, according to the following definition:
Definition of Weight
The weight of an object on or above the earth is the gravitational force that the earth exerts on the object. The weight always acts downward, toward the center of the earth. On or above another astronomical body, the weight is the gravitational force exerted on the object by that body.

SI Unit of Weight: newton (N)

Using W for the magnitude of the weight,* m for the mass of the object, and ME for the mass of the earth, it follows from Equation 4.3 that

  (4.4)
Equation 4.4 and Figure 4.11 both emphasize that an object has weight whether or not it is resting on the earth's surface, because the gravitational force is acting even when the distance r is not equal to the radius RE of the earth. However, the gravitational force becomes weaker as r increases, since r is in the denominator of Equation 4.4. Figure 4.12, for example, shows how the weight of the Hubble Space Telescope becomes smaller as the distance r from the center of the earth increases. In Example 6 the telescope's weight is determined when it is on earth and in orbit.
Figure zoom   Figure 4.11    On or above the earth, the weight of an object is the gravitational force exerted on the object by the earth.
Example  6  The Hubble Space Telescope
The mass of the Hubble Space Telescope is 11 600 kg. Determine the weight of the telescope (a) when it was resting on the earth and (b) as it is in its orbit 598 km above the earth's surface.
Figure zoom   Figure 4.12    The weight of the Hubble Space Telescope decreases as the telescope gets farther from the earth. The distance from the center of the earth to the telescope is r.
Reasoning   The weight of the Hubble Space Telescope is the gravitational force exerted on it by the earth. According to Equation 4.4, the weight varies inversely as the square of the radial distance r. Thus, we expect the telescope's weight on the earth's surface (r smaller) to be greater than its weight in orbit (r larger).

Solution  
Problem-solving insight
When applying Newton's gravitation law to uniform spheres of matter, remember that the distance r is between the centers of the spheres, not between the surfaces.

(a)  
On the earth's surface, the weight is given by Equation 4.4 with r = 6.38 × 106 m (the earth's radius):
(b)  
When the telescope is 598 km above the surface, its distance from the center of the earth is
The weight now can be calculated as in part (a), except that the new value of r must be used: . As expected, the weight is less in orbit.


The space age has forced us to broaden our ideas about weight. For instance, an astronaut weighs only about one-sixth as much on the moon as on the earth. To obtain his weight on the moon from Equation 4.4, it is only necessary to replace ME by MM (the mass of the moon) and let r = RM (the radius of the moon).

Relation Between Mass and Weight

Problem-solving insight
Mass and weight are different quantities. They cannot be interchanged when solving problems.
Although massive objects weigh a lot on the earth, mass and weight are not the same quantity. As Section 4.2 discusses, mass is a quantitative measure of inertia. As such, mass is an intrinsic property of matter and does not change as an object is moved from one location to another. Weight, in contrast, is the gravitational force acting on the object and can vary, depending on how far the object is above the earth's surface or whether it is located near another body such as the moon.

The relation between weight W and mass m can be written in two ways:

  (4.4 4.5)
Equation 4.4 is Newton's law of universal gravitation, and Equation 4.5 is Newton's second law (net force equals mass times acceleration) incorporating the acceleration g due to gravity. These expressions make the distinction between mass and weight stand out. The weight of an object whose mass is m depends on the values for the universal gravitational constant G, the mass ME of the earth, and the distance r. These three parameters together determine the acceleration g due to gravity. The specific value of g = 9.80 m/s2 applies only when r equals the radius RE of the earth. For larger values of r, as would be the case on top of a mountain, the effective value of g is less than 9.80 m/s2. The fact that g decreases as the distance r increases means that the weight likewise decreases. The mass of the object, however, does not depend on these effects and does not change. Conceptual Example 7 further explores the difference between mass and weight.
  Conceptual Example 7  Mass Versus Weight
A vehicle designed for exploring the moon's surface is being tested on earth, where it weighs roughly six times more than it will on the moon. The acceleration of the vehicle along the ground is measured. To achieve the same acceleration on the moon, will the required net force be (a) the same as, (b) greater than, or (c) less than that on earth?

Reasoning   Do not be misled by the fact that the vehicle weighs more on earth. The greater weight occurs only because the mass and radius of the earth are different than the mass and radius of the moon. In any event, in Newton's second law the net force is proportional to the vehicle's mass, not its weight.

Answers (b) and (c) are incorrect.   According to Newton's second law, for a given acceleration, the net force depends only on the mass. If the required net force were greater or smaller on the moon than it is on the earth, the implication would be that the vehicle's mass is different on the moon than it is on earth, which is contrary to fact.

Answer (a) is correct.   The net force required to accelerate the vehicle is specified by Newton's second law as 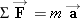, where m is the vehicle's mass and 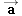is the acceleration. For a given acceleration, the net force depends only on the mass, which is the same on the moon as it is on the earth. Therefore, the required net force is the same on the moon as it is on the earth.

Related Homework:   Problems 21, 26
The Lunar Roving Vehicle that astronaut Eugene Cernan is driving on the moon and the Lunar Excursion Module (behind the Roving Vehicle) have the same mass that they have on the earth. However, their weight is different on the moon than on the earth, as Conceptual Example 7 discusses.
(NASA/Johnson Space Center)

Check Your Understanding
(The answers are given at the end of the book.)
7.  
 
When a body is moved from sea level to the top of a mountain, what changes,

(a)  
the body's mass,

(b)  
its weight, or

(c)  
both its mass and its weight?
8.  
 
Object A weighs twice as much as object B at the same spot on the earth. Would the same be true at a given spot on Mars?
9.  
 
Three particles have identical masses. Each particle experiences only the gravitational forces due to the other two particles. How should the particles be arranged so each one experiences a net gravitational force that has the same magnitude?

(a)  
On the corners of an equilateral triangle,

(b)  
on three of the four corners of a square,

(c)  
on the corners of a right triangle
10.  
 
Two objects with masses m1 and m2 are separated by a distance 2d. Mass m2 is greater than mass m1. A third object has a mass m3. All three objects are located on the same straight line. The net gravitational force acting on the third object is zero. Which one of the drawings correctly represents the locations of the objects?




Copyright © 2010 John Wiley & Sons, Inc. All rights reserved.