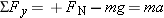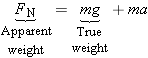|
The Normal Force |
 |
 |
The Definition and Interpretation of the Normal Force
Newton's third law plays an important role in connection with the normal force. In Figure
4.13, for instance, the block exerts a force on the table by pressing down on it. Consistent with the third law, the table exerts
an oppositely directed force of equal magnitude on the block. This reaction force is the normal force. The magnitude of the
normal force indicates how hard the two objects press against each other.
If an object is resting on a horizontal surface and there are no vertically acting forces except the object's weight and the
normal force, the magnitudes of these two forces are equal; that is,
FN =
W. This is the situation in Figure
4.13. The weight must be balanced by the normal force for the object to remain at rest on the table. If the magnitudes of these
forces were not equal, there would be a net force acting on the block, and the block would accelerate either upward or downward,
in accord with Newton's second law.
If other forces in addition to

and
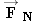
act in the vertical direction, the magnitudes of the normal force and the weight are no longer equal. In Figure
4.14a, for instance, a box whose weight is 15 N is being pushed downward against a table. The pushing force has a magnitude of
11 N. Thus, the total downward force exerted on the box is 26 N, and this must be balanced by the upward-acting normal force
if the box is to remain at rest. In this situation, then, the normal force is 26 N, which is considerably larger than the
weight of the box.
Figure
4.14b illustrates a different situation. Here, the box is being pulled upward by a rope that applies a force of 11 N. The net force
acting on the box due to its weight and the rope is only 4 N, downward. To balance this force, the normal force needs to be
only 4 N. It is not hard to imagine what would happen if the force applied by the rope were increased to 15 N—exactly equal
to the weight of the box. In this situation, the normal force would become zero. In fact, the table could be removed, since
the block would be supported entirely by the rope. The situations in Figure
4.14 are consistent with the idea that the magnitude of the normal force indicates how hard two objects press against each other.
Clearly, the box and the table press against each other harder in part
a of the picture than in part
b.
Like the box and the table in Figure
4.14, various parts of the human body press against one another and exert normal forces. Example
8 illustrates the remarkable ability of the human skeleton to withstand a wide range of normal forces.
 |
 |
 |
Example 8 A Balancing Act |
|
 |
 |
 |
 |
|
Reasoning
To begin, we draw a free-body diagram for the neck and head of the standing performer. Before the act, there are only two
forces, the weight of the standing performer's head and neck, and the normal force. During the act, an additional force is
present due to the woman's weight. In both cases, the upward and downward forces must balance for the head and neck to remain
at rest. This condition of balance will lead us to values for the normal force.
Solution
 |
 |
|
The physics of the human skeleton.
|
|
|
 |
|
(a)
|
Figure 4.15b shows the free-body diagram for the standing performer's head and neck before the act. The only forces acting are the normal
force 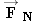 and the 50-N weight. These two forces must balance for the standing performer's head and neck to remain at rest. Therefore,
the seventh cervical vertebra exerts a normal force of  .
|
 |
|
(b)
|
Figure 4.15c shows the free-body diagram that applies during the act. Now, the total downward force exerted on the standing performer's
head and neck is 50 N + 490 N = 540 N, which must be balanced by the upward normal force, so that 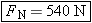 .
|
|
|
 |
 |
|
 |
 |
|
 |
 |
 |
 |
 |
In summary, the normal force does not necessarily have the same magnitude as the weight of the object. The value of the normal
force depends on what other forces are present. It also depends on whether the objects in contact are accelerating. In one
situation that involves accelerating objects, the magnitude of the normal force can be regarded as a kind of “apparent weight,”
as we will now see.
Apparent Weight
Usually, the weight of an object can be determined with the aid of a scale. However, even though a scale is working properly,
there are situations in which it does not give the correct weight. In such situations, the reading on the scale gives only
the “apparent” weight, rather than the gravitational force or “true” weight. The apparent weight is the force that the object
exerts on the scale with which it is in contact.
To see the discrepancies that can arise between true weight and apparent weight, consider the scale in the elevator in Figure
4.16. The reasons for the discrepancies will be explained shortly. A person whose true weight is 700 N steps on the scale. If
the elevator is at rest or moving with a constant velocity (either upward or downward), the scale registers the true weight,
as Figure
4.16a illustrates.
 |
 |
|
|
 |

|
Figure 4.16 |
 |
|
(a)
|
When the elevator is not accelerating, the scale registers the true weight (W = 700 N) of the person.
|
 |
|
(b)
|
When the elevator accelerates upward, the apparent weight (1000 N) exceeds the true weight.
|
 |
|
(c)
|
When the elevator accelerates downward, the apparent weight (400 N) is less than the true weight.
|
 |
|
(d)
|
The apparent weight is zero if the elevator falls freely—that is, if it falls with the acceleration due to gravity.
|
|
|
|
 |
|
 |
If the elevator is accelerating, the apparent weight and the true weight are not equal. When the elevator accelerates upward,
the apparent weight is greater than the true weight, as Figure
4.16b shows. Conversely, if the elevator accelerates downward, as in part
c, the apparent weight is less than the true weight. In fact, if the elevator falls freely, so its acceleration is equal to
the acceleration due to gravity, the apparent weight becomes zero, as part
d indicates. In a situation such as this, where the apparent weight is zero, the person is said to be “weightless.” The apparent
weight, then, does not equal the true weight if the scale and the person on it are accelerating.
The discrepancies between true weight and apparent weight can be understood with the aid of Newton's second law. Figure
4.17 shows a free-body diagram of the person in the elevator. The two forces that act on him are the true weight
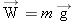
and the normal force
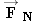
exerted by the platform of the scale. Applying Newton's second law in the vertical direction gives
where
a is the acceleration of the elevator and person. In this result, the symbol
g stands for the magnitude of the acceleration due to gravity and can never be a negative quantity. However, the acceleration
a may be either positive or negative, depending on whether the elevator is accelerating upward (+) or downward (-). Solving
for the normal force
FN shows that
In Equation
4.6,
FN is the magnitude of the normal force exerted on the person by the scale. But in accord with Newton's third law,
FN is also the magnitude of the downward force that the person exerts on the scale—namely, the apparent weight.
 |
 |
|
|
 |

|
Figure 4.17 |
A free-body diagram showing the forces acting on the person riding in the elevator of Figure 4.16. 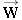 is the true weight, and is the true weight, and 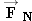 is the normal force exerted on the person by the platform of the scale. is the normal force exerted on the person by the platform of the scale.
|
|
 |
|
 |
Equation
4.6 contains all the features shown in Figure
4.16. If the elevator is not accelerating,
a = 0 m/s
2, and the apparent weight equals the true weight. If the elevator accelerates upward,
a is positive, and the equation shows that the apparent weight is greater than the true weight. If the elevator accelerates
downward,
a is negative, and the apparent weight is less than the true weight. If the elevator falls freely,
a = -
g, and the apparent weight is zero. The apparent weight is zero because when both the person and the scale fall freely, they
cannot push against one another. In this text, when the weight is given, it is assumed to be the true weight, unless stated
otherwise.
 |
 |
 |
Check Your Understanding |
|
 |
 |
 |
 |
|
(The answers are given at the end of the book.)
|
 |
| 11. |
A stack of books whose true weight is 165 N is placed on a scale in an elevator. The scale reads 165 N. From this information
alone, can you tell whether the elevator is moving with a constant velocity of 2 m/s upward, is moving with a constant velocity
of 2 m/s downward, or is at rest?
|
 |
 |
| 12. |
A 10-kg suitcase is placed on a scale that is in an elevator. In which direction is the elevator accelerating when the scale
reads 75 N and when it reads 120 N?
|
(a)
|
Downward when it reads 75 N and upward when it reads 120 N,
|
 |
|
(b)
|
upward when it reads 75 N and downward when it reads 120 N,
|
 |
|
(c)
|
downward in both cases,
|
 |
|
(d)
|
upward in both cases
|
 |
|
 |
 |
| 13. |
You are standing on a scale in an elevator that is moving upward with a constant velocity. The scale reads 600 N. The following
table shows five options for what the scale reads when the elevator slows down as it comes to a stop, when it is stopped,
and when it picks up speed on its way back down. Which one of the five options correctly describes the scale's readings? Note
that the symbol < means “less than” and > means “greater than.”
 |
 |
|
Option
|
Elevator slows down as it comes to a halt
|
Elevator is stopped
|
Elevator picks up speed on its way back down
|
|
(a)
|
> 600 N
|
> 600 N
|
> 600 N
|
|
(b)
|
< 600 N
|
600 N
|
< 600 N
|
|
(c)
|
> 600 N
|
600 N
|
< 600 N
|
|
(d)
|
< 600 N
|
< 600 N
|
< 600 N
|
|
(e)
|
< 600 N
|
600 N
|
> 600 N
|
|
|
|
|
 |
|
 |
|
 |
 |
|
|
 |
 |
|
 |
 |
 |
 |
 |
 |
| Copyright © 2010 John Wiley & Sons, Inc. All rights reserved. |


 and the normal force
and the normal force 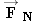 . To understand how an inanimate object, such as a tabletop, can exert a normal force, think about what happens when you sit
on a mattress. Your weight causes the springs in the mattress to compress. As a result, the compressed springs exert an upward
force (the normal force) on you. In a similar manner, the weight of the block causes invisible “atomic springs” in the surface
of the table to compress, thus producing a normal force on the block.
. To understand how an inanimate object, such as a tabletop, can exert a normal force, think about what happens when you sit
on a mattress. Your weight causes the springs in the mattress to compress. As a result, the compressed springs exert an upward
force (the normal force) on you. In a similar manner, the weight of the block causes invisible “atomic springs” in the surface
of the table to compress, thus producing a normal force on the block.
 and
and 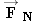 act in the vertical direction, the magnitudes of the normal force and the weight are no longer equal. In Figure 4.14a, for instance, a box whose weight is 15 N is being pushed downward against a table. The pushing force has a magnitude of
11 N. Thus, the total downward force exerted on the box is 26 N, and this must be balanced by the upward-acting normal force
if the box is to remain at rest. In this situation, then, the normal force is 26 N, which is considerably larger than the
weight of the box.
act in the vertical direction, the magnitudes of the normal force and the weight are no longer equal. In Figure 4.14a, for instance, a box whose weight is 15 N is being pushed downward against a table. The pushing force has a magnitude of
11 N. Thus, the total downward force exerted on the box is 26 N, and this must be balanced by the upward-acting normal force
if the box is to remain at rest. In this situation, then, the normal force is 26 N, which is considerably larger than the
weight of the box.


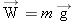 and the normal force
and the normal force 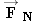 exerted by the platform of the scale. Applying Newton's second law in the vertical direction gives
exerted by the platform of the scale. Applying Newton's second law in the vertical direction gives