Position and Displacement Along a Line

2-2

Constant Velocity

Defining a Coordinate System

In order to study motion along a straight line, we must be able to specify the location of an object and how it changes over time. A convenient way to locate a point of interest or an object is to define a coordinate system. Houses in Costa Rican towns are commonly located with addresses such as “200 meters east of the Post Office.” In order to locate a house, a distance scale must be agreed upon (meters are used in the example), and a reference point or origin (in this case the Post Office), and a direction (in this case east) must be specified. Thus, in locating an object that can move along a straight line, it is convenient to specify its position by choosing a one-dimensional coordinate system. The system consists of a point of reference known as the origin (or zero point), a line that passes through the chosen origin called a coordinate axis, one direction along the coordinate axis, chosen as positive and the other direction as negative, and the units we use to measure a quantity. We have labeled the coordinate axis as the x saxis, in Fig. 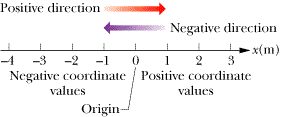2-1, and placed an origin on it. The direction of increasing numbers (coordinates) is called the positive direction, which is toward the right in Fig. 2-1. The opposite direction is the negative direction.

Figure 2-1 Position is determined on an axis that is marked in units of meters and that extends indefinitely in opposite directions.

Figure 2-1 is drawn in the traditional fashion, with negative coordinates to the left of the origin and positive coordinates to the right. It is also traditional in physics to use meters as the standard scale for distance. However, we have freedom to choose other units and to decide which side of the origin is labeled with negative coordinates and which is labeled with positive coordinates. Furthermore, we can choose to define an x axis that is vertical rather than horizontal, or inclined at some angle. In short, we are free to make choices about how we define our coordinate system.

Good choices make describing a situation much easier. For example, in our consideration of motion along a straight line, we would want to align the axis of our one-dimensional coordinate system along the line of motion. In Chapters 5 and 6, when we consider motions in two dimensions, we will be using more complex coordinate systems with a set of mutually perpendicular coordinate axes. Choosing a coordinate system that is appropriate to the physical situation being described can simplify your mathematical description of the situation. To describe a particle moving in a circle, you would probably choose a two-dimensional coordinate system in the plane of the circle with the origin placed at its center.

Defining Position as a Vector Quantity

The reason for choosing our standard one-dimensional coordinate axis and orienting it along the direction of motion is to be able to define the position of an object relative to our chosen origin, and then be able to keep track of how its position changes as the object moves. It turns out that the position of an object relative to a coordinate system can be described by a mathematical entity known as a vector. This is because, in order to find the position of an object, we must specify both how far and in which direction the object is from the origin of a coordinate system.

A VECTOR is a mathematical entity that has both a magnitude and a direction. Vectors can be added, subtracted, multiplied, and transformed according to well-defined mathematical rules.

There are other physical quantities that also behave like vectors such as velocity, acceleration, force, momentum, and electric and magnetic fields.

However, not all physical quantities that have signs associated with them are vectors. For example, temperatures do not need to be described in terms of a coordinate system, and single numbers, such as T = –5°C or T = 12°C, are sufficient to describe them. The minus sign, in this case, does not signify a direction. Mass, distance, length, area, and volume also have no directions associated with them and, although their values depend on the units used to measure them, their values do not depend on the orientation of a coordinate system. Such quantities are called scalars.

A SCALAR is defined as a mathematical quantity whose value does not depend on the orientation of a coordinate system and has no direction associated with it.

In general, a one-dimensional vector can be represented by an arrow. The length of the arrow, which is inherently positive, represents the magnitude of the vector and the direction in which the arrow points represents the direction associated with the vector.

We begin this study of motion by introducing you to the properties of one dimensional position and displacement vectors and some of the formal methods for representing and manipulating them. These formal methods for working with vectors will prove to be very useful later when working with two- and three-dimensional vectors.

A one-dimensional position vector is defined by the location of the origin of a chosen one-dimensional coordinate system and of the object of interest. The magnitude of the position vector is a scalar that denotes the distance between the object and the origin. For example, an object that has a position vector of magnitude 5 m could be located at the point +5 m or –5 m from the origin.

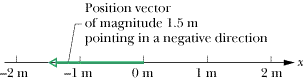On a conventional x axis, the direction of the position vector is positive when the object is located to the right of the origin and negative when the object is located to the left of the origin. For example, in the system shown in Fig. 2-1, if a particle is located at a distance of 3 m to the left of the origin, its position vector has a magnitude of 3 m and a direction that is negative. One of many ways to represent a position vector is to draw an arrow from the origin to the object's location, as shown in Fig. 2-2, for an object that is 1.5 m to the left of the origin. Since the length of a vector arrow represents the magnitude of the vector, its length should be proportional to the distance from the origin to the object of interest. In addition, the direction of the arrow should be from the origin to the object.

Figure 2-2 A position vector can be represented by an arrow pointing from the origin of a chosen coordinate system to the location of the object.

Instead of using an arrow, a position vector can be represented mathematically. In order to develop a useful mathematical representation we need to define a unit vector associated with our x axis.

A UNIT VECTOR FOR A COORDINATE AXIS is a dimensionless vector that points in the direction along a coordinate axis that is chosen to be positive.

It is customary to represent a unit vector that points along the positive x axis with the symbol 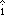(i-hat), although some texts use the symbol 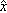(x-hat) instead. When considering three-dimensional vectors, the unit vectors pointing along the designated positive y axis and z axis are denoted by 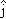and 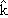, respectively.

These vectors are called “unit vectors” because they have a dimensionless value of one. However, you should not confuse the use of word “unit” with a physical unit. Unit vectors should be shown on coordinate axes as small pointers with no physical units, such as meters, associated with them. This is shown in Fig. 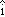2-3 for the x axis unit vector. Since the scale used in the coordinate system has units, it is essential that the units always be associated with the number describing the location of an object along an axis. Figure 2-3 also shows how the unit vector is used to create a position vector corresponding to an object located at position –1.5 meters on our x axis. To do this we stretch or multiply the unit vector by the magnitude of the position vector, which is 1.5 m. Note that we are using the coordinate axis to describe a position in meters relative to an origin, so it is essential to include the units with the number. This multiplication of the dimensionless unit vector by 1.5 m creates a 1.5-m-long vector that points in the same direction as the unit vector. It is denoted by (1.5 m). However, the vector we want to create points in the negative direction, so the vector pointing in the positive direction must be inverted using a minus sign. The position vector we have created is denoted as 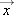. It can be divided into two parts—a vector component and a unit vector,

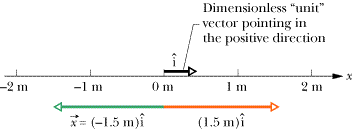Figure 2-3 Arrows representing: (1) a dimensionless unit vector,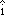

, pointing in the positive x direction; (2) a vector representing the unit vector multiplied by 1.5 meters; and (3) a vector multiplied by 1.5 meters and inverted by multiplication by –1 to create the position vector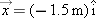

. This position vector has a magnitude of 1.5 meters and points in a negative direction.

In this example, the x-component of the position vector, denoted as x, is –1.5 m.

Here the quantity 1.5 m with no minus sign in front of it is known as the magnitude of this position vector. In general, the magnitude is denoted as . Thus, the one-dimensional position vector for the situation shown in Fig. 2-3 is denoted mathematically using the following symbols:

The x-component of a position vector, denoted x, can be positive or negative depending on which side of the origin the particle is. Thus, in one dimension in terms of absolute values, the vector component x is eithe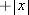r or 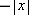, depending on the object's location.

In general, a component of a vector along an axis, such as x in this case, is not a scalar since our x-component will change sign if we choose to reverse the orientation of our chosen coordinate system. In contrast, the magnitude of a position vector is always positive, and it only tells us how far away the object is from the origin, so the magnitude of a vector is always a scalar quantity. The sign of the component (+ or –) tells us in which direction the vector is pointing.The sign will be negative if the object is to the left of the origin and positive if it is to the right of the origin.

Defining Displacement as a Vector Quantity

The study of motion is primarily about how an object's location changes over time under the influence of forces. In physics the concept of change has an exact mathematical definition.

CHANGE is defined as the difference between the state of a physical system (typically called the final state) and its state at an earlier time (typically called the initial state).

This definition of change is used to define displacement.

DISPLACEMENT is defined as the change of an object's position that occurs during a period of time.

Since position can be represented as a vector quantity, displacement is the difference between two vectors, and thus, is also a vector. So, in the case of motion along a line, an object moving from an “initial” position 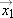to another “final” position 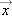at a later time is said to undergo a displacement 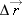, given by the difference of two position vectors

(2-1)

where the symbol D is used to represent a change in a quantity, and the symbol “≡” signifies that the displacement

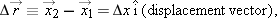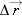is given by

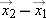because we have chosen to define it that way.

As you will see when we begin to work with vectors in two and three dimensions, it is convenient to consider subtraction as the addition of one vector to another that has been inverted by multiplying the vector component by –1. We can use this idea of defining subtraction as the addition of an inverted vector to find displacements. Let's consider three situations:

(a)

A particle moves along a line from to . Since ,

The positive result indicates that the motion is in the positive direction (toward the right in Fig. 2-4a).

(b)

A particle moves from to . Since ,

The negative result indicates that the displacement of the particle is in the negative direction (toward the left in Fig. 2-4b).

(c)

A particle starts at 5 m, moves to 2 m, and then returns to 5 m. The displacement for the full trip is given by , where and :

and the particle's position hasn't changed, as in Fig. 2-4c. Since displacement involves only the original and final positions, the actual number of meters traced out by the particle while moving back and forth is immaterial.

Figure 2-4 The wide arrow shows the displacement vector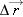

for three situations leading to: (a) a positive displacement, (b) a negative displacement, and (c) zero displacement.

If we ignore the sign of a particle's displacement (and thus its direction), we are left with the magnitude of the displacement. This is the distance between the original and final positions and is always positive. It is important to remember that displacement (or any other vector) has not been completely described until we state its direction.

We use the notation for displacement because when we have motion in more than one dimension, the notation for the position vector is 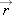. For a one-dimensional motion along a straight line, we can also represent the displacement as . The magnitude of displacement is represented by surrounding the displacement vector symbol with absolute value signs:


READING EXERCISE 2-3:		Can a particle that moves from one position with a negative value, to another position with a negative value, undergo a positive displacement?

TOUCHSTONE EXAMPLE 2-1: Displacements

Three pairs of initial and final positions along an x axis represent the location of objects at two successive times: (pair 1) –3 m, +5 m; (pair 2) –3 m, –7 m; (pair 3) 7 m, –3 m.

(a) Which pairs give a negative displacement?

SOLUTION: The Key Idea here is that the displacement is negative when the final position lies to the left of the initial position. As shown in Fig. 2-5, this happens when the final position is more negative than the initial position. Looking at pair 1, we see that the final position, +5 m, is positive while the initial position, –3 m, is negative. This means that the displacement is from left (more negative) to right (more positive) and so the displacement is positive for pair 1. (Answer)

Figure 2-5 Displacement associated with three pairs of initial and final positions along an x axis.

For pair 2 the situation is different. The final position, –7 m, lies to the left of the initial position,–3 m, so the displacement is negative. (Answer)

For pair 3 the final position, –3 m, is to the left of the origin while the initial position, +7 m, is to the right of the origin. So the displacement is from the right of the origin to its left, a negative displacement. (Answer)

. (b) Calculate the value of the displacement in each case using vector notation.

SOLUTION: The Key Idea here is to use Eq. 2-1 to calculate the displacement for each pair of positions. It tells us the difference between the final position and the initial position, in that order,

(2-2)

For pair 1 the final position is and the initial position is , so the displacement between these two positions is just

(Answer)

For pair 2 the same argument yields

(Answer)

Finally, the displacement for pair 3 is

(Answer)

. (c) What is the magnitude of each position vector?

SOLUTION: Of the six position vectors given, one of them—namely —appears in all three pairs. The remaining three positions are , , and . The Key Idea here is that the magnitude of a position vector just tells us how far the point lies from the origin without regard to whether it lies to the left or to the right of the origin. Thus the magnitude of our first position vector is 3 m (Answer) since the position specified by is 3 m to the left of the origin. It's not –3 m, because magnitudes only specify distance from the origin, not direction.

For the same reason, the magnitude of the second position vector is just 5 m (Answer) while the magnitude of the third and the fourth are each 7 m. (Answer) The fact that the third point lies 7 m to the left of the origin while the fourth lies 7 m to the right doesn't matter here.

. (d) What is the value of the x-component of each of these position vectors?

SOLUTION: To answer this question you need to remember what is meant by the component of a vector. The key equation relating a vector in one dimension to its component along its direction is , where (with the arrow over it) is the vector itself and x (with no arrow over it) is the component of the vector in the direction specified by the unit vector . So the component of is –3 m, while that of is just +5 m, and has as its component along the direction (–7 m) while for it's just (+7 m). In other words, the component of a vector in the direction of is just the signed number (with its units) that multiplies . (Answer)