| Problems |
 |
In several of the problems that follow you are asked to graph position, velocity, and acceleration versus time. Usually a sketch will suffice, appropriately labeled and with straight and curved portions apparent. If you have a computer or graphing calculator, you might use it to produce the graph.
Velocity and Speed
| 1.
Fastball If a baseball pitcher throws a fastball at a horizontal speed of 160 km/h, how long does the ball take to reach home plate 18.4 m away?
|  | |
| 2.
Fastest Bicycle A world speed record for bicycles was set in 1992 by Chris Huber riding Cheetah, a high-tech bicycle built by three mechanical engineering graduates. The record (average) speed was 110.6 km/h through a measured length of 200.0 m on a desert road. At the end of the run, Huber commented, “Cogito ergo zoom!” (I think, therefore I go fast!) What was Huber's elapsed time through the 200.0 m?
|  | |
| 3.
Auto Trip An automobile travels on a straight road for 40 km at 30 km/h. It then continues in the same direction for another 40 km at 60 km/h. (a) What is the average velocity of the car during this 80 km trip? (Assume that it moves in the positive x direction.) (b) What is the average speed? (c) Graph x vs. t and indicate how the average velocity is found on the graph.
|  | |
4.
Radar Avoidance A top-gun pilot, practicing radar avoidance maneuvers, is manually flying horizontally at 1300 km/h, just 35 m above the level ground. Suddenly, the plane encounters terrain that slopes gently upward at 4.3°, an amount difficult to detect visually (Fig. 2-22). How much time does the pilot have to make a correction to avoid flying into the ground?
|  | |
| 5.
On Interstate 10 You drive on Interstate 10 from San Antonio to Houston, half the time at 55 km/h and the other half at 90 km/h. On the way back you travel half the distance at 55 km/h and the other half at 90 km/h. What is your average speed (a) from San Antonio to Houston, (b) from Houston back to San Antonio, and (c) for the entire trip? (d) What is your average velocity for the entire trip? (e) Sketch x vs. t for (a), assuming the motion is all in the positive x direction. Indicate how the average velocity can be found on the sketch.
|  | |
| 6.
Walk Then Run Compute your average velocity in the following two cases: (a) You walk 73.2 m at a speed of 1.22 m/s and then run 73.2 m at a speed of 3.05 m/s along a straight track. (b) You walk for 1.00 min at a speed of 1.22 m/s and then run for 1.00 min at 3.05 m/s along a straight track. (c) Graph x vs. t for both cases and indicate how the average velocity is found on the graph.
|  | |
7.
Position and Time The position of an object moving along an x axis is given by 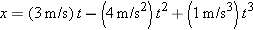 , where x is in meters and t in seconds. (a) What is the position of the object at t = 1, 2, 3, and 4 s? (b) What is the object's displacement between t0 = 0 and t4 = 4 s? (c) What is its average velocity for the time interval from t2 = 2 s to t4 = 4 s? (d) Graph x vs. t for 0 ≤ t ≤ 4 s and indicate how the answer for (c) can be found on the graph. , where x is in meters and t in seconds. (a) What is the position of the object at t = 1, 2, 3, and 4 s? (b) What is the object's displacement between t0 = 0 and t4 = 4 s? (c) What is its average velocity for the time interval from t2 = 2 s to t4 = 4 s? (d) Graph x vs. t for 0 ≤ t ≤ 4 s and indicate how the answer for (c) can be found on the graph.
|  | |
| 8.
Two Trains and a Bird Two trains, each having a speed of 30 km/h, are headed at each other on the same straight track. A bird that can fly 60 km/h flies off the front of one train when they are 60 km apart and heads directly for the other train. On reaching the other train it flies directly back to the first train, and so forth. (We have no idea why a bird would behave in this way.) What is the total distance the bird travels?
|  | |
| 9.
Two Winners On two different tracks, the winners of the 1 kilometer race ran their races in 2 min, 27.95 s and 2 min, 28.15 s. In order to conclude that the runner with the shorter time was indeed faster, how much longer can the other track be in actual length?
|  | |
10.
Scampering Armadillo The graph in Fig. 2-23 is for an armadillo that scampers left (negative direction of x) and right along an x axis. (a) When, if ever, is the animal to the left of the origin on the axis? When, if ever, is its velocity (b) negative, (c) positive, or (d) zero?
|  | |
11.
Position and Time (a) If a particle's position is given by 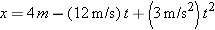 (where t is in seconds and x is in meters), what is its velocity at t1 = 1 s? (b) Is it moving in the positive or negative direction of x just then? (c) What is its speed just then? (d) Is the speed larger or smaller at later times? (Try answering the next two questions without further calculation.) (e) Is there ever an instant when the velocity is zero? (f) Is there a time after t3 = 3 s when the particle is moving in the negative direction of x? (where t is in seconds and x is in meters), what is its velocity at t1 = 1 s? (b) Is it moving in the positive or negative direction of x just then? (c) What is its speed just then? (d) Is the speed larger or smaller at later times? (Try answering the next two questions without further calculation.) (e) Is there ever an instant when the velocity is zero? (f) Is there a time after t3 = 3 s when the particle is moving in the negative direction of x?
|  | |
12.
Particle Position and Time The position of a particle moving along the x axis is given in meters by 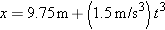 where t is in seconds. Calculate (a) the average velocity during the time interval t = 2.00 s to t = 3.00 s; (b) the instantaneous velocity at t = 2.00 s; (c) the instantaneous velocity at t = 3.00 s; (d) the instantaneous velocity at t = 2.50 s; and (e) the instantaneous velocity when the particle is midway between its positions at t = 2.00 s and t = 3.00 s (f) Graph x vs. t and indicate your answers graphically. where t is in seconds. Calculate (a) the average velocity during the time interval t = 2.00 s to t = 3.00 s; (b) the instantaneous velocity at t = 2.00 s; (c) the instantaneous velocity at t = 3.00 s; (d) the instantaneous velocity at t = 2.50 s; and (e) the instantaneous velocity when the particle is midway between its positions at t = 2.00 s and t = 3.00 s (f) Graph x vs. t and indicate your answers graphically.
|  | |
13.
Velocity–Time Graph How far does the runner whose velocity–time graph is shown in Fig. 2-24 travel in 16 s?
|  | |
Describing Velocity Change
| 14.
Various Motions Sketch a graph that is a possible description of position as a function of time for a particle that moves along the x axis and, at t = 1 s, has (a) zero velocity and positive acceleration; (b) zero velocity and negative acceleration; (c) negative velocity and positive acceleration; (d) negative velocity and negative acceleration. (e) For which of these situations is the speed of the particle increasing at t = 1 s?
|  | |
| 15.
Two Similar Expressions What do the quantities (a) (dx/dt)2 and (b) d2x/dt2 represent? (c) What are their SI units?
|  | |
16.
Frightened Ostrich A frightened ostrich moves in a straight line with velocity described by the velocity–time graph of Fig. 2-25. Sketch acceleration vs. time.
|  | |
| 17.
Speed Then and Now A particle had a speed of 18 m/s at a certain time, and 2.4 s later its speed was 30 m/s in the opposite direction.What were the magnitude and direction of the average acceleration of the particle during this 2.4 s interval?
|  | |
18.
Stand Then Walk From t0 = 0 to t5 = 5.00 min, a man stands still, and from t5 = 5.00 min to t10 = 10.0 min, he walks briskly in a straight line at a constant speed of 2.20 m/s. What are (a) his average velocity 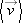 and (b) his average acceleration and (b) his average acceleration 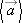 in the time interval 2.00 min to 8.00 min? What are (c) in the time interval 2.00 min to 8.00 min? What are (c) 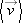 and and 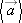 in the time interval 3.00 min to 9.00 min? (e) Sketch x vs. t and v vs. t, and indicate how the answers to (a) through (d) can be obtained from the graphs. in the time interval 3.00 min to 9.00 min? (e) Sketch x vs. t and v vs. t, and indicate how the answers to (a) through (d) can be obtained from the graphs.
|  | |
| 19.
Particle Position and Time The position of a particle moving along the x axis depends on the time according to the equation x = ct2 – bt3, where x is in meters and t in seconds. (a) What units must c and b have? Let their numerical values be 3.0 and 2.0. respectively. (b) At what time does the particle reach its maximum positive x position? From t0 = 0.0 s to t4 = 4.0 s, (c) what distance does the particle move and (d) what is its displacement? At t = 1.0, 2.0, 3.0, and 4.0 s, what are (e) its velocities and (f) its accelerations?
|  | |
Constant Acceleration: A Special Case
| 20.
Driver and Rider An automobile driver on a straight road increases the speed at a constant rate from 25 km/h to 55 km/h in 0.50 min. A bicycle rider on a straight road speeds up at a constant rate from rest to 30 km/h in 0.50 min. Calculate their accelerations.
|  | |
| 21.
Stopping a Muon A muon (an elementary particle) moving in a straight line enters a region with a speed of 5.00 × 106 m/s and then is slowed at the rate of 1.25 × 1014 m/s2. (a) How far does the muon take to stop? (b) Graph x vs. t and v vs. t for the muon.
|  | |
| 22.
Rattlesnake Striking The head of a rattlesnake can accelerate at 50 m/s2 in striking a victim. If a car could do as well, how long would it take to reach a speed of 100 km/h from rest?
|  | |
23.
Accelerating an Electron An electron has a constant acceleration of +3.2 m/s2 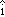 . At a certain instant its velocity is +9.6 m/s . At a certain instant its velocity is +9.6 m/s 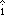 . What is its velocity (a) 2.5 s earlier and (b) 2.5 s later? . What is its velocity (a) 2.5 s earlier and (b) 2.5 s later?
|  | |
| 24.
Speeding Bullet The speed of a bullet is measured to be 640 m/s as the bullet emerges from a barrel of length 1.20 m. Assuming constant acceleration, find the time that the bullet spends in the barrel after it is fired.
|  | |
| 25.
Comfortable Acceleration Suppose a rocket ship in deep space moves with constant acceleration equal to 9.8 m/s2, which gives the illusion of normal gravity during the flight. (a) If it starts from rest, how long will it take to acquire a speed one-tenth that of light, which travels at 3.0 × 108 m/s? (b) How far will it travel in so doing?
|  | |
| 26.
Taking Off A jumbo jet must reach a speed of 360 km/h on the runway for takeoff.What is the least constant acceleration needed for takeoff from a 1.80 km runway?
|  | |
27.
Even Faster Electrons An electron with initial velocity v1 = 1.50 × 105 m/s enters a region 1.0 cm long where it is electrically accelerated (Fig. 2-26). It emerges with velocity v2 = 5.70 × 106 m/s. What is its acceleration, assumed constant? (Such a process occurs in conventional television sets.)
|  | |
| 28.
Stopping Col. Stapp A world's land speed record was set by Colonel John P. Stapp when in March 1954 he rode a rocket-propelled sled that moved along a track at 1020 km/h. He and the sled were brought to a stop in 1.4 s. (See Fig. 2-13) In g units, what acceleration did he experience while stopping?
|  | |
| 29.
Speed Trap The brakes on your automobile are capable of slowing down your car at a rate of 5.2 m/s2. (a) If you are going 137 km/h and suddenly see a state trooper, what is the minimum time in which you can get your car under the 90 km/h speed limit? The answer reveals the futility of braking to keep your high speed from being detected with a radar or laser gun.) (b) Graph x vs. t and v vs. t for such a deceleration.
|  | |
30.
Judging Acceleration Figure 2-27 depicts the motion of a particle moving along an x axis with a constant acceleration. What are the magnitude and direction of the particle's acceleration?
|  | |
| 31.
Hitting a Wall A car traveling 56.0 km/h is 24.0 m from a barrier when the driver slams on the brakes. The car hits the barrier 2.00 s later. (a) What is the car's constant acceleration before impact? (b) How fast is the car traveling at impact?
|  | |
| 32.
Red and Green Trains A red train traveling at 72 km/h and a green train traveling at 144 km/h are headed toward one another along a straight, level track.When they are 950 m apart, each engineer sees the other's train and applies the brakes. The brakes slow each train at the rate of 1.0 m/s2. Is there a collision? If so, what is the speed of each train at impact? If not, what is the separation between the trains when they stop?
|  | |
| 33.
Between Two Points A car moving with constant acceleration covered the distance between two points 60.0 m apart in 6.00 s. Its speed as it passes the second point was 15.0 m/s. (a) What was the speed at the first point? (b) What was the acceleration? (c) At what prior distance from the first point was the car at rest? (d) Graph x vs. t and v vs. t for the car from rest (t0 = 0).
|  | |
| 34.
Chasing a Truck At the instant the traffic light turns green, an automobile starts with a constant acceleration a of 2.2 m/s2. At the same instant a truck, traveling with a constant speed of 9.5 m/s, overtakes and passes the automobile. (a) How far beyond the traffic signal will the automobile overtake the truck? (b) How fast will the car be traveling at that instant?
|  | |
| 35.
Reaction Time To stop a car, first you require a certain reaction time to begin braking; then the car slows under the constant braking. Suppose that the total distance moved by your car during these two phases is 56.7 m when its initial speed is 80.5 km/h, and 24.4 in when its initial speed is 48.3 km/h.What are (a) your reaction time and (b) the magnitude of the acceleration?
|  | |
36.
Avoiding a Collision When a high-speed passenger train traveling at 161 km/h rounds a bend, the engineer is shocked to see that a locomotive has improperly entered onto the track from a siding and is a distance D = 676 m ahead (Fig. 2-28). The locomotive is moving at 29.0 km/h. The engineer of the high-speed train immediately applies the brakes. (a) What must be the magnitude of the resulting constant acceleration if a collision is to be just avoided? (b) Assume that the engineer is at x = 0 when, at t = 0, he first spots the locomotive. Sketch the x(t) curves representing the locomotive and, high-speed train for the situations in which a collision is just avoided and is not quite avoided.
|  | |
| 37.
Going Up An elevator cab in the New York Marquis Marriott has a total run of 190 m. Its maximum speed is 305 m/min. Its acceleration (both speeding up and slowing) has a magnitude of 1.22 m/s2. (a) How far does the cab move while accelerating to full speed from rest? (b) How long does it take to make the nonstop 190 m run, starting and ending at rest?
|  | |
| 38.
Shuffleboard Disk A shuffleboard disk is accelerated at a constant rate from rest to a speed of 6.0 m/s over a 1.8 m distance by a player using a cue. At this point the disk loses contact with the cue and slows at a constant rate of 2.5 m/s2 until it stops. (a) How much time elapses from when the disk begins to accelerate until it stops? (b) What total distance does the disk travel?
|  | |
| 39.
Electric Vehicle An electric vehicle starts from rest and accelerates at a rate of 2.0 m/s2 in a straight line until it reaches a speed of 20 m/s. The vehicle then slows at a constant rate of 1.0 m/s2 until it stops. (a) How much time elapses from start to stop? (b) How far does the vehicle travel from start to stop?
|  | |
40.
Red Car–Green Car In Fig. 2-29 a red car and a green car, identical except for the color, move toward each other in adjacent lanes and parallel to an x axis.At time t = 0, the red car is at x = 0 and the green car is at x = 220 m. If the red car has a constant velocity of 20 km/h, the cars pass each other at x = 44.5 m, and if it has a constant velocity of 40 km/h, they pass each other at x = 76.6 m. What are (a) the initial velocity and (b) the acceleration of the green car?
|  | |
| 41.
Position Function The position of a particle moving along an x axis is given by x = (12 m/s2)t2–(2 m/s3)t3, where x is in meters and t is in seconds. (a) Determine the position, velocity, and acceleration of the particle at t3 = 3.0 s. (b) What is the maximum positive coordinate reached by the particle and at what time is it reached? (c) What is the maximum positive velocity reached by the particle and at what time is it reached? (d) What is the acceleration of the particle at the instant the particle is not moving (other than at t0 = 0)? (e) Determine the average velocity of the particle between t0 = 0 and t3 = 3 s.
|  | |
 |
| Copyright © 2000-2003 by John Wiley & Sons, Inc. or related companies. All rights reserved. |
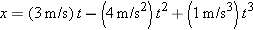 , where x is in meters and t in seconds. (a) What is the position of the object at t = 1, 2, 3, and 4 s? (b) What is the object's displacement between t0 = 0 and t4 = 4 s? (c) What is its average velocity for the time interval from t2 = 2 s to t4 = 4 s? (d) Graph x vs. t for 0 ≤ t ≤ 4 s and indicate how the answer for (c) can be found on the graph.
, where x is in meters and t in seconds. (a) What is the position of the object at t = 1, 2, 3, and 4 s? (b) What is the object's displacement between t0 = 0 and t4 = 4 s? (c) What is its average velocity for the time interval from t2 = 2 s to t4 = 4 s? (d) Graph x vs. t for 0 ≤ t ≤ 4 s and indicate how the answer for (c) can be found on the graph.
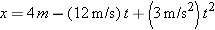 (where t is in seconds and x is in meters), what is its velocity at t1 = 1 s? (b) Is it moving in the positive or negative direction of x just then? (c) What is its speed just then? (d) Is the speed larger or smaller at later times? (Try answering the next two questions without further calculation.) (e) Is there ever an instant when the velocity is zero? (f) Is there a time after t3 = 3 s when the particle is moving in the negative direction of x?
(where t is in seconds and x is in meters), what is its velocity at t1 = 1 s? (b) Is it moving in the positive or negative direction of x just then? (c) What is its speed just then? (d) Is the speed larger or smaller at later times? (Try answering the next two questions without further calculation.) (e) Is there ever an instant when the velocity is zero? (f) Is there a time after t3 = 3 s when the particle is moving in the negative direction of x?
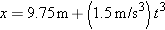 where t is in seconds. Calculate (a) the average velocity during the time interval t = 2.00 s to t = 3.00 s; (b) the instantaneous velocity at t = 2.00 s; (c) the instantaneous velocity at t = 3.00 s; (d) the instantaneous velocity at t = 2.50 s; and (e) the instantaneous velocity when the particle is midway between its positions at t = 2.00 s and t = 3.00 s (f) Graph x vs. t and indicate your answers graphically.
where t is in seconds. Calculate (a) the average velocity during the time interval t = 2.00 s to t = 3.00 s; (b) the instantaneous velocity at t = 2.00 s; (c) the instantaneous velocity at t = 3.00 s; (d) the instantaneous velocity at t = 2.50 s; and (e) the instantaneous velocity when the particle is midway between its positions at t = 2.00 s and t = 3.00 s (f) Graph x vs. t and indicate your answers graphically.
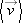 and (b) his average acceleration
and (b) his average acceleration 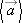 in the time interval 2.00 min to 8.00 min? What are (c)
in the time interval 2.00 min to 8.00 min? What are (c) 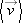 and
and 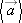 in the time interval 3.00 min to 9.00 min? (e) Sketch x vs. t and v vs. t, and indicate how the answers to (a) through (d) can be obtained from the graphs.
in the time interval 3.00 min to 9.00 min? (e) Sketch x vs. t and v vs. t, and indicate how the answers to (a) through (d) can be obtained from the graphs.
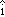 . At a certain instant its velocity is +9.6 m/s
. At a certain instant its velocity is +9.6 m/s 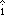 . What is its velocity (a) 2.5 s earlier and (b) 2.5 s later?
. What is its velocity (a) 2.5 s earlier and (b) 2.5 s later?