2-4

Describing Velocity Change

The student shown in Fig. 2-9 is clearly speeding up and slowing down as she walks. We know that the slope of her position vs. time graph over small time intervals keeps changing. Now that we have defined velocity, it is meaningful to develop a mathematical description of how fast velocity changes.We see two approaches to describing velocity change. We could determine velocity change over an interval of displacement magnitude, 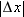, and use 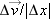as our measure. Alternatively, we could use the ratio of velocity change to the interval of time, Dt, over which the change occurs or 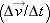. This is analogous to our definition of velocity.

Both of our proposals are possible ways of describing velocity change—neither is right or wrong. In the fourth century B.C.E., Aristotle believed that the ratio of velocity change to distance change was probably constant for any falling objects. Almost 2000 years later, the Italian scientist Galileo did experiments with ramps to slow down the motion of rolling objects. Instead he found that it was the second ratio, 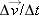, that was constant.

Our modern definition of acceleration is based on Galileo's idea that 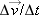is the most useful concept in the description of velocity changes in falling objects.

Whenever a particle's velocity changes, we define it as having an acceleration. The average acceleration, 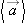, over an interval Dt is defined as

(2-7)

When the particle moves along a line (that is, an x axis in one-dimensional motion),

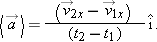It is important to note that an object is accelerated even if all that changes is only the direction of its velocity and not its speed. Directional changes are important as well.

Instantaneous Acceleration

If we want to determine how velocity changes during an instant of time, we need to define instantaneous acceleration (or simply acceleration) in a way that is similar to the way we defined instantaneous velocity:

(2-8)

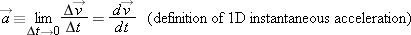In the language of calculus, the ACCELERATION of a particle at any instant is the rate at which its velocity is changing at that instant.

Using this definition, we can determine the acceleration by taking a time derivative of the velocity, 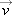. Furthermore, since velocity of an object moving along a line is the derivative of the position, 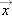, with respect to time, we can write

(2-9)

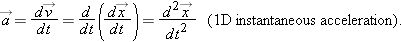Equation 2-9 tells us that the instantaneous acceleration of a particle at any instant is equal to the second derivative of its position, 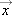, with respect to time. Note that if the object is moving along an x axis, then its acceleration can be expressed in terms of the x-component of its acceleration and the unit vector 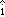along the x axis as

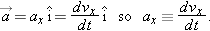Figure 2-12c shows a plot of the x-component of acceleration of an elevator cab. Compare the graph of the x-component of acceleration as a function of time (a_x vs. t) with the graph of the x-component of velocity as a function of time (v_x vs. t) in part b. Each point on the a_x vs. t graph is the derivative (slope or tangent) of the corresponding point on the v_x vs. t graph. When v_x is constant (at either 0 or 4 m/s), its time derivative is zero and hence so is the acceleration.When the cab first begins to move, the v_x vs. t graph has a positive derivative (the slope is positive), which means that a_x is positive. When the cab slows to a stop, the derivative or slope of the v_x vs. t graph is negative; that is, a_x is negative. Next compare the slopes of the v_x vs. t graphs during the two acceleration periods. The slope associated with the cab's stopping is steeper, because the cab stops in half the time it took to get up to speed. The steeper slope means that the magnitude of the stopping acceleration is larger than that of the acceleration as the car is speeding up, as indicated in Fig. 2-12c.

Figure 2-12 (a) The x vs. t graph for an elevator cab that moves upward along an x axis. (b) The v_x vs. t graph for the cab. Note that it is the derivative of the x vs. t graph (v_x = dx/dt). (c) The a_x vs. t graph for the cab. It is the derivative of the v_x vs. t graph (a_x = dv_x/dt). The stick figures along the bottom suggest times that a passenger might feel light and long as the elevator accelerates downward or heavy and squashed as the elevator accelerates upward.

Acceleration has both a magnitude and a direction and so it is a vector quantity. The algebraic sign of its component a_x represents the direction of velocity change along the chosen v_x axis. When acceleration and velocity are in the same direction (have the same sign) the object will speed up. If acceleration and velocity are in opposite directions (and have opposite signs) the object will slow down.

It is important to realize that speeding up is not always associated with an acceleration that is positive. Likewise, slowing down is not always associated with an acceleration that is negative. The relative directions of an object's velocity and acceleration determine whether the object will speed up or slow down.

Since acceleration is defined as any change in velocity over time, whenever an object moving in a straight line has an acceleration it is either speeding up, slowing down, or turning around. Beware! In listening to common everyday language, you will probably hear the word acceleration used only to describe speeding up and the word deceleration to mean slowing down. It's best in studying physics to use the more formal definition of acceleration as a vector quantity that describes both the magnitude and direction of any type of velocity change. In short, an object is accelerating when it is slowing down as well as when it is speeding up.We suggest avoiding the use of the term deceleration while trying to learn the formal language of physics.

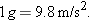The fundamental unit of acceleration must be a velocity (displacement/time) divided by a time, which turns out to be displacement divided by time squared. Displacement is measured in meters and time in seconds in the SI system described in Chapter 1. Thus, the “official” unit of acceleration is m/s². You may encounter other units. For example, large accelerations are often expressed in terms of “g” units where g is directly related to the magnitude of the acceleration of a falling object near the Earth's surface. A g unit is given by

(2-10)

On a roller coaster, you have brief accelerations up to 3g, which, in standard SI units, is (3)(9.8 m/s²) or about 29 m/s². A more extreme example is shown in the photographs of Fig. 2-13, which were taken while a rocket sled was rapidly accelerated along a track and then rapidly braked to a stop.

Figure 2-13 Colonel J.P. Stapp in a rocket sled as it is brought up to high speed (acceleration out of the page) and then very rapidly braked (acceleration into the page).


READING EXERCISE 2-8:		A cat moves along an x axis.What is the sign of its acceleration if it is moving (a) in the positive direction with increasing speed, (b) in the positive direction with decreasing speed, (c) in the negative direction with increasing speed, and (d) in the negative direction with decreasing speed?

TOUCHSTONE EXAMPLE 2-3: Position and Motion

A particle's position on the x axis of Fig. 2-1 is given by

with x in meters and t in seconds.

(a) Find the particle's velocity function and acceleration function .

SOLUTION: One Key Idea is that to get the velocity function , we differentiate the position function x(t) with respect to time. Here we find

(Answer)

with v_x in meters per second.

Another Key Idea is that to get the acceleration function , we differentiate the velocity function with respect to time. This gives us

(Answer)

with a_x in meters per second squared.

. (b) Is there ever a time when

SOLUTION: Setting yields

which has the solution

(Answer)

Thus, the velocity is zero both 3 s before and 3 s after the clock reads 0.

. (c) Describe the particle's motion for

SOLUTION: The Key Idea is to examine the expressions for , , and .

At t = 0, the particle is at and is moving with a velocity of —that is, in the negative direction of the x axis. Its acceleration is , because just then the particle's velocity is not changing.

For , the particle still has a negative velocity, so it continues to move in the negative direction. However, its acceleration is no longer 0 but is increasing and positive. Because the signs of the velocity and the acceleration are opposite, the particle must be slowing.

Indeed, we already know that it turns around at t = 3 s. Just then the particle is as far to the left of the origin in Fig. 2-1 as it will ever get. Substituting t = 3 s into the expression for x(t), we find that the particle's position just then is x = –50 m. Its acceleration is still positive.

For t > 3 s, the particle moves to the right on the axis. Its acceleration remains positive and grows progressively larger in magnitude. The velocity is now positive, and it too grows progressively larger in magnitude.