| 3.9 |
Linear Approximation and the Derivative
|
The Tangent Line Approximation
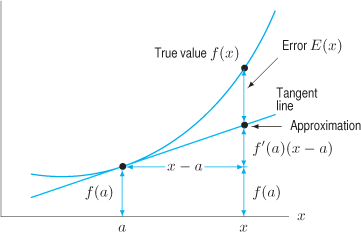
When we zoom in on the graph of a differentiable function, it looks like a straight line. In fact, the graph is not exactly
a straight line when we zoom in; however, its deviation from straightness is so small that it can't be detected by the naked
eye. Let's examine what this means. The straight line that we think we see when we zoom in on the graph of 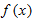 at
at 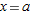 has slope equal to the derivative,
has slope equal to the derivative, 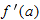 , so the equation is
, so the equation is
The fact that the graph looks like a line means that 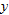 is a good approximation to
is a good approximation to 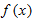 . (See Figure 3.40.) This suggests the following definition:
. (See Figure 3.40.) This suggests the following definition:
It can be shown that the tangent line approximation is the best linear approximation to 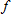 near
near 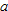 . See Problem 43.
. See Problem 43.
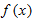 at
at 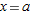 has slope equal to the derivative,
has slope equal to the derivative, 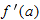 , so the equation is
, so the equation is
|
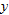 is a good approximation to
is a good approximation to 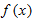 . (See Figure 3.40.) This suggests the following definition:
. (See Figure 3.40.) This suggests the following definition:
|
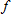 near
near 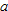 . See Problem 43.
. See Problem 43.
|
|||
|
|
|
Estimating the Error in the Approximation
Let us look at the error, 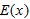 , which is the difference between
, which is the difference between 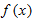 and the local linearization. (Look back at Figure 3.40.) The fact that the graph of
and the local linearization. (Look back at Figure 3.40.) The fact that the graph of 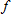 looks like a line as we zoom in means that not only is
looks like a line as we zoom in means that not only is 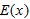 small for
small for  near
near 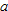 , but also that
, but also that 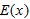 is small relative to
is small relative to 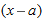 . To demonstrate this, we prove the following theorem about the ratio
. To demonstrate this, we prove the following theorem about the ratio 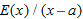 .
.
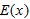 , which is the difference between
, which is the difference between 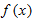 and the local linearization. (Look back at Figure 3.40.) The fact that the graph of
and the local linearization. (Look back at Figure 3.40.) The fact that the graph of 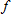 looks like a line as we zoom in means that not only is
looks like a line as we zoom in means that not only is 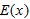 small for
small for  near
near 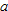 , but also that
, but also that 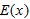 is small relative to
is small relative to 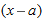 . To demonstrate this, we prove the following theorem about the ratio
. To demonstrate this, we prove the following theorem about the ratio 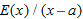 .
.
|
|
Theorem 3.6 says that 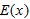 approaches 0 faster than
approaches 0 faster than 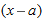 . For the function in Example 3, we see that
. For the function in Example 3, we see that 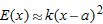 for constant
for constant 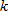 if
if  is near
is near 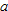 .
.
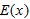 approaches 0 faster than
approaches 0 faster than 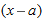 . For the function in Example 3, we see that
. For the function in Example 3, we see that 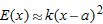 for constant
for constant 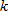 if
if  is near
is near 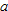 .
.
|
The relationship between 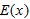 and
and 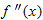 that appears in Example 1 holds more generally. If
that appears in Example 1 holds more generally. If 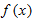 satisfies certain conditions, it can be shown that the error in the tangent line approximation behaves near
satisfies certain conditions, it can be shown that the error in the tangent line approximation behaves near 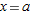 as
as
This is part of a general pattern for obtaining higher-order approximations called Taylor polynomials, which are studied in
Chapter 10.
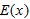 and
and 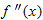 that appears in Example 1 holds more generally. If
that appears in Example 1 holds more generally. If 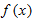 satisfies certain conditions, it can be shown that the error in the tangent line approximation behaves near
satisfies certain conditions, it can be shown that the error in the tangent line approximation behaves near 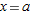 as
as
|
Why Differentiability Makes a Graph Look Straight
We use the properties of the error 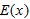 to understand why differentiability makes a graph look straight when we zoom in.
to understand why differentiability makes a graph look straight when we zoom in.
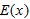 to understand why differentiability makes a graph look straight when we zoom in.
to understand why differentiability makes a graph look straight when we zoom in.
|
We can generalize from this example to explain why differentiability makes the graph of 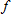 look straight when viewed over a small graphing window. Suppose
look straight when viewed over a small graphing window. Suppose 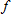 is differentiable at
is differentiable at 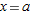 . Then we know
. Then we know 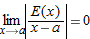 . So, for any
. So, for any  , we can find a δ small enough so that
, we can find a δ small enough so that
So, for any  in the interval
in the interval  , we have
, we have
Thus, the error, 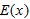 , is less than ε times
, is less than ε times 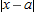 , the distance between
, the distance between  and
and 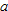 . So, as we zoom in on the graph by choosing smaller ε, the deviation,
. So, as we zoom in on the graph by choosing smaller ε, the deviation, 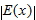 , of
, of 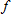 from its tangent line shrinks, even relative to the scale on the
from its tangent line shrinks, even relative to the scale on the 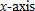 . So, zooming makes a differentiable function look straight.
. So, zooming makes a differentiable function look straight.
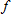 look straight when viewed over a small graphing window. Suppose
look straight when viewed over a small graphing window. Suppose 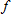 is differentiable at
is differentiable at 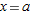 . Then we know
. Then we know 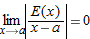 . So, for any
. So, for any  , we can find a δ small enough so that
, we can find a δ small enough so that
|
 in the interval
in the interval  , we have
, we have
|
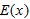 , is less than ε times
, is less than ε times 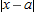 , the distance between
, the distance between  and
and 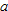 . So, as we zoom in on the graph by choosing smaller ε, the deviation,
. So, as we zoom in on the graph by choosing smaller ε, the deviation, 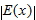 , of
, of 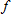 from its tangent line shrinks, even relative to the scale on the
from its tangent line shrinks, even relative to the scale on the 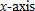 . So, zooming makes a differentiable function look straight.
. So, zooming makes a differentiable function look straight.
Exercises and Problems for Section 3.9
Exercises
| 1. |
Find the tangent line approximation for
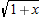 near near 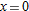 . .
|
| 2. |
What is the tangent line approximation to
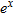 near near 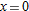 ? ?
|
| 3. |
Find the tangent line approximation to
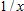 near near 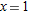 . .
|
| 4. |
Find the local linearization of
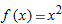 near near 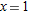 . .
|
| 5. |
What is the local linearization of
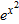 near near 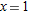 ? ?
|
| 6. |
Show that
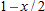 is the tangent line approximation to is the tangent line approximation to 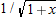 near near 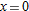 . .
|
| 7. |
Show that
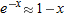 near near 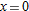 . .
|
| 8. |
Local linearization gives values too small for the function
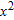 and too large for the function and too large for the function 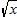 . Draw pictures to explain why. . Draw pictures to explain why.
|
| 9. |
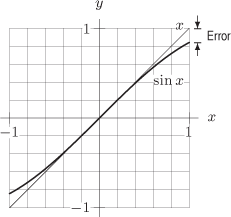
Using a graph like Figure 3.41, estimate to one decimal place the magnitude of the error in approximating sin
 by by  for for 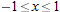 . Is the approximation an over- or an underestimate? . Is the approximation an over- or an underestimate?
|
| 10. |
For
 near 0, local linearization gives near 0, local linearization gives
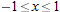 . .
|
Problems
| 11. |
|
| 12. |
|
| 13. |
|
| 14. |
|
| 15. |
Figure 3.43 shows
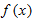 and its local linearization at and its local linearization at 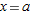 . What is the value of . What is the value of 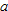 ? Of ? Of 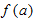 ? Is the approximation an under- or overestimate? Use the linearization to approximate the value of ? Is the approximation an under- or overestimate? Use the linearization to approximate the value of 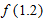 . .
|
In Problems 16-17, the equation has a solution near 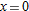 . By replacing the left side of the equation by its linearization, find an approximate value for the solution.
. By replacing the left side of the equation by its linearization, find an approximate value for the solution.
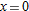 . By replacing the left side of the equation by its linearization, find an approximate value for the solution.
. By replacing the left side of the equation by its linearization, find an approximate value for the solution.
| 16. |
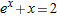 |
| 17. |
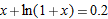 |
| 18. |
|
| 19. |
|
| 20. |
The speed of sound in dry air is
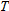 is the temperature in is the temperature in 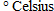 . Find a linear function that approximates the speed of sound for temperatures near . Find a linear function that approximates the speed of sound for temperatures near 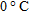 . .
|
| 21. |
Air pressure at sea level is 30 inches of mercury. At an altitude of
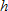 feet above sea level, the air pressure, feet above sea level, the air pressure, 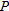 , in inches of mercury, is given by , in inches of mercury, is given by
|
| 22. |
On October 7, 2010, the Wall Street Journal8 reported that Android cell phone users had increased to 10.9 million by the end of August 2010 from 866,000 a year earlier.
During the same period, iPhone users increased to 13.5 million, up from 7.8 million a year earlier. Let
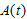 be the number of Android users, in millions, at time t in years since the end of August 2009. Let be the number of Android users, in millions, at time t in years since the end of August 2009. Let 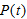 be the number of iPhone users in millions. be the number of iPhone users in millions.
|
| 23. |
Writing
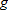 for the acceleration due to gravity, the period, for the acceleration due to gravity, the period, 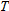 , of a pendulum of length , of a pendulum of length 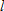 is given by is given by
|
| 24. |
Suppose now the length of the pendulum in Problem 23 remains constant, but that the acceleration due to gravity changes.
|
| 25. |
Suppose
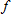 has a continuous positive second derivative for all has a continuous positive second derivative for all  . Which is larger, . Which is larger,  or or 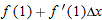 ? Explain. ? Explain.
|
| 26. |
Suppose
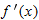 is a differentiable decreasing function for all is a differentiable decreasing function for all  . In each of the following pairs, which number is the larger? Give a reason for your answer. . In each of the following pairs, which number is the larger? Give a reason for your answer.
|
Problems 27-29 investigate the motion of a projectile shot from a cannon. The fixed parameters are the acceleration of gravity,
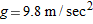 , and the muzzle velocity,
, and the muzzle velocity,  , at which the projectile leaves the cannon. The angle
, at which the projectile leaves the cannon. The angle 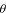 , in degrees, between the muzzle of the cannon and the ground can vary.
, in degrees, between the muzzle of the cannon and the ground can vary.
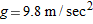 , and the muzzle velocity,
, and the muzzle velocity,  , at which the projectile leaves the cannon. The angle
, at which the projectile leaves the cannon. The angle 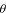 , in degrees, between the muzzle of the cannon and the ground can vary.
, in degrees, between the muzzle of the cannon and the ground can vary.
| 27. |
The range of the projectile is
|
| 28. |
The time that the projectile stays in the air is
|
| 29. |
At its highest point the projectile reaches a peak altitude given by
|
In Problems 30-32, find the local linearization of 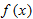 near 0 and use this to approximate the value of
near 0 and use this to approximate the value of 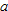 .
.
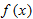 near 0 and use this to approximate the value of
near 0 and use this to approximate the value of 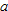 .
.
| 30. |
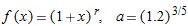 |
| 31. |
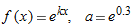 |
| 32. |
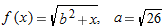 |
In Problems 33-37, find a formula for the error 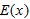 in the tangent line approximation to the function near
in the tangent line approximation to the function near 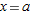 . Using a table of values for
. Using a table of values for 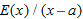 near
near 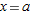 , find a value of
, find a value of 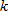 such that
such that 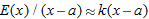 . Check that, approximately,
. Check that, approximately, 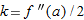 and that
and that 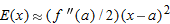 .
.
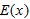 in the tangent line approximation to the function near
in the tangent line approximation to the function near 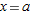 . Using a table of values for
. Using a table of values for 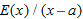 near
near 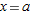 , find a value of
, find a value of 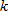 such that
such that 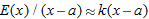 . Check that, approximately,
. Check that, approximately, 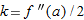 and that
and that 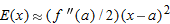 .
.
| 33. |
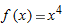 , , 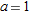 |
| 34. |
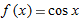 , , 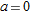 |
| 35. |
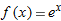 , , 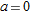 |
| 36. |
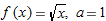 |
| 37. |
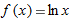 , , 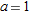 |
| 38. |
Multiply the local linearization of
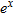 near near 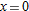 by itself to obtain an approximation for by itself to obtain an approximation for 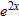 . Compare this with the actual local linearization of . Compare this with the actual local linearization of 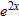 . Explain why these two approximations are consistent, and discuss which one is more accurate. . Explain why these two approximations are consistent, and discuss which one is more accurate.
|
| 39. |
|
| 40. |
From the local linearizations of
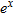 and and 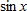 near near 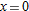 , write down the local linearization of the function , write down the local linearization of the function 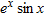 . From this result, write down the derivative of . From this result, write down the derivative of 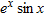 at at 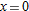 . Using this technique, write down the derivative of . Using this technique, write down the derivative of 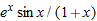 at at 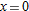 . .
|
| 41. |
Use local linearization to derive the product rule,
|
| 42. |
Derive the chain rule using local linearization.
|
| 43. |
Consider a function
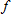 and a point and a point 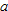 . Suppose there is a number . Suppose there is a number 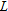 such that the linear function such that the linear function 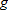
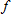 . By good approximation, we mean that . By good approximation, we mean that
 is the approximation error defined by is the approximation error defined by
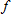 is differentiable at is differentiable at 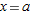 and that and that 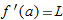 . Thus the tangent line approximation is the only good linear approximation. . Thus the tangent line approximation is the only good linear approximation.
|
| 44. |
Consider the graph of
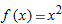 near near 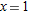 . Find an interval around . Find an interval around 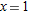 with the property that throughout any smaller interval, the graph of with the property that throughout any smaller interval, the graph of 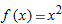 never differs from its local linearization at never differs from its local linearization at 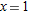 by more than by more than 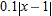 . .
|
Strengthen Your Understanding
In Problems 45-46, explain what is wrong with the statement.
| 45. |
To approximate
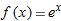 , we can always use the linear approximation , we can always use the linear approximation 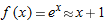 . .
|
| 46. |
The linear approximation for
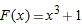 near near 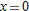 is an underestimate for the function is an underestimate for the function 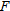 for all for all  , , 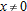 . .
|
In Problems 47-49, give an example of:
| 47. |
Two different functions that have the same linear approximation near
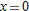 . .
|
| 48. |
A non-polynomial function that has the tangent line approximation
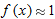 near near 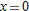 . .
|
| 49. |
A function that does not have a linear approximation at
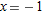 . .
|
| 50. |
Let
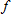 be a differentiable function and let be a differentiable function and let 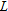 be the linear function be the linear function 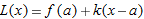 for some constant for some constant 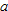 . Decide whether the following statements are true or false for all constants . Decide whether the following statements are true or false for all constants 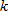 . Explain your answer. . Explain your answer.
|
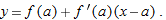
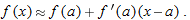
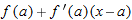 is called the
is called the 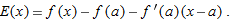
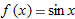 near
near 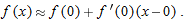
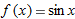 , then
, then 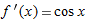 , so
, so 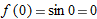 and
and 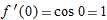 , and the approximation is
, and the approximation is
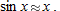
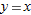 . If we zoom in on the graphs of the functions
. If we zoom in on the graphs of the functions 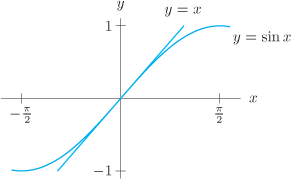

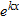 near
near 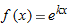 , then
, then 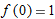 and, by the chain rule,
and, by the chain rule, 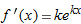 , so
, so 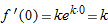 . Thus
. Thus
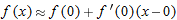
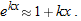
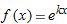 and
and 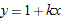 near the origin, we won't be able to tell them apart.
near the origin, we won't be able to tell them apart.
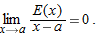
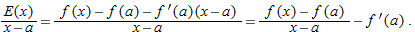
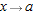 and using the definition of the derivative, we see that
and using the definition of the derivative, we see that
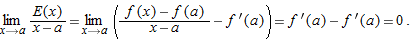
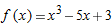 for
for 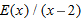 suggest about
suggest about 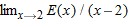 ?
?
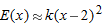 . Estimate the value of
. Estimate the value of 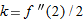 .
.
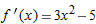 , and
, and 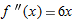 . Thus,
. Thus, 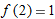 and
and 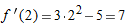 , so the tangent line approximation for
, so the tangent line approximation for 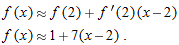
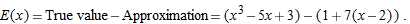
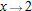 .
.
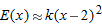 , then
, then 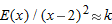 . Thus we make Table
. Thus we make Table 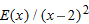 . Since the values are all approximately 6, we guess that
. Since the values are all approximately 6, we guess that 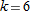 and
and 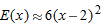 .
.
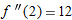 , our value of
, our value of 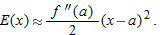
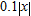 for all
for all 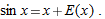
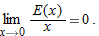
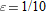 , then the definition of limit guarantees that there is a
, then the definition of limit guarantees that there is a 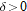 such that
such that
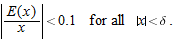
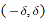 , we have
, we have 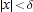 , so
, so
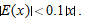
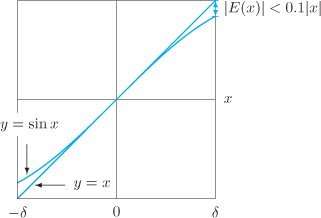
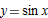 and its linear approximation
and its linear approximation 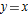 , showing a window in which the magnitude of the error,
, showing a window in which the magnitude of the error,  , is less than
, is less than 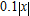 for all
for all 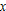 in the window
in the window

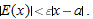

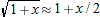

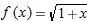 , the chain rule gives
, the chain rule gives 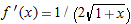 , so
, so 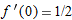 . Therefore the tangent line approximation of
. Therefore the tangent line approximation of 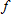 near
near 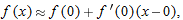
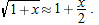
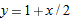 . (See figure
. (See figure 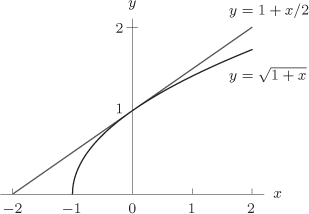
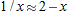
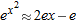
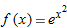 , we get a tangent line approximation of
, we get a tangent line approximation of 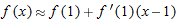 which becomes
which becomes 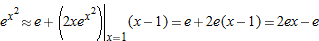 . Thus, our local linearization of
. Thus, our local linearization of  near
near 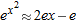 .
.
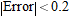
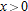
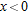
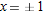 . The magnitude of the error can be read off the graph as less than 0.2 or estimated as
. The magnitude of the error can be read off the graph as less than 0.2 or estimated as
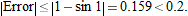
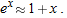
 , to
, to 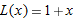
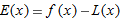 for
for 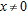

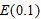 or
or 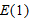 , and why.
, and why.
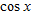 at
at 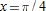 .
.
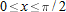 .
.
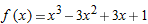 .
.
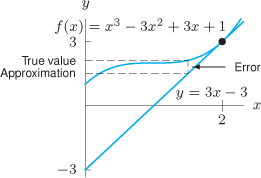
 .
.
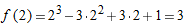 , we have
, we have 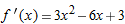 , so
, so 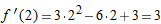 , and the local linearization is
, and the local linearization is 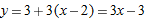 .
.
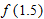 , the tangent line approximation to
, the tangent line approximation to 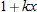 is the local linearization of
is the local linearization of 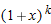 near
near 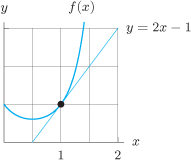
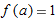
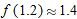
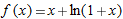 , so
, so 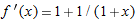 . Thus
. Thus 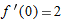 so
so
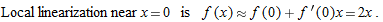
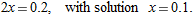
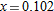 .
.
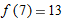 and
and 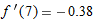 , estimate
, estimate  .
.
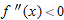 for all
for all 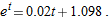
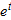 by its linearization near 0. Solve the new equation to get an approximate solution to the original equation.
by its linearization near 0. Solve the new equation to get an approximate solution to the original equation.
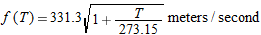
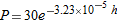
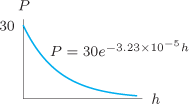
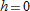 .
.
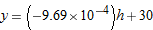
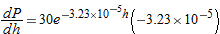
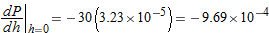
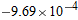 , so the equation of the tangent line is
, so the equation of the tangent line is
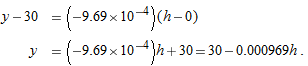
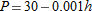
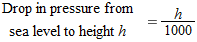
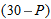 , so
, so
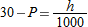

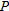 intercepts of 30, and the slopes are almost the same
intercepts of 30, and the slopes are almost the same  . The rule of thumb calculates values of
. The rule of thumb calculates values of  ). Thus, the rule of thumb values are slightly smaller.
). Thus, the rule of thumb values are slightly smaller.
 . Give units.
. Give units.
 . Give units.
. Give units.
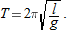
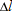 , the change in the period,
, the change in the period, 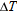 , is given by
, is given by
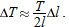
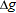 , the change in
, the change in 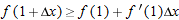
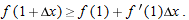
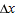 positive, but the result is also true if
positive, but the result is also true if 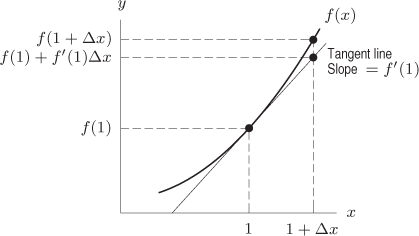
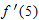 and
and 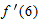
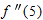 and 0
and 0
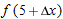 and
and 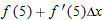
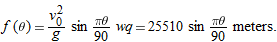
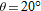 .
.
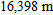
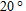 .
.

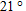 .
.
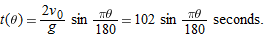
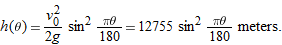
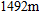
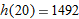 meters
meters

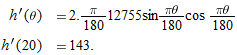
 , near
, near 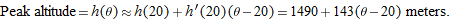
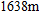
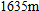
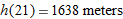 . The linear approximation gives
. The linear approximation gives

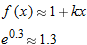
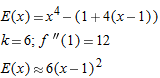
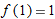 and
and 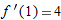 . Thus
. Thus
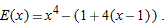
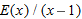 near
near 
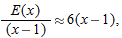
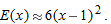
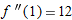 , so
, so
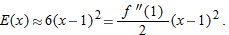
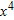 using
using 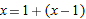 and expanding:
and expanding:


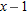 is small, so we ignore powers of
is small, so we ignore powers of 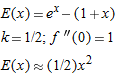
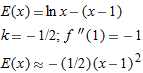
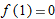 and
and 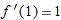 . Thus
. Thus
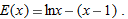
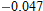
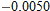
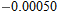
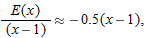
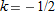 and
and
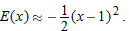
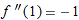 , so
, so
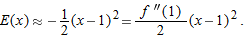
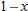 is the local linearization of
is the local linearization of 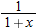 near
near 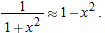
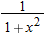 is at
is at 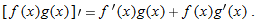

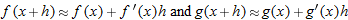 .]
.]
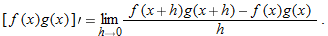
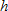 ,
, 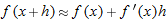 , and
, and 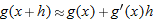 . Therefore
. Therefore
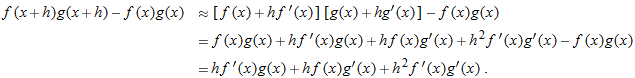
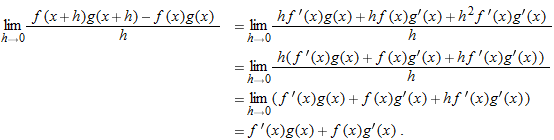
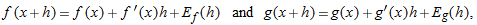
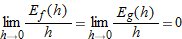 . (This implies that
. (This implies that 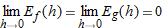 .)
.)
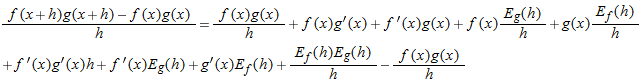
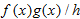 and
and 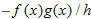 cancel out. All the remaining terms on the right, with the exception of the second and third terms, go to zero as
cancel out. All the remaining terms on the right, with the exception of the second and third terms, go to zero as 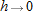 . Thus, we have
. Thus, we have
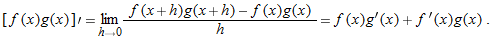
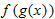 , using
, using 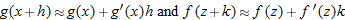 .]
.]
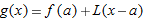
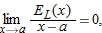
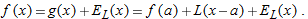
 is the linear approximation for
is the linear approximation for  (instead of 2.718). For
(instead of 2.718). For 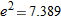 .
.
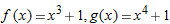
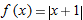
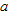 , is given by
, is given by 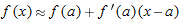 . Since
. Since 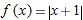 does not have a derivative at
does not have a derivative at 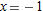 this function does not have a linear approximation for
this function does not have a linear approximation for 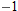 . Other answers are possible.
. Other answers are possible.
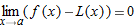 , then
, then