| 2-6 Acceleration | ||
When a particle's velocity changes, the particle is said to undergo acceleration (or to accelerate). For motion along an axis, the average acceleration aavg over a time interval Dt is
|
where the particle has velocity v1 at time t1 and then velocity v2 at time t2. The instantaneous acceleration (or simply acceleration) is the derivative of the velocity with respect to time:
|
In words, the acceleration of a particle at any instant is the rate at which its velocity is changing at that instant. Graphically, the acceleration at any point is the slope of the curve of v(t) at that point.
We can combine Equation 2-8 with Equation 2-4 to write
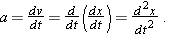 | (2-9) |
In words, the acceleration of a particle at any instant is the second derivative of its position x(t) with respect to time.
A common unit of acceleration is the meter per second per second: m/(s · s) or m/s2. You will see other units in the problems, but they will each be in the form of length/(time · time) or length/time2. Acceleration has both magnitude and direction (it is yet another vector quantity). Its algebraic sign represents its direction on an axis just as for displacement and velocity; that is, acceleration with a positive value is in the positive direction of an axis, and acceleration with a negative value is in the negative direction.
Figure 2-6c is a plot of the acceleration of the elevator cab discussed in Sample Problem 2-2. Compare this a(t) curve with the v(t) curve—each point on the a(t) curve shows the derivative (slope) of the v(t) curve at the corresponding time. When v is constant (at either 0 or 4 m/s), the derivative is zero and so also is the acceleration. When the cab first begins to move, the v(t) curve has a positive derivative (the slope is positive), which means that a(t) is positive. When the cab slows to a stop, the derivative and slope of the v(t) curve are negative; that is, a(t) is negative.
Next compare the slopes of the v(t) curve during the two acceleration periods. The slope associated with the cab's slowing down (commonly called “deceleration”) is steeper because the cab stops in half the time it took to get up to speed. The steeper slope means that the magnitude of the deceleration is larger than that of the acceleration, as indicated in Figure 2-6.
The sensations you would feel while riding in the cab of Figure 2-6 are indicated by the sketched figures at the bottom. When the cab first accelerates, you feel as though you are pressed downward; when later the cab is braked to a stop, you seem to be stretched upward. In between, you feel nothing special. In other words, your body reacts to accelerations (it is an accelerometer) but not to velocities (it is not a speedometer). When you are in a car traveling at 90 km/h or an airplane traveling at 900 km/h, you have no bodily awareness of the motion. However, if the car or plane quickly changes velocity, you may become keenly aware of the change, perhaps even frightened by it. Part of the thrill of an amusement park ride is due to the quick changes of velocity that you undergo (you pay for the accelerations, not for the speed). A more extreme example is shown in the photographs of Figure 2-7, which were taken while a rocket sled was rapidly accelerated along a track and then rapidly braked to a stop.
 |
| Fig. 2-7 Colonel J. P. Stapp in a rocket sled as it is brought up to high speed (acceleration out of the page) and then very rapidly braked (acceleration into the page). |
 |
| Fig. 2-7 Continued |
Large accelerations are sometimes expressed in terms of g units, with
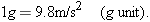 | (2-10) |
(As we shall discuss in Section 2-9, g is the magnitude of the acceleration of a falling object near Earth's surface.) On a roller coaster, you may experience brief accelerations up to 3g, which is (3)(9.8 m/s2), or about 29 m/s2, more than enough to justify the cost of the ride.
| PROBLEM-SOLVING TACTICS |
TACTIC 5: An Acceleration's Sign
In common language, the sign of an acceleration has a nonscientific meaning: positive acceleration means that the speed of an object is increasing, and negative acceleration means that the speed is decreasing (the object is decelerating). In this book, however, the sign of an acceleration indicates a direction, not whether an object's speed is increasing or decreasing.For example, if a car with an initial velocity v = -25 m/s is braked to a stop in 5.0 s, then aavg = +5.0 m/s2. The acceleration is positive, but the car's speed has decreased. The reason is the difference in signs: the direction of the acceleration is opposite that of the velocity.
Here then is the proper way to interpret the signs:
|
If the signs of the velocity and acceleration of a particle are the same, the speed of the particle increases. If the signs are opposite, the speed decreases. |
| CHECKPOINT 4 A wombat moves along an x axis. What is the sign of its acceleration if it is moving (a) in the positive direction with increasing speed, (b) in the positive direction with decreasing speed, (c) in the negative direction with increasing speed, and (d) in the negative direction with decreasing speed? | ||
|
A particle's position on the x axis of Figure 2-1 is given by
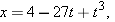 |
with x in meters and t in seconds.
(a) Find the particle's velocity function v(t) and acceleration function a(t).
Solution: One Key Idea is that to get the velocity function v(t), we differentiate the position function x(t) with respect to time. Here we find
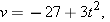 | (Answer) |
with v in meters per second.
Another Key Idea is that to get the acceleration function a(t), we differentiate the velocity function v(t) with respect to time. This gives us
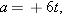 | (Answer) |
with a in meters per second squared.
(b) Is there ever a time when v = 0?
Solution: Setting v(t) = 0 yields
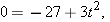 |
which has the solution
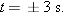 | (Answer) |
Thus, the velocity is zero both 3 s before and 3 s after the clock reads 0.
(c) Describe the particle's motion for t ≥ 0.
Solution: The Key Idea is to examine the expressions for x(t), v(t), and a(t).
At t = 0, the particle is at x(0) = +4 m and is moving with a velocity of v(0) = -27 m/s—that is, in the negative direction of the x axis. Its acceleration is a(0) = 0 because just then the particle's velocity is not changing.
For 0 < t < 3 s, the particle still has a negative velocity, so it continues to move in the negative direction. However, its acceleration is no longer 0 but is increasing and positive. Because the signs of the velocity and the acceleration are opposite, the particle must be slowing.
Indeed, we already know that it stops momentarily at t = 3 s. Just then the particle is as far to the left of the origin in Figure 2-1 as it will ever get. Substituting t = 3 s into the expression for x(t), we find that the particle's position just then is x = -50 m. Its acceleration is still positive.
For t > 3 s, the particle moves to the right on the axis. Its acceleration remains positive and grows progressively larger in magnitude. The velocity is now positive, and it too grows progressively larger in magnitude.