| Sample Problem 2-1 |
|
You drive a beat-up pickup truck along a straight road for 8.4 km at 70 km/h, at which point the truck runs out of gasoline and stops. Over the next 30 min, you walk another 2.0 km farther along the road to a gasoline station.
(a) What is your overall displacement from the beginning of your drive to your arrival at the station?
Solution: Assume, for convenience, that you move in the positive direction of an x axis, from a first position of x1 = 0 to a second position of x2 at the station. That second position must be at x2 = 8.4 km + 2.0 km = 10.4 km. Then the Key Idea here is that your displacement Dx along the x axis is the second position minus the first position. From Equation 2-1, we have
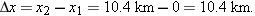 | (Answer) |
Thus, your overall displacement is 10.4 km in the positive direction of the x axis.
(b) What is the time interval Dt from the beginning of your drive to your arrival at the station?
Solution: We already know the walking time interval Dtwlk (= 0.50 h), but we lack the driving time interval Dtdr. However, we know that for the drive the displacement Dxdr is 8.4 km and the average velocity vavg,dr is 70 km/h. A Key Idea to use here comes from Equation 2-2: This average velocity is the ratio of the displacement for the drive to the time interval for the drive:
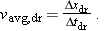 |
Rearranging and substituting data then give us
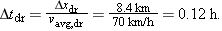 |
So,
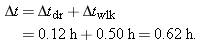 | (Answer) |
(c) What is your average velocity vavg from the beginning of your drive to your arrival at the station? Find it both numerically and graphically.
Solution: The Key Idea here again comes from Equation 2-2: vavg for the entire trip is the ratio of the displacement of 10.4 km for the entire trip to the time interval of 0.62 h for the entire trip. Here we find
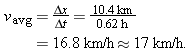 | (Answer) |
To find vavg graphically, first we graph the function x(t) as shown in Figure 2-5, where the beginning and arrival points on the graph are the origin and the point labeled as “Station.” The Key Idea here is that your average velocity is the slope of the straight line connecting those points; that is, vavg is the ratio of the rise (Dx = 10.4 km) to the run (Dt = 0.62 h), which gives us vavg = 16.8 km/h.
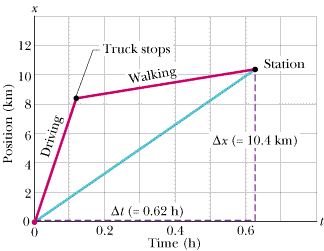 |
| Fig. 2-5 The lines marked “Driving” and “Walking” are the position-time plots for the driving and walking stages. (The plot for the walking stage assumes a constant rate of walking.) The slope of the straight line joining the origin and the point labeled “Station” is the average velocity for the trip, from the beginning to the station. |
(d) Suppose that to pump the gasoline, pay for it, and walk back to the truck takes you another 45 min. What is your average speed from the beginning of your drive to your return to the truck with the gasoline?
Solution: The Key Idea here is that your average speed is the ratio of the total distance you move to the total time interval you take to make that move. The total distance is 8.4 km + 2.0 km + 2.0 km = 12.4 km. The total time interval is 0.12 h + 0.50 h + 0.75 h = 1.37 h. Thus, Equation 2-3 gives us
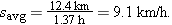 | (Answer) |