(a) The particle is momentarily stopped when its velocity is zero. Its velocity as a function of time is the derivative of its coordinate with respect to time.
(b) Substitute the value for the time of stopping into the function given for the coordinate.
(c) and (d) Put  equal to zero in the given function and solve for
equal to zero in the given function and solve for 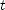 . The equation is quadratic in
. The equation is quadratic in 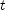 and so has two solutions, one positive and one negative.
and so has two solutions, one positive and one negative.
(f) Suppose the function is  , where
, where  is a constant. This is the same as the original function except it is shifted in time by
is a constant. This is the same as the original function except it is shifted in time by  . if
. if  is positive it is shifted in the positive
is positive it is shifted in the positive 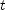 direction and if
direction and if  is negative it is shifted in the negative
is negative it is shifted in the negative 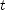 direction. The second function is identical to
direction. The second function is identical to  as you can easily see by squaring the quantity in parentheses.
as you can easily see by squaring the quantity in parentheses.
(g) Set the derivative of the new function equal to zero and solve for 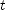 , then substitute back into the function to find the coordinate at which the particle stops.
, then substitute back into the function to find the coordinate at which the particle stops.
[(a) 0; (b) 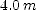 ; (c)
; (c) 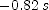 ; (d)
; (d) 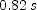 ; (f)
; (f) 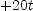 ; (g) increase]
; (g) increase]
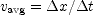 . To calculate the particle's coordinate at the beginning of the interval substitute
. To calculate the particle's coordinate at the beginning of the interval substitute  into the equation for
into the equation for  and to calculate its coordinate at the end of the interval substitute
and to calculate its coordinate at the end of the interval substitute 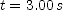 .
. 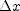 , of course, is the difference and
, of course, is the difference and  is
is 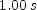
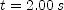 . Do the same for
. Do the same for  and for
and for 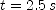 .
.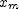 by taking the average of the two coordinates found in part (a), then solve
by taking the average of the two coordinates found in part (a), then solve 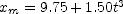 for
for  . Finally, substitute this value for
. Finally, substitute this value for 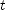 into the expression for the velocity as a function of time (the derivative of the coordinate).
into the expression for the velocity as a function of time (the derivative of the coordinate).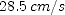 ; (b)
; (b)  ; (c)
; (c) 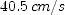 ; (d)
; (d) 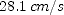 ; (e)
; (e) 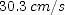 ]
]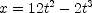 .
.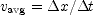 . Find the coordinate at the beginning and end of the interval and subtract the former from the latter to get
. Find the coordinate at the beginning and end of the interval and subtract the former from the latter to get 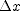 .
.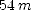 ; (b)
; (b) 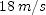 ; (c)
; (c) 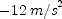 ; (d)
; (d) 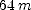 ; (e)
; (e) 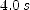 ; (f)
; (f) 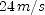 ; (g)
; (g) 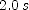 ; (h)
; (h) 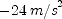 ; (i)
; (i) 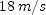 ]
]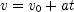 , where
, where  is the electron's velocity at any time
is the electron's velocity at any time 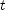 ,
, 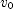 is its velocity at time
is its velocity at time 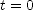 , and
, and  is its acceleration. Let
is its acceleration. Let 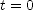 at the instant the electron's velocity is
at the instant the electron's velocity is 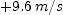 and evaluate the expression for (a)
and evaluate the expression for (a)  and for
and for  .
.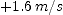 ; (b)
; (b) 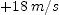 ]
]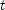 is given by
is given by  , where
, where 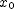 is its coordinate at
is its coordinate at 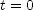 ,
, 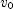 is its velocity then, and
is its velocity then, and  is its acceleration. According to the graph
is its acceleration. According to the graph 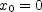 . The slope of the curve at
. The slope of the curve at  appears to be zero so you may take
appears to be zero so you may take 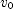 to be zero. Thus
to be zero. Thus 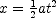 . The graph also shows that
. The graph also shows that 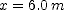 at
at  . Put this information into the equation and solve for
. Put this information into the equation and solve for  .
.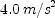 ; (b)
; (b)  ]
] axis at the position of train A when it starts slowing and suppose the train has velocity
axis at the position of train A when it starts slowing and suppose the train has velocity 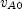 (
(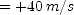 from the graph) at that time. Its velocity as a function of time is given by
from the graph) at that time. Its velocity as a function of time is given by 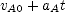 , where
, where 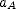 is its acceleration. This is the slope of the upper line on the graph and is negative. Solve for the time when train A stops and use
is its acceleration. This is the slope of the upper line on the graph and is negative. Solve for the time when train A stops and use  to find its position when it stops.
to find its position when it stops.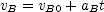 , where
, where  is its velocity at
is its velocity at 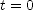 (
( from the graph), and
from the graph), and 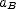 is its acceleration. This is the slope of the lower line on the graph and is positive. Solve for the time when train B stops and use
is its acceleration. This is the slope of the lower line on the graph and is positive. Solve for the time when train B stops and use  to find its position when it stops. Here
to find its position when it stops. Here 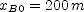 . The separation of the trains when both have stopped is the difference of the coordinates you have found.
. The separation of the trains when both have stopped is the difference of the coordinates you have found.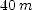 ]
] axis of a coordinate system so the origin is at the front end of the passenger train when it starts slowing and suppose the train is moving in the positive
axis of a coordinate system so the origin is at the front end of the passenger train when it starts slowing and suppose the train is moving in the positive  direction. The coordinate of the front end is then given by
direction. The coordinate of the front end is then given by 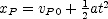 , where
, where 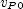 is its velocity at
is its velocity at 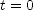 and
and  is its acceleration. Its velocity is given by
is its acceleration. Its velocity is given by 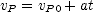 . The coordinate of the back end of the locomotive is given by
. The coordinate of the back end of the locomotive is given by  , where
, where 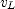 is its velocity.
is its velocity.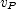 equal to the expression for
equal to the expression for 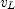 and the expression for
and the expression for 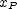 equal to the expression for
equal to the expression for 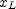 . Solve these equations simultaneously for
. Solve these equations simultaneously for  . (You can also solve for the time when these conditions are met but you are not asked for this.) Be sure to convert the given speeds to meters per second.
. (You can also solve for the time when these conditions are met but you are not asked for this.) Be sure to convert the given speeds to meters per second. ]
] , where
, where 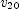 is the velocity with which it is thrown,
is the velocity with which it is thrown, 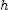 is the height of the bridge above the roadway, and
is the height of the bridge above the roadway, and 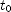 (
( ) is the time it is thrown. Here the origin is placed at the roadway and
) is the time it is thrown. Here the origin is placed at the roadway and 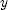 is taken to be positive in the upward direction. You need to know the value of
is taken to be positive in the upward direction. You need to know the value of 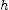 .
.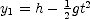 . Set
. Set 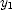 equal to zero and solve for
equal to zero and solve for 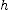 using
using 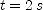 . Use this value and
. Use this value and 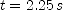 in the equation for
in the equation for 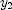 and solve for
and solve for 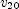 .
.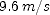 ]
]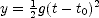 , where
, where 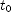 is the time the drop started. Suppose
is the time the drop started. Suppose 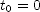 for the first drop,
for the first drop,  for the second,
for the second, 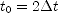 for the third, and
for the third, and  for the fourth. Each drop hits the floor when
for the fourth. Each drop hits the floor when 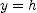 , the height of the nozzle above the floor. For the first drop
, the height of the nozzle above the floor. For the first drop  . Solve for
. Solve for 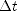 . The coordinate of the second drop at this time is
. The coordinate of the second drop at this time is 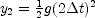 and the coordinate of the third drop is
and the coordinate of the third drop is  .
. ; (b)
; (b) 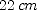 ]
]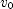 when falls past that point. If
when falls past that point. If 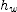 is the top-to-bottom dimension of the window, then
is the top-to-bottom dimension of the window, then 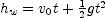 , where
, where 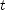 is the time to pass the window. Solve for
is the time to pass the window. Solve for  .
. . To find the length of the second segment solve for the distance the ball falls in
. To find the length of the second segment solve for the distance the ball falls in 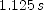 , starting with a downward velocity of
, starting with a downward velocity of 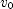 . The time here is the time for the ball to pass the window plus the time for it to fall from the bottom of the window to the sidewalk.
. The time here is the time for the ball to pass the window plus the time for it to fall from the bottom of the window to the sidewalk. ]
]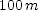 ]
] be the initial velocity and
be the initial velocity and 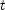 the time to reach the highest point. The velocity at the highest point is zero. Solve
the time to reach the highest point. The velocity at the highest point is zero. Solve 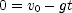 for
for 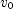 , then use
, then use  to compute the coordinate
to compute the coordinate 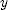 of the highest point, relative to the top of the building. Lastly, use the same equation, but with
of the highest point, relative to the top of the building. Lastly, use the same equation, but with 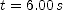 to compute the coordinate of the ground relative to the top of the building. The magnitude of the coordinate is the height of the building.
to compute the coordinate of the ground relative to the top of the building. The magnitude of the coordinate is the height of the building.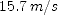 ; (b)
; (b) 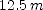 ; (c)
; (c) 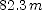 ]
] for the acceleration
for the acceleration  . Here
. Here  is the final velocity (0) and
is the final velocity (0) and 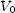 is the initial velocity (
is the initial velocity (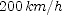 ). You need to convert this to meters per second. Solve
). You need to convert this to meters per second. Solve  for the time of braking
for the time of braking  . The distance traveled during the reaction time
. The distance traveled during the reaction time 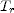 is
is  .
. ; (b)
; (b) 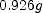 ; (c)
; (c) 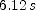 ; (d)
; (d) 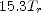 ; (e) braking; (f)
; (e) braking; (f) 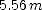 ]
] to compute the change in the coordinate. The average acceleration is the change in the velocity divided by the time for the change. Differentiate the expression for
to compute the change in the coordinate. The average acceleration is the change in the velocity divided by the time for the change. Differentiate the expression for  to obtain an expression for the velocity, then evaluate it for the two times. The instantaneous acceleration is the derivative of the velocity with respect to time.
to obtain an expression for the velocity, then evaluate it for the two times. The instantaneous acceleration is the derivative of the velocity with respect to time. ; (b)
; (b)  ; (c)
; (c)  ; (d)
; (d) 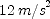 ; (e)
; (e) 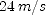 ; (f)
; (f) 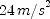 ]
]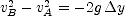 , where
, where 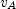 is the velocity of the stone when it is at A,
is the velocity of the stone when it is at A, 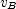 is its velocity when it is at B, and
is its velocity when it is at B, and 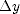 is the height of B above A. Put
is the height of B above A. Put 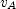 equal to
equal to  and
and 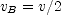 , then solve for
, then solve for  .
. 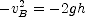 to compute the maximum height
to compute the maximum height  that the stone rises above point B.
that the stone rises above point B. ; (b)
; (b) 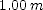 ]
]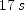 ; (b)
; (b) 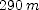 ]
] ; (b)
; (b) 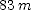 ]
]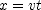 to find the distance traveled at each rate, then sum the distances to find the total distance. for part (b) use
to find the distance traveled at each rate, then sum the distances to find the total distance. for part (b) use 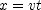 to find the time for each rate, then sum the times to find the total time.
to find the time for each rate, then sum the times to find the total time.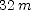 ; (b)
; (b) 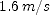 (c)
(c) 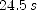 ; (d)
; (d) 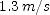 ]
]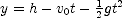 , with
, with 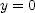 to find an expression for the time to reach the ground and
to find an expression for the time to reach the ground and 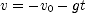 to find an expression for the velocity of the ball just before it hits the ground. Here
to find an expression for the velocity of the ball just before it hits the ground. Here  is a speed, not a velocity. For parts (c) and (d) use
is a speed, not a velocity. For parts (c) and (d) use 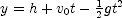 and
and 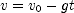 .
.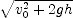 ; (b)
; (b) 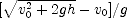 ; (c) same as (a); (d)
; (c) same as (a); (d) 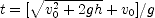 , greater]
, greater]