 | |  | Motion in Two and Three Dimensions
| | | |
|  |  | |  |  |  |  |
|
 |
| 4.1 | What is Physics? |
 |
 |
In this chapter we continue looking at the aspect of physics that analyzes motion, but now the motion can be in two or three dimensions. For example, medical researchers and aeronautical engineers might concentrate on the physics of the two- and three-dimensional turns taken by fighter pilots in dogfights because a modern high-performance jet can take a tight turn so quickly that the pilot immediately loses consciousness. A sports engineer might focus on the physics of basketball. For example, in a
free throw (where a player gets an uncontested shot at the basket from about 4.3 m), a player might employ the
overhand push shot, in which the ball is pushed away from about shoulder height and then released. Or the player might use an
underhand loop shot, in which the ball is brought upward from about the belt-line level and released. The first technique is the overwhelming choice among professional players, but the legendary Rick Barry set the record for free-throw shooting with the underhand technique.
Motion in three dimensions is not easy to understand. For example, you are probably good at driving a car along a freeway (one-dimensional motion) but would probably have a difficult time in landing an airplane on a runway (three-dimensional motion) without a lot of training.
In our study of two- and three-dimensional motion, we start with position and displacement.
| 4.2 | Position and Displacement |
 |
 |
One general way of locating a particle (or particle-like object) is with a
position vector 
, which is a vector that extends from a reference point (usually the origin) to the particle. In the unit-vector notation of Section 3-5,

can be written
 |
| (4-1) |
 |
where

,
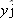
, and
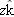
are the vector components of

and the coefficients
x,
y, and
z are its scalar components.
The coefficients
x,
y, and
z give the particle’s location along the coordinate axes and relative to the origin; that is, the particle has the rectangular coordinates (
x,
y,
z). For instance, Fig.
4-1 shows a particle with position vector
and rectangular coordinates (−3 m, 2 m, 5 m). Along the
x axis the particle is 3 m from the origin, in the
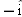
direction. Along the
y axis it is 2 m from the origin, in the
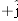
direction. Along the
z axis it is 5 m from the origin, in the
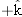
direction.
 |  | |  |  | FIGURE 4-1 | The position vector 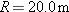 for a particle is the vector sum of its vector components. for a particle is the vector sum of its vector components.
|
|  |
|  |
As a particle moves, its position vector changes in such a way that the vector always extends to the particle from the reference point (the origin). If the position vector changes—say, from
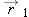
to
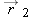
during a certain time interval—then the particle’s
displacement 
during that time interval is
 |
| (4-2) |
 |
Using the unit-vector notation of Eq.
4-1, we can rewrite this displacement as
or as
 |
| (4-3) |
 |
where coordinates (
x1,
y1,
z1) correspond to position vector
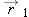
and coordinates (
x2,
y2,
z2) correspond to position vector
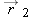
. We can also rewrite the displacement by substituting

for (
x2 −
x1),

for (
y2 −
y1), and

for (
z2 −
z1):
 |
 |  |  |
A rabbit runs across a parking lot on which a set of coordinate axes has, strangely enough, been drawn. The coordinates of the rabbit’s position as functions of time t (second) are given by
and
(a) At 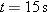 , what is the rabbit’s position vector  in unit-vector notation and in magnitude-angle notation?  . .
Calculations: We can write
(We write 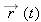 rather than  because the components are functions of t, and thus  is also.)
At 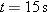 , the scalar components are
and
so
which is drawn in Fig. 4-3a. To get the magnitude and angle of  , we use Eq. 3-6:
and
 |  | |  |  | FIGURE 4-3 | (a) A rabbit’s position vector  at time at time  . The scalar components of . The scalar components of 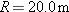 are shown along the axes. (b) The rabbit’s path and its position at five values of t. are shown along the axes. (b) The rabbit’s path and its position at five values of t.
|
|  |
|  |
Check: Although 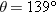 has the same tangent as −41°, the components of  indicates that the desired angle is 139° − 180° = −41°.
|  |  |
|  |  |  |  |
|
 |
 |
|
(b) Graph the rabbit’s path for t = 0 to t = 25 s.
Graphing: We can repeat part (a) for several values of t and then plot the results. Figure 4-3b shows the plots for five values of t and the path connecting them. We can also plot Eqs. 4-5 and 4-6 on a calculator.
|
 |
| 4.3 | Average Velocity and Instantaneous Velocity |
 |
 |
If a particle moves from one point to another, we might need to know how fast it moves. Just as in Chapter
2, we can define two quantities that deal with “how fast”:
average velocity and
instantaneous velocity. However, here we must consider these quantities as vectors and use vector notation.
If a particle moves through a displacement

in a time interval

, then its
average velocity 
is
or
 |
| (4-8) |
 |
This tells us that the direction of

(the vector on the left side of Eq.
4-8) must be the same as that of the displacement

(the vector on the right side). Using Eq.
4-4, we can write Eq.
4-8 in vector components as
For example, if the particle in Sample Problem
4-1 moves from its initial position to its later position in 2.0 s, then its average velocity during that move is
That is, the average velocity (a vector quantity) has a component of 6.0 m/s along the
x axis and a component of 1.5 m/s along the
z axis.
When we speak of the
velocity of a particle, we usually mean the particle’s
instantaneous velocity 
at some instant. This

is the value that

approaches in the limit as we shrink the time interval

to 0 about that instant. Using the language of calculus, we may write

as the derivative
 |
| (4-10) |
 |
To find the instantaneous velocity of the particle at, say, instant
t1 (when the particle is at position 1), we shrink interval

to 0 about
t1. Three things happen as we do so. (1) Position vector
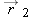
in Fig.
4-4 moves toward
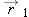
so that

shrinks toward zero. (2) The direction of
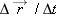
(and thus of

) approaches the direction of the line tangent to the particle’s path at position 1. (3) The average velocity

approaches the instantaneous velocity

at
t1.
In the limit as
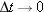
, we have
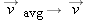
and, most important here,

takes on the direction of the tangent line. Thus,

has that direction as well:
The result is the same in three dimensions:

is always tangent to the particle’s path.
To write Eq.
4-10 in unit-vector form, we substitute for

from Eq.
4-1:
This equation can be simplified somewhat by writing it as
 |
| (4-11) |
 |
where the scalar components of

are
 |
| (4-12) |
 |
For example,
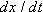
is the scalar component of

along the
x axis. Thus, we can find the scalar components of

by differentiating the scalar components of

.
Figure
4-5 shows a velocity vector

and its scalar
x and
y components. Note that

is tangent to the particle’s path at the particle’s position.
Caution: When a position vector is drawn, as in Figs.
4-1 through
4-4, it is an arrow that extends from one point (a “here”) to another point (a “there”). However, when a velocity vector is drawn, as in Fig.
4-5, it does
not extend from one point to another. Rather, it shows the instantaneous direction of travel of a particle at the tail, and its length (representing the velocity magnitude) can be drawn to any scale.
 |  | |  |  | FIGURE 4-5 | The velocity 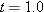 of a particle, along with the scalar components of of a particle, along with the scalar components of 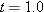 . .
|
|  |
|  |
 |
 |  |  |
For the rabbit in Sample Problem 4-2 find the velocity  at time 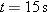 .  by taking derivatives of the components of the rabbit’s position vector. by taking derivatives of the components of the rabbit’s position vector.
Calculations: Applying the 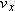 part of Eq. 4-12 to Eq. 4-5, we find the x component of  to be
At 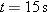 , this gives 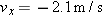 . Similarly, applying the  part of Eq. 4-12 to Eq. 4-6, we find
At 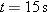 , this gives  . Equation 4-11 then yields
which is shown in Fig. 4-6, tangent to the rabbit’s path and in the direction the rabbit is running at 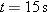 .  |  | |  |  | FIGURE 4-6 | The rabbit’s velocity 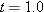 at at  . .
|
|  |
|  |
To get the magnitude and angle of  , either we use a vector-capable calculator or we follow Eq. 3-6 to write
and
Check: Is the angle −130° or −130° + 180° = 50°?.
|  |  |
|  |  |  |  |
|
 |
 |
| 4.4 | Average Acceleration and Instantaneous Acceleration |
 |
 |
When a particle’s velocity changes from
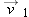
to
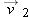
in a time interval

, its
average acceleration 
during

is
or
 |
| (4-15) |
 |
If we shrink

to zero about some instant, then in the limit

approaches the
instantaneous acceleration (or
acceleration)

at that instant; that is,
 |
| (4-16) |
 |
If the velocity changes in
either magnitude
or direction (or both), the particle must have an acceleration.
We can write Eq.
4-16 in unit-vector form by substituting Eq.
4-11 for

to obtain
We can rewrite this as
 |
| (4-17) |
 |
where the scalar components of

are
 |
| (4-18) |
 |
To find the scalar components of

, we differentiate the scalar components of

.
 |
 |  |  |
For the rabbit in Sample Problems 4-2 and 4-3, find the acceleration  at time 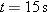 .  by taking derivatives of the rabbit’s velocity components. by taking derivatives of the rabbit’s velocity components.
Calculations: Applying the ax part of Eq. 4-18 to Eq. 4-13, we find the x component of  to be
Similarly, applying the ay part of Eq. 4-18 to Eq. 4-14 yields the y component as
We see that the acceleration does not vary with time (it is a constant) because the time variable t does not appear in the expression for either acceleration component. Equation 4-17 then yields
which is superimposed on the rabbit’s path in Fig. 4-8.  |  | |  |  | FIGURE 4-8 | The acceleration 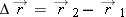 of the rabbit at of the rabbit at  . The rabbit happens to have this same acceleration at all points on its path. . The rabbit happens to have this same acceleration at all points on its path.
|
|  |
|  |
To get the magnitude and angle of  , either we use a vector-capable calculator or we follow Eq. 3-6. For the magnitude we have
For the angle we have
However, this angle, which is the one displayed on a calculator, indicates that  is directed to the right and downward in Fig. 4-8. Yet, we know from the components that  must be directed to the left and upward. To find the other angle that has the same tangent as −35° but is not displayed on a calculator, we add 180°:
This is consistent with the components of  . Note that  has the same magnitude and direction throughout the rabbit’s run because the acceleration is constant. |  |  |
|  |  |  |  |
|
 |
 |
 |
 |  |  |
A particle with velocity 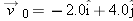 (in meters per second) at t = 0 undergoes a constant acceleration  of magnitude 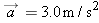 at an angle 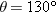 from the positive direction of the x axis. What is the particle’s velocity  at 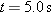 ? 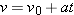 ) applies, we must apply it separately for motion parallel to the x axis and motion parallel to the y axis. ) applies, we must apply it separately for motion parallel to the x axis and motion parallel to the y axis.
Calculations: We find the velocity components 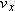 and  from the equations
In these equations, 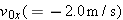 and 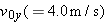 are the x and y components of 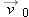 , and 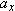 and 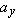 are the x and y components of  . To find 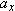 and 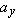 , we resolve  either with a vector-capable calculator or with Eq. 3-5:
When these values are inserted into the equations for 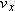 and  , we find that, at time 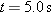 ,
Thus, at 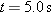 , we have, after rounding,
Either using a vector-capable calculator or following Eq. 3-6, we find that the magnitude and angle of  are
and
Check: Does 127° appear on your calculator’s display, or does −53° appear? Now sketch the vector  with its components to see which angle is reasonable.
|  |  |
|  |  |  |  |
|
 |
 |
| 4.5 | Projectile Motion |
 |
 |
Our goal here is to analyze projectile motion using the tools for two-dimensional motion described in Sections
4-2 through
4-4 and making the assumption that air has no effect on the projectile. Figure
4-10, which is analyzed in the next section, shows the path followed by a projectile when the air has no effect. The projectile is launched with an initial velocity
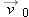
that can be written as
The components

and

can then be found if we know the angle

between
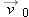
and the positive
x direction:
During its two-dimensional motion, the projectile’s position vector

and velocity vector

change continuously, but its acceleration vector

is constant and
always directed vertically downward. The projectile has
no horizontal acceleration.
 |  | |  |  | FIGURE 4-10 | The path of a projectile that is launched at 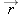 and and 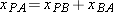 , with an initial velocity , with an initial velocity 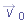 . The initial velocity and the velocities at various points along its path are shown, along with their components. Note that the horizontal velocity component remains constant but the vertical velocity component changes continuously. The range R is the horizontal distance the projectile has traveled when it returns to its launch height. . The initial velocity and the velocities at various points along its path are shown, along with their components. Note that the horizontal velocity component remains constant but the vertical velocity component changes continuously. The range R is the horizontal distance the projectile has traveled when it returns to its launch height.
|
|  |
|  |
Projectile motion, like that in Figs.
4-9 and
4-10, looks complicated, but we have the following simplifying feature (known from experiment):
This feature allows us to break up a problem involving two-dimensional motion into two separate and easier one-dimensional problems, one for the horizontal motion (with zero acceleration) and one for the vertical motion (with constant downward acceleration). Here are two experiments that show that the horizontal motion and the vertical motion are independent.
Two Golf Balls
A Great Student Rouser
If
g (the magnitude of the free-fall acceleration) were zero, the ball would follow the straight-line path shown in Fig.
4-12 and the can would float in place after the magnet released it. The ball would certainly hit the can.
However,
g is
not zero, but the ball
still hits the can! As Fig.
4-12 shows, during the time of flight of the ball, both ball and can fall the same distance
h from their zero-
g locations. The harder the demonstrator blows, the greater is the ball’s initial speed, the shorter the flight time, and the smaller the value of
h.
| 4.6 | Projectile Motion Analyzed |
 |
 |
Now we are ready to analyze projectile motion, horizontally and vertically.
The Horizontal Motion
Because there is
no acceleration in the horizontal direction, the horizontal component
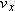
of the projectile’s velocity remains unchanged from its initial value

throughout the motion, as demonstrated in Fig.
4-13. At any time
t, the projectile’s horizontal displacement
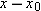
from an initial position
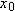
is given by Eq. 2-15 with
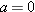
, which we write as
Because
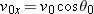
, this becomes
 |  | |  | | Source: Jamie Budge/Liaison/ Getty Images, Inc. |  |
 | FIGURE 4-13 | The vertical component of this skateboarder’s velocity is changing but not the horizontal component, which matches the skateboard’s velocity. As a result, the skateboard stays underneath him, allowing him to land on it.
|
|  |
|  |
The Vertical Motion
The vertical motion is the motion we discussed in Section 2-9 for a particle in free fall. Most important is that the acceleration is constant. Thus, the equations of Table 2-1 apply, provided we substitute −
g for
a and switch to
y notation. Then, for example, Eq. 2-15 becomes
where the initial vertical velocity component

is replaced with the equivalent
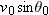
. Similarly, Eqs. 2-11 and 2-16 become
and
As is illustrated in Fig.
4-10 and Eq.
4-23, the vertical velocity component behaves just as for a ball thrown vertically upward. It is directed upward initially, and its magnitude steadily decreases to zero,
which marks the maximum height of the path. The vertical velocity component then reverses direction, and its magnitude becomes larger with time.
The Equation of the Path
We can find the equation of the projectile’s path (its
trajectory) by eliminating time
t between Eqs.
4-21 and
4-22. Solving Eq.
4-21 for
t and substituting into Eq.
4-22, we obtain, after a little rearrangement,
This is the equation of the path shown in Fig.
4-10. In deriving it, for simplicity we let
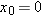
and

in Eqs.
4-21 and
4-22, respectively. Because
g,

, and

are constants, Eq.
4-25 is of the form

, in which
a and
b are constants. This is the equation of a parabola, so the path
is parabolic.
The Horizontal Range
The
horizontal range R of the projectile, as Fig.
4-10 shows, is the
horizontal distance the projectile has traveled when it returns to its initial (launch) height. To find range
R, let us put
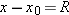
in Eq.
4-21 and
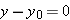
in Eq.
4-22, obtaining
and
Eliminating
t between these two equations yields
Using the identity

(see Appendix E), we obtain
Caution: This equation does
not give the horizontal distance traveled by a projectile when the final height is not the launch height.
Note that
R in Eq.
4-26 has its maximum value when
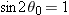
, which corresponds to
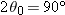
or

.
However, when the launch and landing heights differ, as in shot put, hammer throw, and basketball, a launch angle of 45° does not yield the maximum horizontal distance.
The Effects of the Air
We have assumed that the air through which the projectile moves has no effect on its motion. However, in many situations, the disagreement between our calculations and the actual motion of the projectile can be large because the air resists (opposes) the motion. Figure
4-14, for example, shows two paths for a fly ball that leaves the bat at an angle of 60° with the horizontal and an initial speed of 44.7 m/s. Path I (the baseball player’s fly ball) is a calculated path that approximates normal conditions of play, in air. Path II (the physics professor’s fly ball) is the path the ball would follow in a vacuum.
 |  | |  |  | FIGURE 4-14 | (I) The path of a fly ball calculated by taking air resistance into account. (II) The path the ball would follow in a vacuum, calculated by the methods of this chapter. See Table 4-1 for corresponding data. (Adapted from “The Trajectory of a Fly Ball,” by Peter J. Brancazio, The Physics Teacher, January 1985.)
|
|  |
|  |
 |  |
| | Path I (Air) | Path II (Vacuum) |
Range | 98.5 m | 177 m | Maximum height | 53.0 m | 76.8 m | Time of flight | 6.6 s | 7.9 s |
|
| |
|  |
|  |
 |
 |  | Sample Problem 4-6 Build your skill |  |
|  |  |  |
 |  |  |
(a) What should be the angle  of the pilot’s line of sight to the victim when the release is made?
Calculations: In Fig. 4-15, we see there that  is given by
where x is the horizontal coordinate of the victim (and of the capsule when it hits the water) and h = 500 m. We should be able to find x with Eq. 4-21:
Here we know that 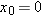 because the origin is placed at the point of release. Because the capsule is released and not shot from the plane, its initial velocity 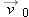 is equal to the plane’s velocity. Thus, we know also that the initial velocity has magnitude 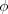 and angle 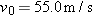 (measured relative to the positive direction of the x axis). However, we do not know the time t the capsule takes to move from the plane to the victim.
To find t, we next consider the vertical motion and specifically Eq. 4-22:
Here the vertical displacement 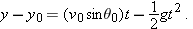 of the capsule is −500 m (the negative value indicates that the capsule moves downward). So,
Solving for t, we find 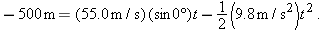 . Using that value in Eq. 4-28 yields
or
Then Eq. 4-27 gives us
|  |  |
|  |  |  |  |
|
 |
 |
(b) As the capsule reaches the water, what is its velocity  in unit-vector notation and in magnitude-angle notation? 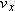 does not change from its initial value does not change from its initial value 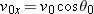 because there is no horizontal acceleration. (3) Component because there is no horizontal acceleration. (3) Component  changes from its initial value changes from its initial value 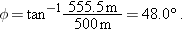 because there is a vertical acceleration. because there is a vertical acceleration.
Calculations: When the capsule reaches the water,
Using Eq. 4-23 and the capsule’s time of fall 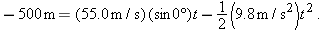 , we also find that when the capsule reaches the water,
Thus, at the water
Using Eq. 3-6 as a guide, we find that the magnitude and the angle of  are
|
 |
|
(b) What is the maximum range of the cannonballs?
Calculations: We have seen that maximum range corresponds to an elevation angle  of 45°. Thus,
As the pirate ship sails away, the two elevation angles at which the ship can be hit draw together, eventually merging at  when the ship is 690 m away. Beyond that distance the ship is safe.
|
 |
 |
 |  |  |
Suppose a baseball batter B hits a high fly ball to the outfield, directly toward an outfielder F and with a launch speed of  and a launch angle of  . During the flight, a line from the outfielder to the ball makes an angle 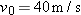 with the ground. Plot elevation angle 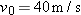 versus time t, assuming that the outfielder is already positioned to catch the ball, is 6.0 m too close to the batter, and is 6.0 m too far away.
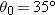 . .
Calculations: The ball can be caught if the outfielder’s distance from the batter is equal to the range R of the ball. Using Eq. 4-26, we find
Figure 4-17a shows a snapshot of the ball in flight when the ball is at height y and horizontal distance x from the batter (who is at the origin). The horizontal distance of the ball from the outfielder is  , and the elevation angle  of the ball in the outfielder’s view is given by  . For the height y, we use Eq. 4-22  , setting  . For the horizontal distance x, we substitute with Eq. 4-21 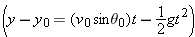 , setting 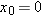 . Thus, using  and  , we have
 |  | |  |  | FIGURE 4-17 | The elevation angle  for a ball hit toward an outfielder is (a) defined and (b) plotted versus time t. for a ball hit toward an outfielder is (a) defined and (b) plotted versus time t.
|
|  |
|  |
Graphing this function versus t gives the middle plot in Fig. 4-17b. We see that the ball’s angle in the outfielder’s view increases at an almost steady rate throughout the flight.
If the outfielder is 6.0 m too close to the batter, we replace the distance of 153.42 m in Eq. 4-33 with 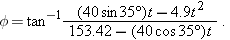 . Regraphing the function gives the “Too close” plot in Fig. 4-17b. Now the elevation angle of the ball rapidly increases toward the end of the flight as the ball soars over the outfielder’s head. If the outfielder is 6.0 m too far away from the batter, we replace the distance of 153.42 m in Eq. 4-33 with 159.42 m. The resulting plot is labeled “Too far” in the figure: The angle first increases and then rapidly decreases. Thus, if a ball is hit directly toward an outfield, the player can tell from the change in the ball’s elevation angle  whether to stay put, run toward the batter, or back away from the batter. |  |  |
|  |  |  |  |
|
 |
 |
 |
 |  | Sample Problem 4-9 Build your skill |  |
|  |  |  |
 |  |  |
At time  , a golf ball is shot from ground level into the air, as indicated in Fig. 4-18a. The angle  between the ball’s direction of travel and the positive direction of the x axis is given in Fig. 4-18b as a function of time t. The ball lands at 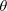 . What is the magnitude  of the ball’s launch velocity, at what height  above the launch level does the ball land, and what is the ball’s direction of travel just as it lands?  |  | |  |  | FIGURE 4-18 | (a) Path of a golf ball shot onto a plateau. (b) The angle  that gives the ball’s direction of motion during the flight is plotted versus time t. that gives the ball’s direction of motion during the flight is plotted versus time t.
|
|  |
|  |
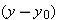 of the ball’s velocity does not change during the flight. (3) The vertical component of the ball’s velocity does not change during the flight. (3) The vertical component  of its velocity does change and is zero when the ball reaches maximum height. (4) The ball’s direction of travel at any time during the flight is at the angle of its velocity vector of its velocity does change and is zero when the ball reaches maximum height. (4) The ball’s direction of travel at any time during the flight is at the angle of its velocity vector  just then. That angle is given by tan just then. That angle is given by tan  , with the velocity components evaluated at that time. , with the velocity components evaluated at that time.
Calculations: When the ball reaches its maximum height, 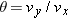 . So, the direction of the velocity  is horizontal, at angle 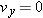 . From the graph, we see that this condition occurs at 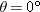 . We also see that the launch angle  (at t = 0) is 80°. Using Eq. 4-23 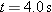 , with t = 4.0 s,  , 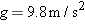 , and 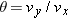 , we find
The ball lands at 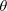 . Using Eq. 4-22  with  , we obtain
Just as the ball lands, its horizontal velocity 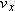 is still  ; substituting for  and  gives us 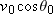 . We find its vertical velocity just then by using Eq. 4-23 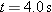 with 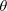 , which yields  . Thus, the angle of the ball’s direction of travel at landing is
|  |  |
|  |  |  |  |
|
 |
 |
| 4.7 | Uniform Circular Motion |
 |
 |
A particle is in uniform circular motion if it travels around a circle or a circular arc at constant (uniform) speed. Although the speed does not vary, the particle is accelerating because velocity changes in direction.
Figure
4-19 shows the relationship between the velocity and acceleration vectors at various stages during uniform circular motion. Both vectors have constant magnitude, but their directions change continuously. The velocity is always directed tangent to the circle in the direction of motion. The acceleration is always directed
radially inward. Because of this, the acceleration associated with uniform circular motion is called a
centripetal (meaning “center seeking”)
acceleration. As we prove next, the magnitude of this acceleration

is
 |
| (4-34) |
 |
where
r is the radius of the circle and
v is the speed of the particle.
 |  | |  |  | FIGURE 4-19 | Velocity and acceleration vectors for uniform circular motion.
|
|  |
|  |
In addition, during this acceleration at constant speed, the particle travels the circumference of the circle (a distance of

) in time
 |
| (4-35) |
 |
T is called the
period of revolution, or simply the
period, of the motion. It is, in general, the time for a particle to go around a closed path exactly once.
Proof of Eq. 4-34
To find the magnitude and direction of the acceleration for uniform circular motion, we consider Fig.
4-20. In Fig.
4-20a, particle
p moves at constant speed
v around a circle of radius
r. At the instant shown,
p has coordinates

and
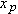
.
 |  | |  |  | FIGURE 4-20 | Particle p moves in counterclockwise uniform circular motion. (a) Its position and velocity  at a certain instant. (b) Velocity at a certain instant. (b) Velocity  . (c) Acceleration . (c) Acceleration  . .
|
|  |
|  |
Recall from Section
4-3 that the velocity

of a moving particle is always tangent to the particle’s path at the particle’s position. In Fig.
4-20a, that means

is perpendicular to a radius
r drawn to the particle’s position. Then the angle

that

makes with a vertical at
p equals the angle
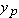
that radius
r makes with the
x axis.
The scalar components of

are shown in Fig.
4-20b. With them, we can write the velocity

as
Now, using the right triangle in Fig.
4-20a, we can replace
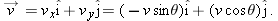
with
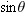
and
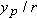
with
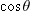
to write
To find the acceleration

of particle
p, we must take the time derivative of this equation. Noting that speed
v and radius
r do not change with time, we obtain
Now note that the rate
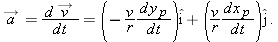
at which
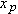
changes is equal to the velocity component

. Similarly,
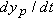
, and, again from Fig.
4-20b, we see that
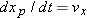
and
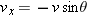
. Making these substitutions in Eq.
4-38, we find
This vector and its components are shown in Fig.
4-20c. Following Eq. 3-6, we find
as we wanted to prove. To orient

, we find the angle
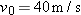
shown in Fig.
4-20c:
Thus,
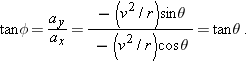
, which means that

is directed along the radius
r of Fig.
4-20a, toward the circle’s center, as we wanted to prove.
 |
 |  |  |
“Top gun” pilots have long worried about taking a turn too tightly. As a pilot’s body undergoes centripetal acceleration, with the head toward the center of curvature, the blood pressure in the brain decreases, leading to loss of brain function.
There are several warning signs. When the centripetal acceleration is 2g or 3g, the pilot feels heavy. At about 4g, the pilot’s vision switches to black and white and narrows to “tunnel vision.” If that acceleration is sustained or increased, vision ceases and, soon after, the pilot is unconscious—a condition known as g-LOC for “g-induced loss of consciousness.”
What is the magnitude of the acceleration, in g units, of a pilot whose aircraft enters a horizontal circular turn with a velocity of 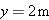 and 24.0 s later leaves the turn with a velocity of 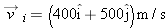 ?
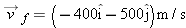 , where R is the circle’s radius. Also, the time required to complete a full circle is the period given by Eq. 4-35 , where R is the circle’s radius. Also, the time required to complete a full circle is the period given by Eq. 4-35 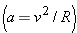 . .
Calculations: Because we do not know radius R, let’s solve Eq. 4-35 for R and substitute into Eq. 4-34. We find
Speed v here is the (constant) magnitude of the velocity during the turning. Let’s substitute the components of the initial velocity into Eq. 3-6:
To find the period T of the motion, first note that the final velocity is the reverse of the initial velocity. This means the aircraft leaves on the opposite side of the circle from the initial point and must have completed half a circle in the given 24.0 s. Thus a full circle would have taken 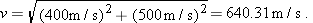 . Substituting these values into our equation for a, we find
|  |  |
|  |  |  |  |
|
 |
 |
| 4.8 | Relative Motion in One Dimension |
 |
 |
Suppose you see a duck flying north at 30 km/h.To another duck flying alongside, the first duck seems to be stationary. In other words, the velocity of a particle depends on the reference frame of whoever is observing or measuring the velocity. For our purposes, a reference frame is the physical object to which we attach our coordinate system. In everyday life, that object is the ground. For example, the speed listed on a speeding ticket is always measured relative to the ground. The speed relative to the police officer would be different if the officer were moving while making the speed measurement.
Suppose that Alex (at the origin of frame
A in Fig.
4-21) is parked by the side of a highway, watching car
P (the “particle”) speed past. Barbara (at the origin of frame
B) is driving along the highway at constant speed and is also watching car
P. Suppose that they both measure the position of the car at a given moment. From Fig.
4-21 we see that
The equation is read: “The coordinate

of
P as measured by
A is equal to the coordinate
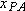
of
P as measured by
B plus the coordinate

of
B as measured by
A.” Note how this reading is supported by the sequence of the subscripts.
 |  | |  |  | FIGURE 4-21 | Alex (frame A) and Barbara (frame B) watch car P, as both B and P move at different velocities along the common x axis of the two frames. At the instant shown,  is the coordinate of B in the A frame. Also, P is at coordinate is the coordinate of B in the A frame. Also, P is at coordinate  in the B frame and coordinate in the B frame and coordinate 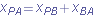 in the A frame. in the A frame.
|
|  |
|  |
Taking the time derivative of Eq.
4-40, we obtain
Thus, the velocity components are related by
 |
| (4-41) |
 |
This equation is read: “The velocity

of
P as measured by
A is equal to the velocity

of
P as measured by
B plus the velocity

of
B as measured by
A.” The term

is the velocity of frame
B relative to frame
A.
Here we consider only frames that move at constant velocity relative to each other. In our example, this means that Barbara (frame
B) drives always at constant velocity

relative to Alex (frame
A). Car
P (the moving particle), however, can change speed and direction (that is, it can accelerate).
To relate an acceleration of
P as measured by Barbara and by Alex, we take the time derivative of Eq.
4-41:
Because

is constant, the last term is zero and we have
 |
| (4-42) |
 |
In other words,
(b) If car P brakes to a stop relative to Alex (and thus relative to the ground) in time 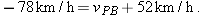 at constant acceleration, what is its acceleration 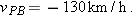 relative to Alex? 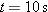 to relate the acceleration to the initial and final velocities of P. to relate the acceleration to the initial and final velocities of P.
Calculation: The initial velocity of P relative to Alex is 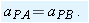 and the final velocity is 0. Thus,
|
 |
(c) What is the acceleration 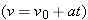 of car P relative to Barbara during the braking?
Calculation: We know the initial velocity of P relative to Barbara from part (a) 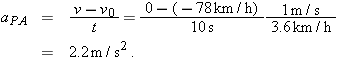 . The final velocity of P relative to Barbara is −52 km/h (this is the velocity of the stopped car relative to the moving Barbara). Thus,
Comment: We should have foreseen this result: Because Alex and Barbara have a constant relative velocity, they must measure the same acceleration for the car.
|
 |
| 4.9 | Relative Motion in Two Dimensions |
 |
 |
Our two observers are again watching a moving particle
P from the origins of reference frames
A and
B, while
B moves at a constant velocity
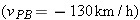
relative to
A. (The corresponding axes of these two frames remain parallel.) Figure
4-22 shows a certain instant during the motion. At that instant, the position vector of the origin of
B relative to the origin of
A is
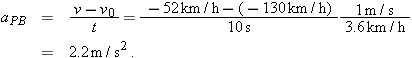
. Also, the position vectors of particle
P are

relative to the origin of
A and
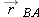
relative to the origin of
B. From the arrangement of heads and tails of those three position vectors, we can relate the vectors with
 |
| (4-43) |
 |
By taking the time derivative of this equation, we can relate the velocities
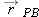
and
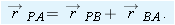
of particle
P relative to our observers:
 |
| (4-44) |
 |
By taking the time derivative of this relation, we can relate the accelerations

and
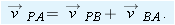
of the particle
P relative to our observers. However, note that because
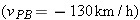
is constant, its time derivative is zero. Thus, we get
 |
| (4-45) |
 |
As for one-dimensional motion, we have the following rule: Observers on different frames of reference that move at constant velocity relative to each other will measure the
same acceleration for a moving particle.
 |  | |  |  | FIGURE 4-22 | Frame B has the constant two-dimensional velocity 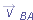 relative to frame A. The position vector of B relative to A is relative to frame A. The position vector of B relative to A is 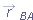 . The position vectors of particle P are . The position vectors of particle P are 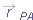 relative to A and relative to A and  relative to B. relative to B.
|
|  |
|  |
 |
 |  |  |
The situation is like the one in Fig. 4-22. Here the moving particle P is the plane, frame A is attached to the ground (call it G), and frame B is “attached” to the wind (call it W). We need a vector diagram like Fig. 4-22 but with the three velocity vectors.
Calculations: First we construct a sentence that relates the three vectors shown in Fig. 4-23b:
This relation is written in vector notation as
We need to resolve the vectors into components on the coordinate system of Fig. 4-23b and then solve Eq. 4-46 axis by axis. For the y components, we find
or
Solving for  gives us
Similarly, for the x components we find
Here, because 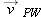 is parallel to the x axis, the component  is equal to the magnitude  . Substituting this notation and the value 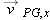 , we find
|  |  |
|  |  |  |  |
|
 |
 |
| 4.10 | Review & Summary |
 |
 |
Position Vector The location of a particle relative to the origin of a coordinate system is given by a
position vector 
, which in unit-vector notation is
Here

,
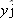
, and
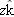
are the vector components of position vector

, and
x,
y, and
z are its scalar components (as well as the coordinates of the particle). A position vector is described either by a magnitude and one or two angles for orientation, or by its vector or scalar components.
Displacement If a particle moves so that its position vector changes from
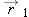
to
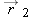
, the particle’s
displacement 
is
The displacement can also be written as
Average Velocity and Instantaneous Velocity If a particle undergoes a displacement

in time interval

, its
average velocity 
for that time interval is
As

in Eq.
4-8 is shrunk to 0,

reaches a limit called either the
velocity or the
instantaneous velocity 
:
which can be rewritten in unit-vector notation as
where
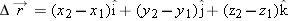
,
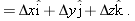
, and

. The instantaneous velocity

of a particle is always directed along the tangent to the particle’s path at the particle’s position.
Average Acceleration and Instantaneous Acceleration If a particle’s velocity changes from
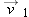
to
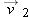
in time interval

, its
average acceleration during

is
As

in Eq.
4-15 is shrunk to 0,

reaches a limiting value called either the
acceleration or the
instantaneous acceleration 
:
In unit-vector notation,
where
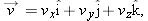
,

, and
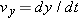
.
Projectile Motion Projectile motion is the motion of a particle that is launched with an initial velocity
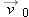
. During its flight, the particle’s horizontal acceleration is zero and its vertical acceleration is the free-fall acceleration −
g. (Upward is taken to be a positive direction.) If
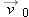
is expressed as a magnitude (the speed

) and an angle

(measured from the horizontal), the particle’s equations of motion along the horizontal
x axis and vertical
y axis are
The
trajectory (path) of a particle in projectile motion is parabolic and is given by
if
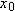
and
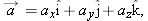
of Eqs.
4-21 to
4-24 are zero. The particle’s
horizontal range R, which is the horizontal distance from the launch point to the point at which the particle returns to the launch height, is
Uniform Circular Motion If a particle travels along a circle or circular arc of radius
r at constant speed
v, it is said to be in
uniform circular motion and has an acceleration

of constant magnitude
The direction of

is toward the center of the circle or circular arc, and

is said to be
centripetal. The time for the particle to complete a circle is
T is called the
period of revolution, or simply the
period, of the motion.
Relative Motion When two frames of reference
A and
B are moving relative to each other at constant velocity, the velocity of a particle
P as measured by an observer in frame
A usually differs from that measured from frame
B. The two measured velocities are related by
where
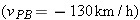
is the velocity of
B with respect to
A. Both observers measure the same acceleration for the particle:
 |
| 1. |
Figure 4-24 shows thes initial position i and the final position f of a particle. What are the (a) initial position vector 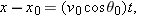 and (b) final position vector  , both in unit-vector notation? (c) What is the x component of displacement  ? |
 |
| 2. |
Figure 4-25 shows the path taken by a skunk foraging for trash food, from initial point i. The skunk took the same time T to go from each labeled point to the next along its path. Rank points a, b, and c according to the magnitude of the average velocity of the skunk to reach them from initial point i, greatest first. |
 |
| 3. |
You are to launch a rocket, from just above the ground, with one of the following initial velocity vectors: (1)  , (2) 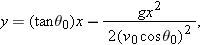 , (3)  , (4) 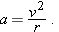 . In your coordinate system, x runs along level ground and y increases upward. (a) Rank the vectors according to the launch speed of the projectile, greatest first. (b) Rank the vectors according to the time of flight of the projectile, greatest first. |
 |
| 4. |
Figure 4-26 shows three situations in which identical projectiles are launched (at the same level) at identical initial speeds and angles. The projectiles do not land on the same terrain, however. Rank the situations according to the final speeds of the projectiles just before they land, greatest first. |
 |
| 5. |
When Paris was shelled from 100 km away with the WWI long-range artillery piece “Big Bertha,” the shells were fired at an angle greater than 45° to give them a greater range, possibly even twice as long as at 45°. Does that result mean that the air density at high altitudes increases with altitude or decreases?
|
 |
| 6. |
In Fig. 4-27, a cream tangerine is thrown up past windows 1, 2, and 3, which are identical in size and regularly spaced vertically. Rank those three windows according to (a) the time the cream tangerine takes to pass them and (b) the average speed of the cream tangerine during the passage, greatest first.
The cream tangerine then moves down past windows 4, 5, and 6, which are identical in size and irregularly spaced horizontally. Rank those three windows according to (c) the time the cream tangerine takes to pass them and (d) the average speed of the cream tangerine during the passage, greatest first.
|
 |
| 7. |
Figure 4-28 shows three paths for a football kicked from ground level. Ignoring the effects of air, rank the paths according to (a) time of flight, (b) initial vertical velocity component, (c) initial horizontal velocity component, and (d) initial speed, greatest first. |
 |
| 8. |
The only good use of a fruitcake is in catapult practice. Curve 1 in Fig. 4-29 gives the height y of a catapulted fruitcake versus the angle  between its velocity vector and its acceleration vector during flight. (a) Which of the lettered points on that curve corresponds to the landing of the fruitcake on the ground? (b) Curve 2 is a similar plot for the same launch speed but for a different launch angle. Does the fruitcake now land farther away or closer to the launch point? |
 |
| 9. |
An airplane flying horizontally at a constant speed of 350 km/h over level ground releases a bundle of food supplies. Ignore the effect of the air on the bundle. What are the bundle’s initial (a) vertical and (b) horizontal components of velocity? (c) What is its horizontal component of velocity just before hitting the ground? (d) If the airplane’s speed were, instead, 450 km/h, would the time of fall be longer, shorter, or the same?
|
 |
| 10. |
A ball is shot from ground level over level ground at a certain initial speed. Figure 4-30 gives the range R of the ball versus its launch angle 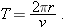 . Rank the three lettered points on the plot according to (a) the total flight time of the ball and (b) the ball’s speed at maximum height, greatest first. |
 |
| 11. |
In Fig. 4-31, particle P is in uniform circular motion, centered on the origin of an xy coordinate system. (a) At what values of  is the vertical component 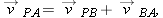 of the position vector greatest in magnitude? (b) At what values of  is the vertical component  of the particle’s velocity greatest in magnitude? (c) At what values of  is the vertical component 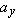 of the particle’s acceleration greatest in magnitude? |
 |
| 12. |
(a) Is it possible to be accelerating while traveling at constant speed? Is it possible to round a curve with (b) zero acceleration and (c) a constant magnitude of acceleration?
|
 |
| 13. |
Figure 4-32 shows four tracks (either half- or quarter-circles) that can be taken by a train, which moves at a constant speed. Rank the tracks according to the magnitude of a train’s acceleration on the curved portion, greatest first.
|
 |
|
 Tutoring problem available (at instructor's discretion) in WileyPLUS and WebAssign Tutoring problem available (at instructor's discretion) in WileyPLUS and WebAssign
SSM Worked-out solution available in Student Solutions Manual
ILW Interactive solution
• - ••• Number of dots indicates level of problem difficulty
 Additional information available in The Flying Circus of Physics Additional information available in The Flying Circus of Physics
|
|
| sec. 4-2 Position and Displacement |  |
|
| •1. |
A positron undergoes a displacement  , ending with the position vector  , in meters. What was the positron’s initial position vector? | |
| •2. |
A watermelon seed has the following coordinates:  ,  , and  . Find its position vector (a) in unit-vector notation and as (b) a magnitude and (c) an angle relative to the positive direction of the x axis. (d) Sketch the vector on a right-handed coordinate system. If the seed is moved to the xyz coordinates (3.00 m, 0 m, 0 m), what is its displacement (e) in unit-vector notation and as (f) a magnitude and (g) an angle relative to the positive x direction? | |
| •3. |
The position vector for an electron is  . (a) Find the magnitude of  . (b) Sketch the vector on a right-handed coordinate system. | |
| ••4. |
The minute hand of a wall clock measures 10 cm from its tip to the axis about which it rotates. The magnitude and angle of the displacement vector of the tip are to be determined for three time intervals. What are the (a) magnitude and (b) angle from a quarter after the hour to half past, the (c) magnitude and (d) angle for the next half hour, and the (e) magnitude and (f) angle for the hour after that?
| |
| sec. 4-3 Average Velocity and Instantaneous Velocity |  |
|
| •5. |
An ion’s position vector is initially  , and 10 s later it is  , all in meters. In unit-vector notation, what is its  during the 10 s? | |
| •6. |
An electron’s position is given by  , with t in seconds and  in meters. (a) In unit-vector notation, what is the electron’s velocity  ? At  , what is  (b) in unit-vector notation and as (c) a magnitude and (d) an angle relative to the positive direction of the x axis? | |
| •7. |
A train at a constant 60.0 km/h moves east for 40.0 min, then in a direction 50.0° east of due north for 20.0 min, and then west for 50.0 min. What are the (a) magnitude and (b) angle of its average velocity during this trip?
|  | |
| ••8. |
A plane flies 483 km east from city A to city B in 45.0 min and then 966 km south from city B to city C in 1.50 h. For the total trip, what are the (a) magnitude and (b) direction of the plane’s displacement, the (c) magnitude and (d) direction of its average velocity, and (e) its average speed?
| |
| ••9. |
Figure 4-33 gives the path of a squirrel moving about on level ground, from point A (at time  ), to points B (at  ), C (at  ), and finally D (at  ). Consider the average velocities of the squirrel from point A to each of the other three points. Of them, what are the (a) magnitude and (b) angle of the one with the least magnitude and the (c) magnitude and (d) angle of the one with the greatest magnitude? | |
| •••10. |
The position vector  locates a particle as a function of time t. Vector  is in meters, t is in seconds, and factors e and f are constants. Figure 4-34 gives the angle  of the particle’s direction of travel as a function of t (  is measured from the positive x direction). What are (a) e and (b) f, including units? | |
| sec. 4-4 Average Acceleration and Instantaneous Acceleration |  |
|
| •11. |
A particle moves so that its position (in meters) as a function of time (in seconds) is  . Write expressions for (a) its velocity and (b) its acceleration as functions of time. |  | |
| •12. |
A proton initially has  and then 4.0 s later has  (in meters per second). For that 4.0 s, what are (a) the proton’s average acceleration  in unit-vector notation, (b) the magnitude of  , and (c) the angle between  and the positive direction of the x axis? | |
| •13. |
The position  of a particle moving in an xy plane is given by  , with  in meters and t in seconds. In unit-vector notation, calculate (a)  , (b)  , and (c)  for  . (d) What is the angle between the positive direction of the x axis and a line tangent to the particle’s path at  ?  | |
| •14. |
At one instant a bicyclist is 40.0 m due east of a park’s flagpole, going due south with a speed of 10.0 m/s. Then 30.0 s later, the cyclist is 40.0 m due north of the flagpole, going due east with a speed of 10.0 m/s. For the cyclist in this 30.0 s interval, what are the (a) magnitude and (b) direction of the displacement, the (c) magnitude and (d) direction of the average velocity, and the (e) magnitude and (f) direction of the average acceleration?
| |
| ••15. |
A cart is propelled over an xy plane with acceleration components  and  . Its initial velocity has components  and  . In unit-vector notation, what is the velocity of the cart when it reaches its greatest y coordinate? | |
| ••16. |
A moderate wind accelerates a pebble over a horizontal xy plane with a constant acceleration  . At time  , the velocity is  . What are the (a) magnitude and (b) angle of its velocity when it has been displaced by 12.0 m parallel to the x axis? | |
| ••17. |
A particle leaves the origin with an initial velocity  and a constant acceleration  . When it reaches its maximum x coordinate, what are its (a) velocity and (b) position vector? |  | |
| ••18. |
The velocity  of a particle moving in the xy plane is given by  , with  in meters per second and t (> 0) in seconds. (a) What is the acceleration when  ? (b) When (if ever) is the acceleration zero? (c) When (if ever) is the velocity zero? (d) When (if ever) does the speed equal 10 m/s? | |
| •••19. |
The acceleration of a particle moving only on a horizontal xy plane is given by  , where  is in meters per second-squared and t is in seconds. At  , the position vector  locates the paticle, which then has the velocity vector  . At  , what are (a) its position vector in unit-vector notation and (b) the angle between its direction of travel and the positive direction of the x axis? | |
| •••20. |
In Fig. 4-35, particle A moves along the line  with a constant velocity  of magnitude 3.0 m/s and parallel to the x axis. At the instant particle A passes the y axis, particle B leaves the origin with zero initial speed and constant acceleration  of magnitude  . What angle  between  and the positive direction of the y axis would result in a collision? | |
| sec. 4-6 Projectile Motion Analyzed |  |
|
| •21. |
A projectile is fired horizontally from a gun that is 45.0 m above flat ground, emerging from the gun with a speed of 250 m/s. (a) How long does the projectile remain in the air? (b) At what horizontal distance from the firing point does it strike the ground? (c) What is the magnitude of the vertical component of its velocity as it strikes the ground?
| |
| •22. |
In the 1991 World Track and Field Championships in Tokyo, Mike Powell jumped 8.95 m, breaking by a full 5 cm the 23-year long-jump record set by Bob Beamon. Assume that Powell’s speed on takeoff was 9.5 m/s (about equal to that of a sprinter) and that  in Tokyo. How much less was Powell’s range than the maximum possible range for a particle launched at the same speed?
| |
| •23. |
The current world-record motorcycle jump is 77.0 m, set by Jason Renie. Assume that he left the take-off ramp at 12.0° to the horizontal and that the take-off and landing heights are the same. Neglecting air drag, determine his take-off speed.
| |
| •24. |
A small ball rolls horizontally off the edge of a tabletop that is 1.20 m high. It strikes the floor at a point 1.52 m horizontally from the table edge. (a) How long is the ball in the air? (b) What is its speed at the instant it leaves the table?
| |
| •25. |
A dart is thrown horizontally with an initial speed of 10 m/s toward point P, the bull’s-eye on a dart board. It hits at point Q on the rim, vertically below P, 0.19 s later. (a) What is the distance PQ? (b) How far away from the dart board is the dart released?
| |
| •26. |
In Fig. 4-36, a stone is projected at a cliff of height h with an initial speed of 42.0 m/s directed at angle  above the horizontal. The stone strikes at A, 5.50 s after launching. Find (a) the height h of the cliff, (b) the speed of the stone just before impact at A, and (c) the maximum height H reached above the ground. | |
| •27. |
A certain airplane has a speed of 290.0 km/h and is diving at an angle of  below the horizontal when the pilot releases a radar decoy (Fig. 4-37).The horizontal distance between the release point and the point where the decoy strikes the ground  . (a) How long is the decoy in the air? (b) How high was the release point? |  | |
| •28. |
A stone is catapulted at time  , with an initial velocity of magnitude 20.0 m/s and at an angle of 40.0° above the horizontal. What are the magnitudes of the (a) horizontal and (b) vertical components of its displacement from the catapult site at  ? Repeat for the (c) horizontal and (d) vertical components at  , and for the (e) horizontal and (f) vertical components at  . | |
| ••29. |
A lowly high diver pushes off horizontally with a speed of 2.00 m/s from the platform edge 10.0 m above the surface of the water. (a) At what horizontal distance from the edge is the diver 0.800 s after pushing off? (b) At what vertical distance above the surface of the water is the diver just then? (c) At what horizontal distance from the edge does the diver strike the water?
|  | |
| ••30. |
A trebuchet was a hurling machine built to attack the walls of a castle under siege. A large stone could be hurled against a wall to break apart the wall. The machine was not placed near the wall because then arrows could reach it from the castle wall. Instead, it was positioned so that the stone hit the wall during the second half of its flight. Suppose a stone is launched with a speed of  and at an angle of  . What is the speed of the stone if it hits the wall (a) just as it reaches the top of its parabolic path and (b) when it has descended to half that height? (c) As a percentage, how much faster is it moving in part (b) than in part (a)?
| |
| ••31. |
A plane, diving with constant speed at an angle of 53.0° with the vertical, releases a projectile at an altitude of 730 m. The projectile hits the ground 5.00 s after release. (a) What is the speed of the plane? (b) How far does the projectile travel horizontally during its flight? What are the (c) horizontal and (d) vertical components of its velocity just before striking the ground?
|  | |
| ••32. |
During a tennis match, a player serves the ball at 23.6 m/s, with the center of the ball leaving the racquet horizontally 2.37 m above the court surface. The net is 12 m away and 0.90 m high. When the ball reaches the net, (a) does the ball clear it and (b) what is the distance between the center of the ball and the top of the net? Suppose that, instead, the ball is served as before but now it leaves the racquet at 5.00° below the horizontal. When the ball reaches the net, (c) does the ball clear it and (d) what now is the distance between the center of the ball and the top of the net?
| |
| ••33. |
In a jump spike, a volleyball player slams the ball from overhead and toward the opposite floor. Controlling the angle of the spike is difficult. Suppose a ball is spiked from a height of 2.30 m with an initial speed of 20.0 m/s at a downward angle of 18.00°. How much farther on the opposite floor would it have landed if the downward angle were, instead, 8.00°?
| |
| ••34. |
A soccer ball is kicked from the ground with an initial speed of 19.5 m/s at an upward angle of 45°. A player 55 m away in the direction of the kick starts running to meet the ball at that instant. What must be his average speed if he is to meet the ball just before it hits the ground?
| |
| ••35. |
A projectile’s launch speed is five times its speed at maximum height. Find launch angle  . | |
| ••36. |
Suppose that a shot putter can put a shot at the world-class speed  and at a height of 2.160 m. What horizontal distance would the shot travel if the launch angle  is (a) 45.00° and (b) 42.00°? The answers indicate that the angle of 45°, which maximizes the range of projectile motion, does not maximize the horizontal distance when the launch and landing are at different heights.
| |
| ••37. |
A ball is shot from the ground into the air. At a height of 9.1 m, its velocity is  , with  horizontal and  upward. (a) To what maximum height does the ball rise? (b) What total horizontal distance does the ball travel? What are the (c) magnitude and (d) angle (below the horizontal) of the ball’s velocity just before it hits the ground? |  | |
| ••38. |
You throw a ball toward a wall at speed 25.0 m/s and at angle  above the horizontal (Fig. 4-38). The wall is distance  from the release point of the ball. (a) How far above the release point does the ball hit the wall? What are the (b) horizontal and (c) vertical components of its velocity as it hits the wall? (d) When it hits, has it passed the highest point on its trajectory? | |
| ••39. |
A rifle that shoots bullets at 460 m/s is to be aimed at a target 45.7 m away. If the center of the target is level with the rifle, how high above the target must the rifle barrel be pointed so that the bullet hits dead center?
|  | |
| ••40. |
A baseball leaves a pitcher’s hand horizontally at a speed of 161 km/h. The distance to the batter is 18.3 m. (a) How long does the ball take to travel the first half of that distance? (b) The second half? (c) How far does the ball fall freely during the first half? (d) During the second half? (e) Why aren’t the quantities in (c) and (d) equal?
| |
| ••41. |
In Fig. 4-39, a ball is thrown leftward from the left edge of the roof, at height h above the ground. The ball hits the ground 1.50 s later, at distance  from the building and at angle  with the horizontal. (a) Find h ( Hint: One way is to reverse the motion, as if on videotape.) What are the (b) magnitude and (c) angle relative to the horizontal of the velocity at which the ball is thrown? (d) Is the angle above or below the horizontal? | |
| ••42. |
A golf ball is struck at ground level. The speed of the golf ball as a function of the time is shown in Fig. 4-40, where  at the instant the ball is struck. (a) How far does the golf ball travel horizontally before returning to ground level? (b) What is the maximum height above ground level attained by the ball? | |
| ••43. |
In Fig. 4-41, a ball is launched with a velocity of magnitude 10.0 m/s, at an angle of 50.0° to the horizontal. The launch point is at the base of a ramp of horizontal length  and height  . A plateau is located at the top of the ramp. (a) Does the ball land on the ramp or the plateau? When it lands, what are the (b) magnitude and (c) angle of its displacement from the launch point? | |
| ••44. |
In 1939 or 1940, Emanuel Zacchini took his human-cannonball act to an extreme: After being shot from a cannon, he soared over three Ferris wheels and into a net (Fig. 4-42). (a) Treating him as a particle, calculate his clearance over the first wheel. (b) If he reached maximum height over the middle wheel, by how much did he clear it? (c) How far from the cannon should the net’s center have been positioned (neglect air drag)?
| |
| ••45. |
Upon spotting an insect on a twig overhanging water, an archer fish squirts water drops at the insect to knock it into the water (Fig. 4-43). Although the fish sees the insect along a straight-line path at angle  and distance d, a drop must be launched at a different angle  if its parabolic path is to intersect the insect. If  ,  , and the launch speed is 3.56 m/s, what  is required for the drop to be at the top of the parabolic path when it reaches the insect?
| |
| ••46. |
In Fig. 4-44, a ball is thrown up onto a roof, landing 4.00 s later at height  above the release level. The ball’s path just before landing is angled at  with the roof. (a) Find the horizontal distance d it travels. (See the hint to Problem 41.) What are the (b) magnitude and (c) angle (relative to the horizontal) of the ball’s initial velocity? | |
| ••47. |
A batter hits a pitched ball when the center of the ball is 1.22 m above the ground. The ball leaves the bat at an angle of 45° with the ground. With that launch, the ball should have a horizontal range (returning to the launch level) of 107 m. (a) Does the ball clear a 7.32-m-high fence that is 97.5 m horizontally from the launch point? (b) At the fence, what is the distance between the fence top and the ball center?
|  | |
| ••48. |
In basketball, hang is an illusion in which a player seems to weaken the gravitational acceleration while in midair. The illusion depends much on a skilled player’s ability to rapidly shift the ball between hands during the flight, but it might also be supported by the longer horizontal distance the player travels in the upper part of the jump than in the lower part. If a player jumps with an initial speed of  at an angle of  , what percent of the jump’s range does the player spend in the upper half of the jump (between maximum height and half maximum height)?
| |
| •••49. |
A skilled skier knows to jump upward before reaching a downward slope. Consider a jump in which the launch speed is  , the launch angle is  , the initial course is approximately flat, and the steeper track has a slope of 11.3°. Figure 4-45a shows a prejump that allows the skier to land on the top portion of the steeper track. Figure 4-45b shows a jump at the edge of the steeper track. In Fig. 4-45a, the skier lands at approximately the launch level, (a) In the landing, what is the angle  between the skier’s path and the slope? In Fig. 4-45b, (b) how far below the launch level does the skier land and (c) what is  ? (The greater fall and greater  can result in loss of control in the landing.)
| |
| •••50. |
A ball is to be shot from level ground toward a wall at distance x (Fig. 4-46a). Figure 4-46b shows the y component  of the ball’s velocity just as it would reach the wall, as a function of that distance x. What is the launch angle? | |
| •••51. |
A football kicker can give the ball an initial speed of 25 m/s. What are the (a) least and (b) greatest elevation angles at which he can kick the ball to score a field goal from a point 50 m in front of goalposts whose horizontal bar is 3.44 m above the ground?
|  | |
| •••52. |
A ball is to be shot from level ground with a certain speed. Figure 4-47 shows the range R it will have versus the launch angle  . The value of  determines the flight time; let  represent the maximum flight time. What is the least speed the ball will have during its flight if  is chosen such that the flight time is  ? | |
| •••53. |
A ball rolls horizontally off the top of a stairway with a speed of 1.52 m/s. The steps are 20.3 cm high and 20.3 cm wide. Which step does the ball hit first?
|  | |
| •••54. |
Two seconds after being projected from ground level, a projectile is displaced 40 m horizontally and 53 m vertically above its launch point. What are the (a) horizontal and (b) vertical components of the initial velocity of the projectile? (c) At the instant the projectile achieves its maximum height above ground level, how far is it displaced horizontally from the launch point?  | |
| •••55. |
In Fig. 4-48, a baseball is hit at a height  and then caught at the same height. It travels alongside a wall, moving up past the top of the wall 1.00 s after it is hit and then down past the top of the wall 4.00 s later, at distance  farther along the wall. (a) What horizontal distance is traveled by the ball from hit to catch? What are the (b) magnitude and (c) angle (relative to the horizontal) of the ball’s velocity just after being hit? (d) How high is the wall? | |
| sec. 4-7 Uniform Circular Motion |  |
|
| •56. |
A centripetal-acceleration addict rides in uniform circular motion with period 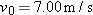 and radius  . At  his acceleration is  . At that instant, what are the values of (a)  and (b)  ? | |
| •57. |
A woman rides a carnival Ferris wheel at radius 15 m, completing five turns about its horizontal axis every minute. What are (a) the period of the motion, the (b) magnitude and (c) direction of her centripetal acceleration at the highest point, and the (d) magnitude and (e) direction of her centripetal acceleration at the lowest point?
|  | |
| •58. |
What is the magnitude of the acceleration of a sprinter running at 10 m/s when rounding a turn of a radius 25 m?
| |
| •59. |
When a large star becomes a supernova, its core may be compressed so tightly that it becomes a neutron star, with a radius of about 20 km (about the size of the San Francisco area). If a neutron star rotates once every second, (a) what is the speed of a particle on the star’s equator and (b) what is the magnitude of the particle’s centripetal acceleration? (c) If the neutron star rotates faster, do the answers to (a) and (b) increase, decrease, or remain the same?
| |
| •60. |
An Earth satellite moves in a circular orbit 640 km above Earth’s surface with a period of 98.0 min. What are the (a) speed and (b) magnitude of the centripetal acceleration of the satellite?
| |
| •61. |
A carnival merry-go-round rotates about a vertical axis at a constant rate. A man standing on the edge has a constant speed of 3.66 m/s and a centripetal acceleration  of magnitude  . Position vector  locates him relative to the rotation axis. (a) What is the magnitude of  ? What is the direction of  when  is directed (b) due east and (c) due south? | |
| •62. |
A rotating fan completes 1200 revolutions every minute. Consider the tip of a blade, at a radius of 0.15 m. (a) Through what distance does the tip move in one revolution? What are (b) the tip’s speed and (c) the magnitude of its acceleration? (d) What is the period of the motion?
| |
| ••63. |
A purse at radius 2.00 m and a wallet at radius 3.00 m travel in uniform circular motion on the floor of a merry-go-round as the ride turns. They are on the same radial line. At one instant, the acceleration of the purse is  . At that instant and in unit-vector notation, what is the acceleration of the wallet? | |
| ••64. |
A particle moves along a circular path over a horizontal xy coordinate system, at constant speed. At time  , it is at point (5.00 m, 6.00 m) with velocity  and acceleration in the positive x direction. At time  , it has velocity  and acceleration in the positive y direction. What are the (a) x and (b) y coordinates of the center of the circular path if  is less than one period? | |
| ••65. |
At  , the acceleration of a particle in counterclockwise circular motion is  . It moves at constant speed. At time  , its acceleration is  . What is the radius of the path taken by the particle if  is less than one period?  | |
| ••66. |
A particle moves horizontally in uniform circular motion, over a horizontal xy plane. At one instant, it moves through the point at coordinates (4.00 m, 4.00 m) with a velocity of  and an acceleration of  . What are the (a) x and (b) y coordinates of the center of the circular path? | |
| •••67. |
A boy whirls a stone in a horizontal circle of radius 1.5 m and at height 2.0 m above level ground. The string breaks, and the stone flies off horizontally and strikes the ground after traveling a horizontal distance of 10 m. What is the magnitude of the centripetal acceleration of the stone during the circular motion?
|  | |
| •••68. |
A cat rides a merry-go-round turning with uniform circular motion. At time  , the cat’s velocity is  , measured on a horizontal xy coordinate system. At  , its velocity is  . What are (a) the magnitude of the cat’s centripetal acceleration and (b) the cat’s average acceleration during the time interval  , which is less than one period? | |
| sec. 4-8 Relative Motion in One Dimension |  |
|
| •69. |
A cameraman on a pickup truck is traveling westward at 20 km/h while he videotapes a cheetah that is moving westward 30 km/h faster than the truck. Suddenly, the cheetah stops, turns, and then runs at 45 km/h eastward, as measured by a suddenly nervous crew member who stands alongside the cheetah’s path. The change in the animal’s velocity takes 2.0 s. What are the (a) magnitude and (b) direction of the animal’s acceleration according to the cameraman and the (c) magnitude and (d) direction according to the nervous crew member?
| |
| •70. |
A boat is traveling upstream in the positive direction of an x axis at 14 km/h with respect to the water of a river. The water is flowing at 9.0 km/h with respect to the ground. What are the (a) magnitude and (b) direction of the boat’s velocity with respect to the ground? A child on the boat walks from front to rear at 6.0 km/h with respect to the boat. What are the (c) magnitude and (d) direction of the child’s velocity with respect to the ground?
| |
| ••71. |
A suspicious-looking man runs as fast as he can along a moving sidewalk from one end to the other, taking 2.50 s. Then security agents appear, and the man runs as fast as he can back along the sidewalk to his starting point, taking 10.0 s. What is the ratio of the man’s running speed to the sidewalk’s speed?
| |
| sec. 4-9 Relative Motion in Two Dimensions |  |
|
| •72. |
A rugby player runs with the ball directly toward his opponent’s goal, along the positive direction of an x axis. He can legally pass the ball to a teammate as long as the ball’s velocity relative to the field does not have a positive x component. Suppose the player runs at speed 4.0 m/s relative to the field while he passes the ball with velocity  relative to himself. If  has magnitude 6.0 m/s, what is the smallest angle it can have for the pass to be legal? | |
| ••73. |
Two ships, A and B, leave port at the same time. Ship A travels northwest at 24 knots, and ship B travels at 28 knots in a direction 40° west of south. (1 knot = 1 nautical mile per hour; see Appendix D.) What are the (a) magnitude and (b) direction of the velocity of ship A relative to B? (c) After what time will the ships be 160 nautical miles apart? (d) What will be the bearing of B (the direction of B’s position) relative to A at that time?
|  | |
| ••74. |
A light plane attains an airspeed of 500 km/h.The pilot sets out for a destination 800 km due north but discovers that the plane must be headed 20.0° east of due north to fly there directly. The plane arrives in 2.00 h. What were the (a) magnitude and (b) direction of the wind velocity?
| |
| ••75. |
Snow is falling vertically at a constant speed of 8.0 m/s. At what angle from the vertical do the snowflakes appear to be falling as viewed by the driver of a car traveling on a straight, level road with a speed of 50 km/h?
|  | |
| ••76. |
After flying for 15 min in a wind blowing 42 km/h at an angle of 20° south of east, an airplane pilot is over a town that is 55 km due north of the starting point. What is the speed of the airplane relative to the air?
| |
| ••77. |
A train travels due south at 30 m/s (relative to the ground) in a rain that is blown toward the south by the wind. The path of each raindrop makes an angle of 70° with the vertical, as measured by an observer stationary on the ground. An observer on the train, however, sees the drops fall perfectly vertically. Determine the speed of the raindrops relative to the ground.
|  | |
| ••78. |
A 200-m-wide river flows due east at a uniform speed of 2.0 m/s. A boat with a speed of 8.0 m/s relative to the water leaves the south bank pointed in a direction 30° west of north. What are the (a) magnitude and (b) direction of the boat’s velocity relative to the ground? (c) How long does the boat take to cross the river?  | |
| ••79. |
Two highways intersect as shown in Fig. 4-49. At the instant shown, a police car P is distance  from the intersection and moving at speed  . Motorist M is distance  from the intersection and moving at speed  . (a) In unit-vector notation, what is the velocity of the motorist with respect to the police car? (b) For the instant shown in Fig. 4-49, what is the angle between the velocity found in (a) and the line of sight between the two cars? (c) If the cars maintain their velocities, do the answers to (a) and (b) change as the cars move nearer the intersection? | |
| ••80. |
In the overhead view of Fig. 4-50, Jeeps P and B race along straight lines, across flat terrain, and past stationary border guard A. Relative to the guard, B travels at a constant speed of 20.0 m/s, at the angle  . Relative to the guard, P has accelerated from rest at a constant rate of  at the angle  . At a certain time during the acceleration, P has a speed of 40.0 m/s. At that time, what are the (a) magnitude and (b) direction of the velocity of P relative to B and the (c) magnitude and (d) direction of the acceleration of P relative to B? | |
| •••81. |
Ship A is located 4.0 km north and 2.5 km east of ship B. Ship A has a velocity of 22 km/h toward the south, and ship B has a velocity of 40 km/h in a direction 37° north of east. (a) What is the velocity of A relative to B in unit-vector notation with  toward the east? (b) Write an expression (in terms of  and  ) for the position of A relative to B as a function of t, where  when the ships are in the positions described above. (c) At what time is the separation between the ships least? (d) What is that least separation? | |
| •••82. |
A 200-m-wide river has a uniform flow speed of 1.1 m/s through a jungle and toward the east. An explorer wishes to leave a small clearing on the south bank and cross the river in a powerboat that moves at a constant speed of 4.0 m/s with respect to the water. There is a clearing on the north bank 82 m upstream from a point directly opposite the clearing on the south bank. (a) In what direction must the boat be pointed in order to travel in a straight line and land in the clearing on the north bank? (b) How long will the boat take to cross the river and land in the clearing?
| |
Additional Problems
| 83. |
You are kidnapped by political-science majors (who are upset because you told them political science is not a real science). Although blindfolded, you can tell the speed of their car (by the whine of the engine), the time of travel (by mentally counting off seconds), and the direction of travel (by turns along the rectangular street system). From these clues, you know that you are taken along the following course: 50 km/h for 2.0 min, turn 90° to the right, 20 km/h for 4.0 min, turn 90° to the right, 20 km/h for 60 s, turn 90° to the left, 50 km/h for 60 s, turn 90° to the right, 20 km/h for 2.0 min, turn 90° to the left, 50 km/h for 30 s. At that point, (a) how far are you from your starting point, and (b) in what direction relative to your initial direction of travel are you?
| |
| 84. |
Curtain of death. A large metallic asteroid strikes Earth and quickly digs a crater into the rocky material below ground level by launching rocks upward and outward. The following table gives five pairs of launch speeds and angles (from the horizontal) for such rocks, based on a model of crater formation. (Other rocks, with intermediate speeds and angles, are also launched.) Suppose that you are at  when the asteroid strikes the ground at time  and position  (Fig. 4-51). (a) At  , what are the x and y coordinates of the rocks headed in your direction from launches A through E? (b) Plot these coordinates and then sketch a curve through the points to include rocks with intermediate launch speeds and angles. The curve should indicate what you would see as you look up into the approaching rocks and what dinosaurs must have seen during asteroid strikes long ago.
 |  |
Launch | Speed (m/s) | Angle (degrees) | A | 520 | 14.0 | B | 630 | 16.0 | C | 750 | 18.0 | D | 870 | 20.0 | E | 1000 | 22.0 |
|
| |
|  |
|  |
| |
| 85. |
In Fig. 4-52, a lump of wet putty moves in uniform circular motion as it rides at a radius of 20.0 cm on the rim of a wheel rotating counterclock wise with a period of 5.00 ms. The lump then happens to fly off the rim at the 5 o’clock position (as if on a clock face). It leaves the rim at a height of  from the floor and at a distance  from a wall. At what height on the wall does the lump hit? | |
| 86. |
A particle is in uniform circular motion about the origin of an xy coordinate system, moving clockwise with a period of 7.00 s. At one instant, its position vector (from the origin) is  . At that instant, what is its velocity in unit-vector notation? | |
| 87. |
In Fig. 4-53, a ball is shot directly upward from the ground with an initial speed of  . Simultaneously, a construction elevator cab begins to move upward from the ground with a constant speed of  . What maximum height does the ball reach relative to (a) the ground and (b) the cab floor? At what rate does the speed of the ball change relative to (c) the ground and (d) the cab floor? | |
| 88. |
In Fig. 4-54a, a sled moves in the negative x direction at constant speed  while a ball of ice is shot from the sled with a velocity  relative to the sled. When the ball lands, its horizontal displacement  relative to the ground (from its launch position to its landing position) is measured. Figure 4-54b gives  as a function of  . Assume the ball lands at approximately its launch height. What are the values of (a)  and (b)  ? The ball’s displacement  relative to the sled can also be measured. Assume that the sled’s velocity is not changed when the ball is shot. What is  when  is (c) 5.0 m/s and (d) 15 m/s? | |
| 89. |
A woman who can row a boat at 6.4 km/h in still water faces a long, straight river with a width of 6.4 km and a current of 3.2 km/h. Let  point directly across the river and  point directly downstream. If she rows in a straight line to a point directly opposite her starting position, (a) at what angle to  must she point the boat and (b) how long will she take? (c) How long will she take if, instead, she rows 3.2 km down the river and then back to her starting point? (d) How long if she rows 3.2 km up the river and then back to her starting point? (e) At what angle to  should she point the boat if she wants to cross the river in the shortest possible time? (f) How long is that shortest time? | |
| 90. |
In Fig. 4-55, a radar station detects an airplane approach ing directly from the east. At first observation, the airplane is at distance  from the station and at angle  above the horizon. The airplane is tracked through an angular change  in the vertical east–west plane; its distance is then  . Find the (a) magnitude and (b) direction of the airplane’s displacement during this period. | |
| 91. |
A rifle is aimed horizontally at a target 30 m away. The bullet hits the target 1.9 cm below the aiming point. What are (a) the bullet’s time of flight and (b) its speed as it emerges from the rifle?
|  | |
| 92. |
The fast French train known as the TGV (Train à Grande Vitesse) has a scheduled average speed of 216 km/h. (a) If the train goes around a curve at that speed and the magnitude of the acceleration experienced by the passengers is to be limited to 0.050g, what is the smallest radius of curvature for the track that can be tolerated? (b) At what speed must the train go around a curve with a 1.00 km radius to be at the acceleration limit?
| |
| 93. |
A magnetic field can force a charged particle to move in a circular path. Suppose that an electron moving in a circle experiences a radial acceleration of magnitude  in a particular magnetic field. (a) What is the speed of the electron if the radius of its circular path is 15 cm? (b) What is the period of the motion? | |
| 94. |
The position vector for a proton is initially  and then later is  , all in meters. (a) What is the proton’s displacement vector, and (b) to what plane is that vector parallel? | |
| 95. |
A particle P travels with constant speed on a circle of radius  (Fig. 4-56) and completes one revolution in 20.0 s. The particle passes through O at time  . State the following vectors in magnitude-angle notation (angle relative to the positive direction of x). With respect to O, find the particle’s position vector at the times t of (a) 5.00 s, (b) 7.50 s, and (c) 10.0 s.
(d) For the 5.00 s interval from the end of the fifth second to the end of the tenth second, find the particle’s displacement. For that interval, find (e) its average velocity and its velocity at the (f) beginning and (g) end. Next, find the acceleration at the (h) beginning and (i) end of that interval. | |
| 96. |
An iceboat sails across the surface of a frozen lake with constant acceleration produced by the wind. At a certain instant the boat’s velocity is  . Three seconds later, because of a wind shift, the boat is instantaneously at rest. What is its average acceleration for this 3 s interval? | |
| 97. |
In 3.50 h, a balloon drifts 21.5 km north, 9.70 km east, and 2.88 km upward from its release point on the ground. Find (a) the magnitude of its average velocity and (b) the angle its average velocity makes with the horizontal.
| |
| 98. |
A ball is thrown horizontally from a height of 20 m and hits the ground with a speed that is three times its initial speed. What is the initial speed?
| |
| 99. |
A projectile is launched with an initial speed of 30 m/s at an angle of 60° above the horizontal. What are the (a) magnitude and (b) angle of its velocity 2.0 s after launch, and (c) is the angle above or below the horizontal? What are the (d) magnitude and (e) angle of its velocity 5.0 s after launch, and (f) is the angle above or below the horizontal?
| |
| 100. |
An airport terminal has a moving sidewalk to speed passengers through a long corridor. Larry does not use the moving sidewalk; he takes 150 s to walk through the corridor. Curly, who simply stands on the moving sidewalk, covers the same distance in 70 s. Moe boards the sidewalk and walks along it. How long does Moe take to move through the corridor? Assume that Larry and Moe walk at the same speed.
| |
| 101. |
A football player punts the football so that it will have a “hang time” (time of flight) of 4.5 s and land 46 m away. If the ball leaves the player’s foot 150 cm above the ground, what must be the (a) magnitude and (b) angle (relative to the horizontal) of the ball’s initial velocity?
| |
| 102. |
For women’s volleyball the top of the net is 2.24 m above the floor and the court measures 9.0 m by 9.0 m on each side of the net. Using a jump serve, a player strikes the ball at a point that is 3.0 m above the floor and a horizontal distance of 8.0 m from the net. If the initial velocity of the ball is horizontal, (a) what minimum magnitude must it have if the ball is to clear the net and (b) what maximum magnitude can it have if the ball is to strike the floor inside the back line on the other side of the net?
| |
| 103. |
Figure 4-57 shows the straight path of a particle across an xy coordinate system as the particle is accelerated from rest during time interval  . The acceleration is constant. The xy coordinates for point A are (4.00 m, 6.00 m); those for point B are (12.0 m, 18.0 m). (a) What is the ratio  of the acceleration components? (b) What are the coordinates of the particle if the motion is continued for another interval equal to  ? | |
| 104. |
An astronaut is rotated in a horizontal centrifuge at a radius of 5.0 m. (a) What is the astronaut’s speed if the centripetal acceleration has a magnitude of 7.0g? (b) How many revolutions per minute are required to produce this acceleration? (c) What is the period of the motion?
| |
| 105. |
(a) What is the magnitude of the centripetal acceleration of an object on Earth’s equator due to the rotation of Earth? (b) What would Earth’s rotation period have to be for objects on the equator to have a centripetal acceleration of magnitude  ? | |
| 106. |
A person walks up a stalled 15-m-long escalator in 90 s. When standing on the same escalator, now moving, the person is carried up in 60 s. How much time would it take that person to walk up the moving escalator? Does the answer depend on the length of the escalator?
| |
| 107. |
A baseball is hit at ground level. The ball reaches its maximum height above ground level 3.0 s after being hit. Then 2.5 s after reaching its maximum height, the ball barely clears a fence that is 97.5 m from where it was hit. Assume the ground is level. (a) What maximum height above ground level is reached by the ball? (b) How high is the fence? (c) How far beyond the fence does the ball strike the ground?
|  | |
| 108. |
The range of a projectile depends not only on  and  but also on the value g of the free-fall acceleration, which varies from place to place. In 1936, Jesse Owens established a world’s running broad jump record of 8.09 m at the Olympic Games at Berlin (where  ). Assuming the same values of  and  , by how much would his record have differed if he had competed instead in 1956 at Melbourne (where  )? 
| |
| 109. |
During volcanic eruptions, chunks of solid rock can be blasted out of the volcano; these projectiles are called volcanic bombs. Figure 4-58 shows a cross section of Mt. Fuji, in Japan. (a) At what initial speed would a bomb have to be ejected, at angle  to the horizontal, from the vent at A in order to fall at the foot of the volcano at B, at vertical distance  and horizontal distance  ? Ignore, for the moment, the effects of air on the bomb’s travel. (b) What would be the time of flight? (c) Would the effect of the air increase or decrease your answer in (a)? | |
| 110. |
Long flights at midlatitudes in the Northern Hemisphere encounter the jet stream, an eastward airflow that can affect a plane’s speed relative to Earth’s surface. If a pilot maintains a certain speed relative to the air (the plane’s airspeed), the speed relative to the surface (the plane’s ground speed) is more when the flight is in the direction of the jet stream and less when the flight is opposite the jet stream. Suppose a round-trip flight is scheduled between two cities separated by 4000 km, with the outgoing flight in the direction of the jet stream and the return flight opposite it. The airline computer advises an airspeed of 1000 km/h, for which the difference in flight times for the outgoing and return flights is 70.0 min. What jet-stream speed is the computer using?
| |
| 111. |
A particle starts from the origin at  with a velocity of  and moves in the xy plane with constant acceleration  . When the particle’s x coordinate is 29 m, what are its (a) y coordinate and (b) speed? |  | |
| 112. |
A sprinter running on a circular track has a velocity of constant magnitude 9.2 m/s and a centripetal acceleration of magnitude  . What are (a) the track radius and (b) the period of the circular motion? | |
| 113. |
An electron having an initial horizontal velocity of magnitude  travels into the region between two horizontal metal plates that are electrically charged. In that region, the electron travels a horizontal distance of 2.00 cm and has a constant downward acceleration of magnitude  due to the charged plates. Find (a) the time the electron takes to travel the 2.00 cm, (b) the vertical distance it travels during that time, and the magnitudes of its (c) horizontal and (d) vertical velocity components as it emerges from the region. | |
| 114. |
An elevator without a ceiling is ascending with a constant speed of 10 m/s. A boy on the elevator shoots a ball directly upward, from a height of 2.0 m above the elevator floor, just as the elevator floor is 28 m above the ground. The initial speed of the ball with respect to the elevator is 20 m/s. (a) What maximum height above the ground does the ball reach? (b) How long does the ball take to return to the elevator floor?
| |
| 115. |
Suppose that a space probe can withstand the stresses of a 20g acceleration. (a) What is the minimum turning radius of such a craft moving at a speed of one-tenth the speed of light? (b) How long would it take to complete a 90° turn at this speed?
| |
| 116. |
At what initial speed must the basketball player in Fig. 4-59 throw the ball, at angle  above the horizontal, to make the foul shot? The horizontal distances are  and  , and the heights are  and  . | |
| 117. |
A wooden boxcar is moving along a straight railroad track at speed  . A sniper fires a bullet (initial speed  ) at it from a high-powered rifle. The bullet passes through both lengthwise walls of the car, its entrance and exit holes being exactly opposite each other as viewed from within the car. From what direction, relative to the track, is the bullet fired? Assume that the bullet is not deflected upon entering the car, but that its speed decreases by 20%.Take  and  . (Why don’t you need to know the width of the boxcar?) | |
| 118. |
You are to throw a ball with a speed of 12.0 m/s at a target that is height  above the level at which you release the ball (Fig. 4-60). You want the ball’s velocity to be horizontal at the instant it reaches the target. (a) At what angle  above the horizontal must you throw the ball? (b) What is the horizontal distance from the release point to the target? (c) What is the speed of the ball just as it reaches the target? | |
| 119. |
Figure 4-61 shows the path taken by a drunk skunk over level ground, from initial point i to final point f. The angles are  ,  , and  , and the distances are  ,  , and  . What are the (a) magnitude and (b) angle of the skunk’s displacement from i to f? | |
| 120. |
A projectile is fired with an initial speed  from level ground at a target that is on the ground, at distance  , as shown in Fig. 4-62. What are the (a) least and (b) greatest launch angles that will allow the projectile to hit the target? | |
| 121. |
Oasis A is 90 km due west of oasis B. A desert camel leaves A and takes 50 h to walk 75 km at 37° north of due east. Next it takes 35 h to walk 65 km due south. Then it rests for 5.0 h. What are the (a) magnitude and (b) direction of the camel’s displacement relative to A at the resting point? From the time the camel leaves A until the end of the rest period, what are the (c) magnitude and (d) direction of its average velocity and (e) its average speed? The camel’s last drink was at A; it must be at B no more than 120 h later for its next drink. If it is to reach B just in time, what must be the (f) magnitude and (g) direction of its average velocity after the rest period?
|  | |
| 122. |
A graphing surprise. At time  , a burrito is launched from level ground, with an initial speed of 16.0 m/s and launch angle  . Imagine a position vector  continuously directed from the launching point to the burrito during the flight. Graph the magnitude r of the position vector for (a)  and (b)  . For  , (c) when does r reach its maximum value, (d) what is that value, and how far (e) horizontally and (f) vertically is the burrito from the launch point? For  , (g) when does r reach its maximum value, (h) what is that value, and how far (i) horizontally and (j) vertically is the burrito from the launch point?
| |
| 123. |
In Sample Problem 4-7b, a ball is shot through a horizontal distance of 686 m by a cannon located at sea level and angled at 45° from the horizontal. How much greater would the horizontal distance have been had the cannon been 30 m higher? | |
| 124. |
(a) If an electron is projected horizontally with a speed of  , how far will it fall in traversing 1.0 m of horizontal distance? (b) Does the answer increase or decrease if the initial speed is increased? | |
| 125. |
The magnitude of the velocity of a projectile when it is at its maximum height above ground level is 10 m/s. (a) What is the magnitude of the velocity of the projectile 1.0 s before it achieves its maximum height? (b) What is the magnitude of the velocity of the projectile 1.0 s after it achieves its maximum height? If we take  and  to be at the point of maximum height and positive x to be in the direction of the velocity there, what are the (c) x coordinate and (d) y coordinate of the projectile 1.0 s before it reaches its maximum height and the (e) x coordinate and (f) y coordinate 1.0 s after it reaches its maximum height? | |
| 126. |
A frightened rabbit moving at 6.0 m/s due east runs onto a large area of level ice of negligible friction. As the rabbit slides across the ice, the force of the wind causes it to have a constant acceleration of  , due north. Choose a coordinate system with the origin at the rabbit’s initial position on the ice and the positive x axis directed toward the east. In unitvector notation, what are the rabbit’s (a) velocity and (b) position when it has slid for 3.0 s? | |
| 127. |
The pilot of an aircraft flies due east relative to the ground in a wind blowing 20 km/h toward the south. If the speed of the aircraft in the absence of wind is 70 km/h, what is the speed of the aircraft relative to the ground?
| |
| 128. |
The pitcher in a slow-pitch softball game releases the ball at a point 3.0 ft above ground level. A stroboscopic plot of the position of the ball is shown in Fig. 4-63, where the readings are 0.25 s apart and the ball is released at  . (a) What is the initial speed of the ball? (b) What is the speed of the ball at the instant it reaches its maximum height above ground level? (c) What is that maximum height? | |
| 129. |
The New Hampshire State Police use aircraft to enforce highway speed limits. Suppose that one of the airplanes has a speed of 135 mi/h in still air. It is flying straight north so that it is at all times directly above a north–south highway. A ground observer tells the pilot by radio that a 70.0 mi/h wind is blowing but neglects to give the wind direction. The pilot observes that in spite of the wind the plane can travel 135 mi along the highway in 1.00 h. In other words, the ground speed is the same as if there were no wind. (a) From what direction is the wind blowing? (b) What is the heading of the plane; that is, in what direction does it point?
| |
| 130. |
The position  of a particle moving in the xy plane is given by  , where  is in meters and t is in seconds. (a) Calculate the x and y components of the particle’s position at  , and 4.0 s and sketch the particle’s path in the xy plane for the interval  . (b) Calculate the components of the particle’s velocity at  , 2.0, and 3.0 s. Show that the velocity is tangent to the path of the particle and in the direction the particle is moving at each time by drawing the velocity vectors on the plot of the particle’s path in part (a). (c) Calculate the components of the particle’s acceleration at  , 2.0, and 3.0 s. | |
| 131. |
A golfer tees off from the top of a rise, giving the golf ball an initial velocity of 43 m/s at an angle of 30° above the horizontal. The ball strikes the fairway a horizontal distance of 180 m from the tee. Assume the fairway is level. (a) How high is the rise above the fairway? (b) What is the speed of the ball as it strikes the fairway?
| |
| 132. |
A track meet is held on a planet in a distant solar system. A shot-putter releases a shot at a point 2.0 m above ground level. A stroboscopic plot of the position of the shot is shown in Fig. 4-64, where the readings are 0.50 s apart and the shot is released at time  . (a) What is the initial velocity of the shot in unit-vector notation? (b) What is the magnitude of the free-fall acceleration on the planet? (c) How long after it is released does the shot reach the ground? (d) If an identical throw of the shot is made on the surface of Earth, how long after it is released does it reach the ground? | |
 |
| Copyright © 2008 John Wiley & Sons, Inc. All rights reserved. |
 , which is a vector that extends from a reference point (usually the origin) to the particle. In the unit-vector notation of Section 3-5,
, which is a vector that extends from a reference point (usually the origin) to the particle. In the unit-vector notation of Section 3-5,  can be written
can be written
 ,
, 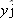 , and
, and 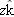 are the vector components of
are the vector components of  and the coefficients x, y, and z are its scalar components.
and the coefficients x, y, and z are its scalar components.
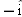 direction. Along the y axis it is 2 m from the origin, in the
direction. Along the y axis it is 2 m from the origin, in the 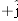 direction. Along the z axis it is 5 m from the origin, in the
direction. Along the z axis it is 5 m from the origin, in the 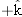 direction.
direction.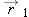 to
to 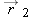 during a certain time interval—then the particle’s displacement
during a certain time interval—then the particle’s displacement  during that time interval is
during that time interval is
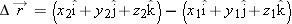
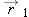 and coordinates (x2, y2, z2) correspond to position vector
and coordinates (x2, y2, z2) correspond to position vector 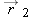 . We can also rewrite the displacement by substituting
. We can also rewrite the displacement by substituting  for (x2 − x1),
for (x2 − x1),  for (y2 − y1), and
for (y2 − y1), and  for (z2 − z1):
for (z2 − z1):
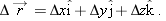
 in a time interval
in a time interval  , then its average velocity
, then its average velocity  is
is
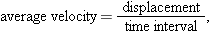
 (the vector on the left side of Eq. 4-8) must be the same as that of the displacement
(the vector on the left side of Eq. 4-8) must be the same as that of the displacement  (the vector on the right side). Using Eq. 4-4, we can write Eq. 4-8 in vector components as
(the vector on the right side). Using Eq. 4-4, we can write Eq. 4-8 in vector components as
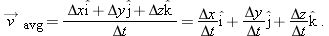
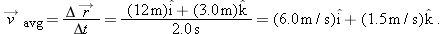
 at some instant. This
at some instant. This  is the value that
is the value that  approaches in the limit as we shrink the time interval
approaches in the limit as we shrink the time interval  to 0 about that instant. Using the language of calculus, we may write
to 0 about that instant. Using the language of calculus, we may write  as the derivative
as the derivative
 , the position vector changes from
, the position vector changes from  to
to  and the particle’s displacement is
and the particle’s displacement is  .
. to 0 about t1. Three things happen as we do so. (1) Position vector
to 0 about t1. Three things happen as we do so. (1) Position vector  in Fig. 4-4 moves toward
in Fig. 4-4 moves toward 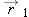 so that
so that  shrinks toward zero. (2) The direction of
shrinks toward zero. (2) The direction of 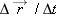 (and thus of
(and thus of  ) approaches the direction of the line tangent to the particle’s path at position 1. (3) The average velocity
) approaches the direction of the line tangent to the particle’s path at position 1. (3) The average velocity  approaches the instantaneous velocity
approaches the instantaneous velocity  at t1.
at t1.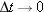 , we have
, we have 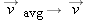 and, most important here,
and, most important here,  takes on the direction of the tangent line. Thus,
takes on the direction of the tangent line. Thus,  has that direction as well:
has that direction as well:
 is always tangent to the particle’s path.
is always tangent to the particle’s path. from Eq. 4-1:
from Eq. 4-1:
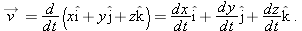
 are
are
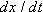 is the scalar component of
is the scalar component of  along the x axis. Thus, we can find the scalar components of
along the x axis. Thus, we can find the scalar components of  by differentiating the scalar components of
by differentiating the scalar components of  .
. and its scalar x and y components. Note that
and its scalar x and y components. Note that  is tangent to the particle’s path at the particle’s position. Caution: When a position vector is drawn, as in Figs. 4-1 through 4-4, it is an arrow that extends from one point (a “here”) to another point (a “there”). However, when a velocity vector is drawn, as in Fig. 4-5, it does not extend from one point to another. Rather, it shows the instantaneous direction of travel of a particle at the tail, and its length (representing the velocity magnitude) can be drawn to any scale.
is tangent to the particle’s path at the particle’s position. Caution: When a position vector is drawn, as in Figs. 4-1 through 4-4, it is an arrow that extends from one point (a “here”) to another point (a “there”). However, when a velocity vector is drawn, as in Fig. 4-5, it does not extend from one point to another. Rather, it shows the instantaneous direction of travel of a particle at the tail, and its length (representing the velocity magnitude) can be drawn to any scale.

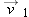 to
to 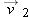 in a time interval
in a time interval  , its average acceleration
, its average acceleration  during
during  is
is
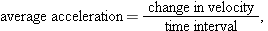
 to zero about some instant, then in the limit
to zero about some instant, then in the limit  approaches the instantaneous acceleration (or acceleration)
approaches the instantaneous acceleration (or acceleration)  at that instant; that is,
at that instant; that is,
 to obtain
to obtain
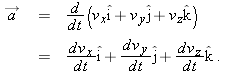
 are
are
 , we differentiate the scalar components of
, we differentiate the scalar components of  .
. and its scalar components for a particle moving in two dimensions. Caution: When an acceleration vector is drawn, as in Fig. 4-7, it does not extend from one position to another. Rather, it shows the direction of acceleration for a particle located at its tail, and its length (representing the acceleration magnitude) can be drawn to any scale.
and its scalar components for a particle moving in two dimensions. Caution: When an acceleration vector is drawn, as in Fig. 4-7, it does not extend from one position to another. Rather, it shows the direction of acceleration for a particle located at its tail, and its length (representing the acceleration magnitude) can be drawn to any scale.

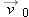 but its acceleration is always the free-fall acceleration
but its acceleration is always the free-fall acceleration 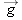 , which is downward. Such a particle is called a projectile (meaning that it is projected or launched), and its motion is called projectile motion. A projectile might be a tennis ball (Fig. 4-9) or baseball in flight, but it is not an airplane or a duck in flight. Many sports (from golf and football to lacrosse and rac-quetball) involve the projectile motion of a ball, and much effort is spent in trying to control that motion for an advantage. For example, the racquetball player who discovered the Z-shot in the 1970s easily won his games because the ball’s peculiar flight to the rear of the court always perplexed his opponents.
, which is downward. Such a particle is called a projectile (meaning that it is projected or launched), and its motion is called projectile motion. A projectile might be a tennis ball (Fig. 4-9) or baseball in flight, but it is not an airplane or a duck in flight. Many sports (from golf and football to lacrosse and rac-quetball) involve the projectile motion of a ball, and much effort is spent in trying to control that motion for an advantage. For example, the racquetball player who discovered the Z-shot in the 1970s easily won his games because the ball’s peculiar flight to the rear of the court always perplexed his opponents. 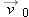 that can be written as
that can be written as
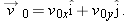
 and
and  can then be found if we know the angle
can then be found if we know the angle  between
between 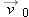 and the positive x direction:
and the positive x direction:
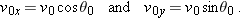
 and velocity vector
and velocity vector  change continuously, but its acceleration vector
change continuously, but its acceleration vector  is constant and always directed vertically downward. The projectile has no horizontal acceleration.
is constant and always directed vertically downward. The projectile has no horizontal acceleration.

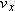 of the projectile’s velocity remains unchanged from its initial value
of the projectile’s velocity remains unchanged from its initial value  throughout the motion, as demonstrated in Fig. 4-13. At any time t, the projectile’s horizontal displacement
throughout the motion, as demonstrated in Fig. 4-13. At any time t, the projectile’s horizontal displacement 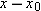 from an initial position
from an initial position 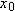 is given by Eq. 2-15 with
is given by Eq. 2-15 with 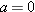 , which we write as
, which we write as
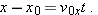
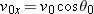 , this becomes
, this becomes
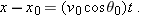
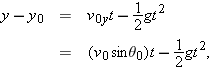
 is replaced with the equivalent
is replaced with the equivalent 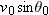 . Similarly, Eqs. 2-11 and 2-16 become
. Similarly, Eqs. 2-11 and 2-16 become
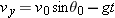

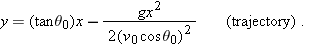
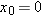 and
and  in Eqs. 4-21 and 4-22, respectively. Because g,
in Eqs. 4-21 and 4-22, respectively. Because g,  , and
, and  are constants, Eq. 4-25 is of the form
are constants, Eq. 4-25 is of the form  , in which a and b are constants. This is the equation of a parabola, so the path is parabolic.
, in which a and b are constants. This is the equation of a parabola, so the path is parabolic.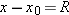 in Eq. 4-21 and
in Eq. 4-21 and 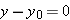 in Eq. 4-22, obtaining
in Eq. 4-22, obtaining
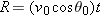
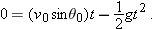
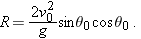
 (see Appendix E), we obtain
(see Appendix E), we obtain
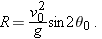


 in unit-vector notation and in magnitude-angle notation?
in unit-vector notation and in magnitude-angle notation?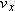 does not change from its initial value
does not change from its initial value 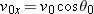 because there is no horizontal acceleration. (3) Component
because there is no horizontal acceleration. (3) Component  changes from its initial value
changes from its initial value 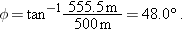 because there is a vertical acceleration.
because there is a vertical acceleration.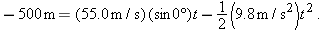 , we also find that when the capsule reaches the water,
, we also find that when the capsule reaches the water,
 are
are
 of 45°. Thus,
of 45°. Thus,
 when the ship is 690 m away. Beyond that distance the ship is safe.
when the ship is 690 m away. Beyond that distance the ship is safe. is
is
 ) in time
) in time
 and
and  .
. of a moving particle is always tangent to the particle’s path at the particle’s position. In Fig. 4-20a, that means
of a moving particle is always tangent to the particle’s path at the particle’s position. In Fig. 4-20a, that means  is perpendicular to a radius r drawn to the particle’s position. Then the angle
is perpendicular to a radius r drawn to the particle’s position. Then the angle  that
that  makes with a vertical at p equals the angle
makes with a vertical at p equals the angle  that radius r makes with the x axis.
that radius r makes with the x axis. are shown in Fig. 4-20b. With them, we can write the velocity
are shown in Fig. 4-20b. With them, we can write the velocity  as
as
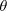
 with
with  and
and 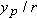 with
with 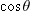 to write
to write
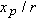
 of particle p, we must take the time derivative of this equation. Noting that speed v and radius r do not change with time, we obtain
of particle p, we must take the time derivative of this equation. Noting that speed v and radius r do not change with time, we obtain
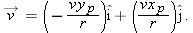
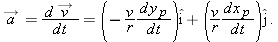 at which
at which 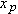 changes is equal to the velocity component
changes is equal to the velocity component  . Similarly,
. Similarly, 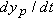 , and, again from Fig. 4-20b, we see that
, and, again from Fig. 4-20b, we see that 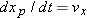 and
and 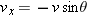 . Making these substitutions in Eq. 4-38, we find
. Making these substitutions in Eq. 4-38, we find
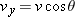
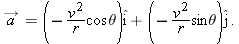
 , we find the angle
, we find the angle 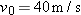 shown in Fig. 4-20c:
shown in Fig. 4-20c:
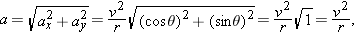
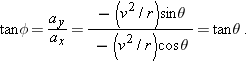 , which means that
, which means that  is directed along the radius r of Fig. 4-20a, toward the circle’s center, as we wanted to prove.
is directed along the radius r of Fig. 4-20a, toward the circle’s center, as we wanted to prove.

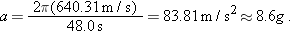
 of P as measured by A is equal to the coordinate
of P as measured by A is equal to the coordinate  of P as measured by B plus the coordinate
of P as measured by B plus the coordinate  of B as measured by A.” Note how this reading is supported by the sequence of the subscripts.
of B as measured by A.” Note how this reading is supported by the sequence of the subscripts.
 of P as measured by A is equal to the velocity
of P as measured by A is equal to the velocity  of P as measured by B plus the velocity
of P as measured by B plus the velocity  of B as measured by A.” The term
of B as measured by A.” The term  is the velocity of frame B relative to frame A.
is the velocity of frame B relative to frame A. relative to Alex (frame A). Car P (the moving particle), however, can change speed and direction (that is, it can accelerate).
relative to Alex (frame A). Car P (the moving particle), however, can change speed and direction (that is, it can accelerate).
 is constant, the last term is zero and we have
is constant, the last term is zero and we have
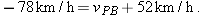 at constant acceleration, what is its acceleration
at constant acceleration, what is its acceleration 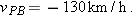 relative to Alex?
relative to Alex? to relate the acceleration to the initial and final velocities of P.
to relate the acceleration to the initial and final velocities of P.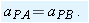 and the final velocity is 0. Thus,
and the final velocity is 0. Thus,
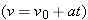 of car P relative to Barbara during the braking?
of car P relative to Barbara during the braking?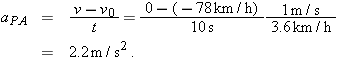 . The final velocity of P relative to Barbara is −52 km/h (this is the velocity of the stopped car relative to the moving Barbara). Thus,
. The final velocity of P relative to Barbara is −52 km/h (this is the velocity of the stopped car relative to the moving Barbara). Thus,
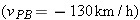 relative to A. (The corresponding axes of these two frames remain parallel.) Figure 4-22 shows a certain instant during the motion. At that instant, the position vector of the origin of B relative to the origin of A is
relative to A. (The corresponding axes of these two frames remain parallel.) Figure 4-22 shows a certain instant during the motion. At that instant, the position vector of the origin of B relative to the origin of A is 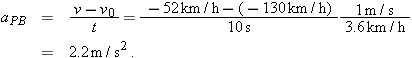 . Also, the position vectors of particle P are
. Also, the position vectors of particle P are  relative to the origin of A and
relative to the origin of A and 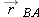 relative to the origin of B. From the arrangement of heads and tails of those three position vectors, we can relate the vectors with
relative to the origin of B. From the arrangement of heads and tails of those three position vectors, we can relate the vectors with
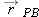 and
and 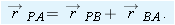 of particle P relative to our observers:
of particle P relative to our observers:
 and
and 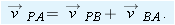 of the particle P relative to our observers. However, note that because
of the particle P relative to our observers. However, note that because 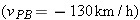 is constant, its time derivative is zero. Thus, we get
is constant, its time derivative is zero. Thus, we get
 , which in unit-vector notation is
, which in unit-vector notation is

 ,
, 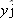 , and
, and 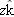 are the vector components of position vector
are the vector components of position vector  , and x, y, and z are its scalar components (as well as the coordinates of the particle). A position vector is described either by a magnitude and one or two angles for orientation, or by its vector or scalar components.
, and x, y, and z are its scalar components (as well as the coordinates of the particle). A position vector is described either by a magnitude and one or two angles for orientation, or by its vector or scalar components.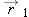 to
to 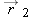 , the particle’s displacement
, the particle’s displacement  is
is
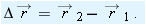
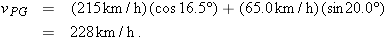
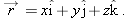
 in time interval
in time interval  , its average velocity
, its average velocity  for that time interval is
for that time interval is

 in Eq. 4-8 is shrunk to 0,
in Eq. 4-8 is shrunk to 0,  reaches a limit called either the velocity or the instantaneous velocity
reaches a limit called either the velocity or the instantaneous velocity  :
:
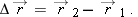
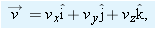
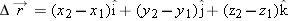 ,
, 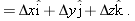 , and
, and  . The instantaneous velocity
. The instantaneous velocity  of a particle is always directed along the tangent to the particle’s path at the particle’s position.
of a particle is always directed along the tangent to the particle’s path at the particle’s position.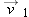 to
to 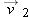 in time interval
in time interval  , its average acceleration during
, its average acceleration during  is
is
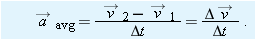
 in Eq. 4-15 is shrunk to 0,
in Eq. 4-15 is shrunk to 0,  reaches a limiting value called either the acceleration or the instantaneous acceleration
reaches a limiting value called either the acceleration or the instantaneous acceleration  :
:
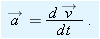
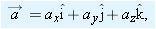
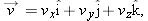 ,
,  , and
, and 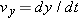 .
.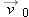 . During its flight, the particle’s horizontal acceleration is zero and its vertical acceleration is the free-fall acceleration −g. (Upward is taken to be a positive direction.) If
. During its flight, the particle’s horizontal acceleration is zero and its vertical acceleration is the free-fall acceleration −g. (Upward is taken to be a positive direction.) If 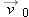 is expressed as a magnitude (the speed
is expressed as a magnitude (the speed  ) and an angle
) and an angle  (measured from the horizontal), the particle’s equations of motion along the horizontal x axis and vertical y axis are
(measured from the horizontal), the particle’s equations of motion along the horizontal x axis and vertical y axis are

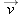
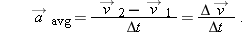

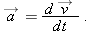
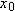 and
and 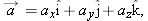 of Eqs. 4-21 to 4-24 are zero. The particle’s horizontal range R, which is the horizontal distance from the launch point to the point at which the particle returns to the launch height, is
of Eqs. 4-21 to 4-24 are zero. The particle’s horizontal range R, which is the horizontal distance from the launch point to the point at which the particle returns to the launch height, is
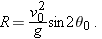
 of constant magnitude
of constant magnitude

 is toward the center of the circle or circular arc, and
is toward the center of the circle or circular arc, and  is said to be centripetal. The time for the particle to complete a circle is
is said to be centripetal. The time for the particle to complete a circle is
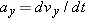
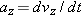
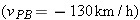 is the velocity of B with respect to A. Both observers measure the same acceleration for the particle:
is the velocity of B with respect to A. Both observers measure the same acceleration for the particle:
 , (2)
, (2) 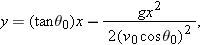 , (3)
, (3)  , (4)
, (4) 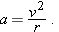 . In your coordinate system, x runs along level ground and y increases upward. (a) Rank the vectors according to the launch speed of the projectile, greatest first. (b) Rank the vectors according to the time of flight of the projectile, greatest first.
. In your coordinate system, x runs along level ground and y increases upward. (a) Rank the vectors according to the launch speed of the projectile, greatest first. (b) Rank the vectors according to the time of flight of the projectile, greatest first. between its velocity vector and its acceleration vector during flight. (a) Which of the lettered points on that curve corresponds to the landing of the fruitcake on the ground? (b) Curve 2 is a similar plot for the same launch speed but for a different launch angle. Does the fruitcake now land farther away or closer to the launch point?
between its velocity vector and its acceleration vector during flight. (a) Which of the lettered points on that curve corresponds to the landing of the fruitcake on the ground? (b) Curve 2 is a similar plot for the same launch speed but for a different launch angle. Does the fruitcake now land farther away or closer to the launch point?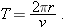 . Rank the three lettered points on the plot according to (a) the total flight time of the ball and (b) the ball’s speed at maximum height, greatest first.
. Rank the three lettered points on the plot according to (a) the total flight time of the ball and (b) the ball’s speed at maximum height, greatest first. is the vertical component
is the vertical component 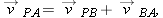 of the position vector greatest in magnitude? (b) At what values of
of the position vector greatest in magnitude? (b) At what values of  is the vertical component
is the vertical component  of the particle’s velocity greatest in magnitude? (c) At what values of
of the particle’s velocity greatest in magnitude? (c) At what values of  is the vertical component
is the vertical component 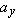 of the particle’s acceleration greatest in magnitude?
of the particle’s acceleration greatest in magnitude? , ending with the position vector
, ending with the position vector  , in meters. What was the positron’s initial position vector?
, in meters. What was the positron’s initial position vector? ,
,  , and
, and  . Find its position vector (a) in unit-vector notation and as (b) a magnitude and (c) an angle relative to the positive direction of the x axis. (d) Sketch the vector on a right-handed coordinate system. If the seed is moved to the xyz coordinates (3.00 m, 0 m, 0 m), what is its displacement (e) in unit-vector notation and as (f) a magnitude and (g) an angle relative to the positive x direction?
. Find its position vector (a) in unit-vector notation and as (b) a magnitude and (c) an angle relative to the positive direction of the x axis. (d) Sketch the vector on a right-handed coordinate system. If the seed is moved to the xyz coordinates (3.00 m, 0 m, 0 m), what is its displacement (e) in unit-vector notation and as (f) a magnitude and (g) an angle relative to the positive x direction? . (a) Find the magnitude of
. (a) Find the magnitude of  . (b) Sketch the vector on a right-handed coordinate system.
. (b) Sketch the vector on a right-handed coordinate system. , and 10 s later it is
, and 10 s later it is  , all in meters. In unit-vector notation, what is its
, all in meters. In unit-vector notation, what is its  during the 10 s?
during the 10 s? , with t in seconds and
, with t in seconds and  in meters. (a) In unit-vector notation, what is the electron’s velocity
in meters. (a) In unit-vector notation, what is the electron’s velocity  ? At
? At  , what is
, what is  (b) in unit-vector notation and as (c) a magnitude and (d) an angle relative to the positive direction of the x axis?
(b) in unit-vector notation and as (c) a magnitude and (d) an angle relative to the positive direction of the x axis? ), to points B (at
), to points B (at  ), C (at
), C (at  ), and finally D (at
), and finally D (at  ). Consider the average velocities of the squirrel from point A to each of the other three points. Of them, what are the (a) magnitude and (b) angle of the one with the least magnitude and the (c) magnitude and (d) angle of the one with the greatest magnitude?
). Consider the average velocities of the squirrel from point A to each of the other three points. Of them, what are the (a) magnitude and (b) angle of the one with the least magnitude and the (c) magnitude and (d) angle of the one with the greatest magnitude? locates a particle as a function of time t. Vector
locates a particle as a function of time t. Vector  is in meters, t is in seconds, and factors e and f are constants. Figure 4-34 gives the angle
is in meters, t is in seconds, and factors e and f are constants. Figure 4-34 gives the angle  of the particle’s direction of travel as a function of t (
of the particle’s direction of travel as a function of t ( is measured from the positive x direction). What are (a) e and (b) f, including units?
is measured from the positive x direction). What are (a) e and (b) f, including units? . Write expressions for (a) its velocity and (b) its acceleration as functions of time.
. Write expressions for (a) its velocity and (b) its acceleration as functions of time.  and then 4.0 s later has
and then 4.0 s later has  (in meters per second). For that 4.0 s, what are (a) the proton’s average acceleration
(in meters per second). For that 4.0 s, what are (a) the proton’s average acceleration  in unit-vector notation, (b) the magnitude of
in unit-vector notation, (b) the magnitude of  , and (c) the angle between
, and (c) the angle between  and the positive direction of the x axis?
and the positive direction of the x axis? of a particle moving in an xy plane is given by
of a particle moving in an xy plane is given by  , with
, with  in meters and t in seconds. In unit-vector notation, calculate (a)
in meters and t in seconds. In unit-vector notation, calculate (a)  , (b)
, (b)  , and (c)
, and (c)  for
for  . (d) What is the angle between the positive direction of the x axis and a line tangent to the particle’s path at
. (d) What is the angle between the positive direction of the x axis and a line tangent to the particle’s path at  ?
? 
 and
and  . Its initial velocity has components
. Its initial velocity has components  and
and  . In unit-vector notation, what is the velocity of the cart when it reaches its greatest y coordinate?
. In unit-vector notation, what is the velocity of the cart when it reaches its greatest y coordinate? . At time
. At time  , the velocity is
, the velocity is  . What are the (a) magnitude and (b) angle of its velocity when it has been displaced by 12.0 m parallel to the x axis?
. What are the (a) magnitude and (b) angle of its velocity when it has been displaced by 12.0 m parallel to the x axis? and a constant acceleration
and a constant acceleration  . When it reaches its maximum x coordinate, what are its (a) velocity and (b) position vector?
. When it reaches its maximum x coordinate, what are its (a) velocity and (b) position vector?  of a particle moving in the xy plane is given by
of a particle moving in the xy plane is given by  , with
, with  in meters per second and t (> 0) in seconds. (a) What is the acceleration when
in meters per second and t (> 0) in seconds. (a) What is the acceleration when  ? (b) When (if ever) is the acceleration zero? (c) When (if ever) is the velocity zero? (d) When (if ever) does the speed equal 10 m/s?
? (b) When (if ever) is the acceleration zero? (c) When (if ever) is the velocity zero? (d) When (if ever) does the speed equal 10 m/s? , where
, where  is in meters per second-squared and t is in seconds. At
is in meters per second-squared and t is in seconds. At  , the position vector
, the position vector  locates the paticle, which then has the velocity vector
locates the paticle, which then has the velocity vector  . At
. At  , what are (a) its position vector in unit-vector notation and (b) the angle between its direction of travel and the positive direction of the x axis?
, what are (a) its position vector in unit-vector notation and (b) the angle between its direction of travel and the positive direction of the x axis? with a constant velocity
with a constant velocity  of magnitude 3.0 m/s and parallel to the x axis. At the instant particle A passes the y axis, particle B leaves the origin with zero initial speed and constant acceleration
of magnitude 3.0 m/s and parallel to the x axis. At the instant particle A passes the y axis, particle B leaves the origin with zero initial speed and constant acceleration  of magnitude
of magnitude  . What angle
. What angle  between
between  and the positive direction of the y axis would result in a collision?
and the positive direction of the y axis would result in a collision? in Tokyo. How much less was Powell’s range than the maximum possible range for a particle launched at the same speed?
in Tokyo. How much less was Powell’s range than the maximum possible range for a particle launched at the same speed?
 above the horizontal. The stone strikes at A, 5.50 s after launching. Find (a) the height h of the cliff, (b) the speed of the stone just before impact at A, and (c) the maximum height H reached above the ground.
above the horizontal. The stone strikes at A, 5.50 s after launching. Find (a) the height h of the cliff, (b) the speed of the stone just before impact at A, and (c) the maximum height H reached above the ground. below the horizontal when the pilot releases a radar decoy (Fig. 4-37).The horizontal distance between the release point and the point where the decoy strikes the ground
below the horizontal when the pilot releases a radar decoy (Fig. 4-37).The horizontal distance between the release point and the point where the decoy strikes the ground  . (a) How long is the decoy in the air? (b) How high was the release point?
. (a) How long is the decoy in the air? (b) How high was the release point?  , with an initial velocity of magnitude 20.0 m/s and at an angle of 40.0° above the horizontal. What are the magnitudes of the (a) horizontal and (b) vertical components of its displacement from the catapult site at
, with an initial velocity of magnitude 20.0 m/s and at an angle of 40.0° above the horizontal. What are the magnitudes of the (a) horizontal and (b) vertical components of its displacement from the catapult site at  ? Repeat for the (c) horizontal and (d) vertical components at
? Repeat for the (c) horizontal and (d) vertical components at  , and for the (e) horizontal and (f) vertical components at
, and for the (e) horizontal and (f) vertical components at  .
. and at an angle of
and at an angle of  . What is the speed of the stone if it hits the wall (a) just as it reaches the top of its parabolic path and (b) when it has descended to half that height? (c) As a percentage, how much faster is it moving in part (b) than in part (a)?
. What is the speed of the stone if it hits the wall (a) just as it reaches the top of its parabolic path and (b) when it has descended to half that height? (c) As a percentage, how much faster is it moving in part (b) than in part (a)?
 .
. and at a height of 2.160 m. What horizontal distance would the shot travel if the launch angle
and at a height of 2.160 m. What horizontal distance would the shot travel if the launch angle  is (a) 45.00° and (b) 42.00°? The answers indicate that the angle of 45°, which maximizes the range of projectile motion, does not maximize the horizontal distance when the launch and landing are at different heights.
is (a) 45.00° and (b) 42.00°? The answers indicate that the angle of 45°, which maximizes the range of projectile motion, does not maximize the horizontal distance when the launch and landing are at different heights.
 , with
, with  horizontal and
horizontal and  upward. (a) To what maximum height does the ball rise? (b) What total horizontal distance does the ball travel? What are the (c) magnitude and (d) angle (below the horizontal) of the ball’s velocity just before it hits the ground?
upward. (a) To what maximum height does the ball rise? (b) What total horizontal distance does the ball travel? What are the (c) magnitude and (d) angle (below the horizontal) of the ball’s velocity just before it hits the ground?  above the horizontal (Fig. 4-38). The wall is distance
above the horizontal (Fig. 4-38). The wall is distance  from the release point of the ball. (a) How far above the release point does the ball hit the wall? What are the (b) horizontal and (c) vertical components of its velocity as it hits the wall? (d) When it hits, has it passed the highest point on its trajectory?
from the release point of the ball. (a) How far above the release point does the ball hit the wall? What are the (b) horizontal and (c) vertical components of its velocity as it hits the wall? (d) When it hits, has it passed the highest point on its trajectory? from the building and at angle
from the building and at angle  with the horizontal. (a) Find h (Hint: One way is to reverse the motion, as if on videotape.) What are the (b) magnitude and (c) angle relative to the horizontal of the velocity at which the ball is thrown? (d) Is the angle above or below the horizontal?
with the horizontal. (a) Find h (Hint: One way is to reverse the motion, as if on videotape.) What are the (b) magnitude and (c) angle relative to the horizontal of the velocity at which the ball is thrown? (d) Is the angle above or below the horizontal? at the instant the ball is struck. (a) How far does the golf ball travel horizontally before returning to ground level? (b) What is the maximum height above ground level attained by the ball?
at the instant the ball is struck. (a) How far does the golf ball travel horizontally before returning to ground level? (b) What is the maximum height above ground level attained by the ball? and height
and height  . A plateau is located at the top of the ramp. (a) Does the ball land on the ramp or the plateau? When it lands, what are the (b) magnitude and (c) angle of its displacement from the launch point?
. A plateau is located at the top of the ramp. (a) Does the ball land on the ramp or the plateau? When it lands, what are the (b) magnitude and (c) angle of its displacement from the launch point? and distance d, a drop must be launched at a different angle
and distance d, a drop must be launched at a different angle  if its parabolic path is to intersect the insect. If
if its parabolic path is to intersect the insect. If  ,
,  , and the launch speed is 3.56 m/s, what
, and the launch speed is 3.56 m/s, what  is required for the drop to be at the top of the parabolic path when it reaches the insect?
is required for the drop to be at the top of the parabolic path when it reaches the insect?  above the release level. The ball’s path just before landing is angled at
above the release level. The ball’s path just before landing is angled at  with the roof. (a) Find the horizontal distance d it travels. (See the hint to Problem 41.) What are the (b) magnitude and (c) angle (relative to the horizontal) of the ball’s initial velocity?
with the roof. (a) Find the horizontal distance d it travels. (See the hint to Problem 41.) What are the (b) magnitude and (c) angle (relative to the horizontal) of the ball’s initial velocity? at an angle of
at an angle of  , what percent of the jump’s range does the player spend in the upper half of the jump (between maximum height and half maximum height)?
, what percent of the jump’s range does the player spend in the upper half of the jump (between maximum height and half maximum height)?
 , the launch angle is
, the launch angle is  , the initial course is approximately flat, and the steeper track has a slope of 11.3°. Figure 4-45a shows a prejump that allows the skier to land on the top portion of the steeper track. Figure 4-45b shows a jump at the edge of the steeper track. In Fig. 4-45a, the skier lands at approximately the launch level, (a) In the landing, what is the angle
, the initial course is approximately flat, and the steeper track has a slope of 11.3°. Figure 4-45a shows a prejump that allows the skier to land on the top portion of the steeper track. Figure 4-45b shows a jump at the edge of the steeper track. In Fig. 4-45a, the skier lands at approximately the launch level, (a) In the landing, what is the angle  between the skier’s path and the slope? In Fig. 4-45b, (b) how far below the launch level does the skier land and (c) what is
between the skier’s path and the slope? In Fig. 4-45b, (b) how far below the launch level does the skier land and (c) what is  ? (The greater fall and greater
? (The greater fall and greater  can result in loss of control in the landing.)
can result in loss of control in the landing.)
 . The value of
. The value of  determines the flight time; let
determines the flight time; let  represent the maximum flight time. What is the least speed the ball will have during its flight if
represent the maximum flight time. What is the least speed the ball will have during its flight if  is chosen such that the flight time is
is chosen such that the flight time is  ?
?
 and then caught at the same height. It travels alongside a wall, moving up past the top of the wall 1.00 s after it is hit and then down past the top of the wall 4.00 s later, at distance
and then caught at the same height. It travels alongside a wall, moving up past the top of the wall 1.00 s after it is hit and then down past the top of the wall 4.00 s later, at distance  farther along the wall. (a) What horizontal distance is traveled by the ball from hit to catch? What are the (b) magnitude and (c) angle (relative to the horizontal) of the ball’s velocity just after being hit? (d) How high is the wall?
farther along the wall. (a) What horizontal distance is traveled by the ball from hit to catch? What are the (b) magnitude and (c) angle (relative to the horizontal) of the ball’s velocity just after being hit? (d) How high is the wall?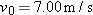 and radius
and radius  . At
. At  his acceleration is
his acceleration is  . At that instant, what are the values of (a)
. At that instant, what are the values of (a)  and (b)
and (b)  ?
? of magnitude
of magnitude  . Position vector
. Position vector  locates him relative to the rotation axis. (a) What is the magnitude of
locates him relative to the rotation axis. (a) What is the magnitude of  ? What is the direction of
? What is the direction of  when
when  is directed (b) due east and (c) due south?
is directed (b) due east and (c) due south? . At that instant and in unit-vector notation, what is the acceleration of the wallet?
. At that instant and in unit-vector notation, what is the acceleration of the wallet? , it is at point (5.00 m, 6.00 m) with velocity
, it is at point (5.00 m, 6.00 m) with velocity  and acceleration in the positive x direction. At time
and acceleration in the positive x direction. At time  , it has velocity
, it has velocity  and acceleration in the positive y direction. What are the (a) x and (b) y coordinates of the center of the circular path if
and acceleration in the positive y direction. What are the (a) x and (b) y coordinates of the center of the circular path if  is less than one period?
is less than one period? , the acceleration of a particle in counterclockwise circular motion is
, the acceleration of a particle in counterclockwise circular motion is  . It moves at constant speed. At time
. It moves at constant speed. At time  , its acceleration is
, its acceleration is  . What is the radius of the path taken by the particle if
. What is the radius of the path taken by the particle if  is less than one period?
is less than one period? 
 and an acceleration of
and an acceleration of  . What are the (a) x and (b) y coordinates of the center of the circular path?
. What are the (a) x and (b) y coordinates of the center of the circular path? , the cat’s velocity is
, the cat’s velocity is  , measured on a horizontal xy coordinate system. At
, measured on a horizontal xy coordinate system. At  , its velocity is
, its velocity is  . What are (a) the magnitude of the cat’s centripetal acceleration and (b) the cat’s average acceleration during the time interval
. What are (a) the magnitude of the cat’s centripetal acceleration and (b) the cat’s average acceleration during the time interval  , which is less than one period?
, which is less than one period? relative to himself. If
relative to himself. If  has magnitude 6.0 m/s, what is the smallest angle it can have for the pass to be legal?
has magnitude 6.0 m/s, what is the smallest angle it can have for the pass to be legal?
 from the intersection and moving at speed
from the intersection and moving at speed  . Motorist M is distance
. Motorist M is distance  from the intersection and moving at speed
from the intersection and moving at speed  . (a) In unit-vector notation, what is the velocity of the motorist with respect to the police car? (b) For the instant shown in Fig. 4-49, what is the angle between the velocity found in (a) and the line of sight between the two cars? (c) If the cars maintain their velocities, do the answers to (a) and (b) change as the cars move nearer the intersection?
. (a) In unit-vector notation, what is the velocity of the motorist with respect to the police car? (b) For the instant shown in Fig. 4-49, what is the angle between the velocity found in (a) and the line of sight between the two cars? (c) If the cars maintain their velocities, do the answers to (a) and (b) change as the cars move nearer the intersection? . Relative to the guard, P has accelerated from rest at a constant rate of
. Relative to the guard, P has accelerated from rest at a constant rate of  at the angle
at the angle  . At a certain time during the acceleration, P has a speed of 40.0 m/s. At that time, what are the (a) magnitude and (b) direction of the velocity of P relative to B and the (c) magnitude and (d) direction of the acceleration of P relative to B?
. At a certain time during the acceleration, P has a speed of 40.0 m/s. At that time, what are the (a) magnitude and (b) direction of the velocity of P relative to B and the (c) magnitude and (d) direction of the acceleration of P relative to B? toward the east? (b) Write an expression (in terms of
toward the east? (b) Write an expression (in terms of  and
and  ) for the position of A relative to B as a function of t, where
) for the position of A relative to B as a function of t, where  when the ships are in the positions described above. (c) At what time is the separation between the ships least? (d) What is that least separation?
when the ships are in the positions described above. (c) At what time is the separation between the ships least? (d) What is that least separation? when the asteroid strikes the ground at time
when the asteroid strikes the ground at time  and position
and position  (Fig. 4-51). (a) At
(Fig. 4-51). (a) At  , what are the x and y coordinates of the rocks headed in your direction from launches A through E? (b) Plot these coordinates and then sketch a curve through the points to include rocks with intermediate launch speeds and angles. The curve should indicate what you would see as you look up into the approaching rocks and what dinosaurs must have seen during asteroid strikes long ago.
, what are the x and y coordinates of the rocks headed in your direction from launches A through E? (b) Plot these coordinates and then sketch a curve through the points to include rocks with intermediate launch speeds and angles. The curve should indicate what you would see as you look up into the approaching rocks and what dinosaurs must have seen during asteroid strikes long ago.
 from the floor and at a distance
from the floor and at a distance  from a wall. At what height on the wall does the lump hit?
from a wall. At what height on the wall does the lump hit? . At that instant, what is its velocity in unit-vector notation?
. At that instant, what is its velocity in unit-vector notation? . Simultaneously, a construction elevator cab begins to move upward from the ground with a constant speed of
. Simultaneously, a construction elevator cab begins to move upward from the ground with a constant speed of  . What maximum height does the ball reach relative to (a) the ground and (b) the cab floor? At what rate does the speed of the ball change relative to (c) the ground and (d) the cab floor?
. What maximum height does the ball reach relative to (a) the ground and (b) the cab floor? At what rate does the speed of the ball change relative to (c) the ground and (d) the cab floor? while a ball of ice is shot from the sled with a velocity
while a ball of ice is shot from the sled with a velocity  relative to the sled. When the ball lands, its horizontal displacement
relative to the sled. When the ball lands, its horizontal displacement  relative to the ground (from its launch position to its landing position) is measured. Figure 4-54b gives
relative to the ground (from its launch position to its landing position) is measured. Figure 4-54b gives  as a function of
as a function of  . Assume the ball lands at approximately its launch height. What are the values of (a)
. Assume the ball lands at approximately its launch height. What are the values of (a)  and (b)
and (b)  ? The ball’s displacement
? The ball’s displacement  relative to the sled can also be measured. Assume that the sled’s velocity is not changed when the ball is shot. What is
relative to the sled can also be measured. Assume that the sled’s velocity is not changed when the ball is shot. What is  when
when  is (c) 5.0 m/s and (d) 15 m/s?
is (c) 5.0 m/s and (d) 15 m/s? point directly across the river and
point directly across the river and  point directly downstream. If she rows in a straight line to a point directly opposite her starting position, (a) at what angle to
point directly downstream. If she rows in a straight line to a point directly opposite her starting position, (a) at what angle to  must she point the boat and (b) how long will she take? (c) How long will she take if, instead, she rows 3.2 km down the river and then back to her starting point? (d) How long if she rows 3.2 km up the river and then back to her starting point? (e) At what angle to
must she point the boat and (b) how long will she take? (c) How long will she take if, instead, she rows 3.2 km down the river and then back to her starting point? (d) How long if she rows 3.2 km up the river and then back to her starting point? (e) At what angle to  should she point the boat if she wants to cross the river in the shortest possible time? (f) How long is that shortest time?
should she point the boat if she wants to cross the river in the shortest possible time? (f) How long is that shortest time? from the station and at angle
from the station and at angle  above the horizon. The airplane is tracked through an angular change
above the horizon. The airplane is tracked through an angular change  in the vertical east–west plane; its distance is then
in the vertical east–west plane; its distance is then  . Find the (a) magnitude and (b) direction of the airplane’s displacement during this period.
. Find the (a) magnitude and (b) direction of the airplane’s displacement during this period. in a particular magnetic field. (a) What is the speed of the electron if the radius of its circular path is 15 cm? (b) What is the period of the motion?
in a particular magnetic field. (a) What is the speed of the electron if the radius of its circular path is 15 cm? (b) What is the period of the motion? and then later is
and then later is  , all in meters. (a) What is the proton’s displacement vector, and (b) to what plane is that vector parallel?
, all in meters. (a) What is the proton’s displacement vector, and (b) to what plane is that vector parallel? (Fig. 4-56) and completes one revolution in 20.0 s. The particle passes through O at time
(Fig. 4-56) and completes one revolution in 20.0 s. The particle passes through O at time  . State the following vectors in magnitude-angle notation (angle relative to the positive direction of x). With respect to O, find the particle’s position vector at the times t of (a) 5.00 s, (b) 7.50 s, and (c) 10.0 s.
. State the following vectors in magnitude-angle notation (angle relative to the positive direction of x). With respect to O, find the particle’s position vector at the times t of (a) 5.00 s, (b) 7.50 s, and (c) 10.0 s. . Three seconds later, because of a wind shift, the boat is instantaneously at rest. What is its average acceleration for this 3 s interval?
. Three seconds later, because of a wind shift, the boat is instantaneously at rest. What is its average acceleration for this 3 s interval? . The acceleration is constant. The xy coordinates for point A are (4.00 m, 6.00 m); those for point B are (12.0 m, 18.0 m). (a) What is the ratio
. The acceleration is constant. The xy coordinates for point A are (4.00 m, 6.00 m); those for point B are (12.0 m, 18.0 m). (a) What is the ratio  of the acceleration components? (b) What are the coordinates of the particle if the motion is continued for another interval equal to
of the acceleration components? (b) What are the coordinates of the particle if the motion is continued for another interval equal to  ?
? ?
? and
and  but also on the value g of the free-fall acceleration, which varies from place to place. In 1936, Jesse Owens established a world’s running broad jump record of 8.09 m at the Olympic Games at Berlin (where
but also on the value g of the free-fall acceleration, which varies from place to place. In 1936, Jesse Owens established a world’s running broad jump record of 8.09 m at the Olympic Games at Berlin (where  ). Assuming the same values of
). Assuming the same values of  and
and  , by how much would his record have differed if he had competed instead in 1956 at Melbourne (where
, by how much would his record have differed if he had competed instead in 1956 at Melbourne (where  )?
)? 
 to the horizontal, from the vent at A in order to fall at the foot of the volcano at B, at vertical distance
to the horizontal, from the vent at A in order to fall at the foot of the volcano at B, at vertical distance  and horizontal distance
and horizontal distance  ? Ignore, for the moment, the effects of air on the bomb’s travel. (b) What would be the time of flight? (c) Would the effect of the air increase or decrease your answer in (a)?
? Ignore, for the moment, the effects of air on the bomb’s travel. (b) What would be the time of flight? (c) Would the effect of the air increase or decrease your answer in (a)? with a velocity of
with a velocity of  and moves in the xy plane with constant acceleration
and moves in the xy plane with constant acceleration  . When the particle’s x coordinate is 29 m, what are its (a) y coordinate and (b) speed?
. When the particle’s x coordinate is 29 m, what are its (a) y coordinate and (b) speed?  . What are (a) the track radius and (b) the period of the circular motion?
. What are (a) the track radius and (b) the period of the circular motion? travels into the region between two horizontal metal plates that are electrically charged. In that region, the electron travels a horizontal distance of 2.00 cm and has a constant downward acceleration of magnitude
travels into the region between two horizontal metal plates that are electrically charged. In that region, the electron travels a horizontal distance of 2.00 cm and has a constant downward acceleration of magnitude  due to the charged plates. Find (a) the time the electron takes to travel the 2.00 cm, (b) the vertical distance it travels during that time, and the magnitudes of its (c) horizontal and (d) vertical velocity components as it emerges from the region.
due to the charged plates. Find (a) the time the electron takes to travel the 2.00 cm, (b) the vertical distance it travels during that time, and the magnitudes of its (c) horizontal and (d) vertical velocity components as it emerges from the region. . A sniper fires a bullet (initial speed
. A sniper fires a bullet (initial speed  ) at it from a high-powered rifle. The bullet passes through both lengthwise walls of the car, its entrance and exit holes being exactly opposite each other as viewed from within the car. From what direction, relative to the track, is the bullet fired? Assume that the bullet is not deflected upon entering the car, but that its speed decreases by 20%.Take
) at it from a high-powered rifle. The bullet passes through both lengthwise walls of the car, its entrance and exit holes being exactly opposite each other as viewed from within the car. From what direction, relative to the track, is the bullet fired? Assume that the bullet is not deflected upon entering the car, but that its speed decreases by 20%.Take  and
and  . (Why don’t you need to know the width of the boxcar?)
. (Why don’t you need to know the width of the boxcar?) above the level at which you release the ball (Fig. 4-60). You want the ball’s velocity to be horizontal at the instant it reaches the target. (a) At what angle
above the level at which you release the ball (Fig. 4-60). You want the ball’s velocity to be horizontal at the instant it reaches the target. (a) At what angle  above the horizontal must you throw the ball? (b) What is the horizontal distance from the release point to the target? (c) What is the speed of the ball just as it reaches the target?
above the horizontal must you throw the ball? (b) What is the horizontal distance from the release point to the target? (c) What is the speed of the ball just as it reaches the target? , a burrito is launched from level ground, with an initial speed of 16.0 m/s and launch angle
, a burrito is launched from level ground, with an initial speed of 16.0 m/s and launch angle  . Imagine a position vector
. Imagine a position vector  continuously directed from the launching point to the burrito during the flight. Graph the magnitude r of the position vector for (a)
continuously directed from the launching point to the burrito during the flight. Graph the magnitude r of the position vector for (a)  and (b)
and (b)  . For
. For  , (c) when does r reach its maximum value, (d) what is that value, and how far (e) horizontally and (f) vertically is the burrito from the launch point? For
, (c) when does r reach its maximum value, (d) what is that value, and how far (e) horizontally and (f) vertically is the burrito from the launch point? For  , (g) when does r reach its maximum value, (h) what is that value, and how far (i) horizontally and (j) vertically is the burrito from the launch point?
, (g) when does r reach its maximum value, (h) what is that value, and how far (i) horizontally and (j) vertically is the burrito from the launch point? , how far will it fall in traversing 1.0 m of horizontal distance? (b) Does the answer increase or decrease if the initial speed is increased?
, how far will it fall in traversing 1.0 m of horizontal distance? (b) Does the answer increase or decrease if the initial speed is increased? and
and  to be at the point of maximum height and positive x to be in the direction of the velocity there, what are the (c) x coordinate and (d) y coordinate of the projectile 1.0 s before it reaches its maximum height and the (e) x coordinate and (f) y coordinate 1.0 s after it reaches its maximum height?
to be at the point of maximum height and positive x to be in the direction of the velocity there, what are the (c) x coordinate and (d) y coordinate of the projectile 1.0 s before it reaches its maximum height and the (e) x coordinate and (f) y coordinate 1.0 s after it reaches its maximum height? , due north. Choose a coordinate system with the origin at the rabbit’s initial position on the ice and the positive x axis directed toward the east. In unitvector notation, what are the rabbit’s (a) velocity and (b) position when it has slid for 3.0 s?
, due north. Choose a coordinate system with the origin at the rabbit’s initial position on the ice and the positive x axis directed toward the east. In unitvector notation, what are the rabbit’s (a) velocity and (b) position when it has slid for 3.0 s? . (a) What is the initial speed of the ball? (b) What is the speed of the ball at the instant it reaches its maximum height above ground level? (c) What is that maximum height?
. (a) What is the initial speed of the ball? (b) What is the speed of the ball at the instant it reaches its maximum height above ground level? (c) What is that maximum height? of a particle moving in the xy plane is given by
of a particle moving in the xy plane is given by  , where
, where  is in meters and t is in seconds. (a) Calculate the x and y components of the particle’s position at
is in meters and t is in seconds. (a) Calculate the x and y components of the particle’s position at  , and 4.0 s and sketch the particle’s path in the xy plane for the interval
, and 4.0 s and sketch the particle’s path in the xy plane for the interval  . (b) Calculate the components of the particle’s velocity at
. (b) Calculate the components of the particle’s velocity at  , 2.0, and 3.0 s. Show that the velocity is tangent to the path of the particle and in the direction the particle is moving at each time by drawing the velocity vectors on the plot of the particle’s path in part (a). (c) Calculate the components of the particle’s acceleration at
, 2.0, and 3.0 s. Show that the velocity is tangent to the path of the particle and in the direction the particle is moving at each time by drawing the velocity vectors on the plot of the particle’s path in part (a). (c) Calculate the components of the particle’s acceleration at  , 2.0, and 3.0 s.
, 2.0, and 3.0 s. . (a) What is the initial velocity of the shot in unit-vector notation? (b) What is the magnitude of the free-fall acceleration on the planet? (c) How long after it is released does the shot reach the ground? (d) If an identical throw of the shot is made on the surface of Earth, how long after it is released does it reach the ground?
. (a) What is the initial velocity of the shot in unit-vector notation? (b) What is the magnitude of the free-fall acceleration on the planet? (c) How long after it is released does the shot reach the ground? (d) If an identical throw of the shot is made on the surface of Earth, how long after it is released does it reach the ground?