Our two observers are again watching a moving particle
P from the origins of reference frames
A and
B, while
B moves at a constant velocity
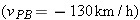
relative to
A. (The corresponding axes of these two frames remain parallel.) Figure
4-22 shows a certain instant during the motion. At that instant, the position vector of the origin of
B relative to the origin of
A is
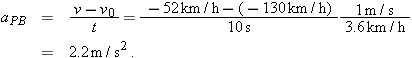
. Also, the position vectors of particle
P are

relative to the origin of
A and
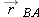
relative to the origin of
B. From the arrangement of heads and tails of those three position vectors, we can relate the vectors with
 |
| (4-43) |
 |
By taking the time derivative of this equation, we can relate the velocities
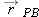
and
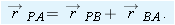
of particle
P relative to our observers:
 |
| (4-44) |
 |
By taking the time derivative of this relation, we can relate the accelerations

and
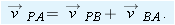
of the particle
P relative to our observers. However, note that because
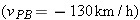
is constant, its time derivative is zero. Thus, we get
 |
| (4-45) |
 |
As for one-dimensional motion, we have the following rule: Observers on different frames of reference that move at constant velocity relative to each other will measure the
same acceleration for a moving particle.
 |  | |  |  | FIGURE 4-22 | Frame B has the constant two-dimensional velocity 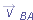 relative to frame A. The position vector of B relative to A is relative to frame A. The position vector of B relative to A is 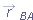 . The position vectors of particle P are . The position vectors of particle P are 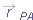 relative to A and relative to A and  relative to B. relative to B.
|
|  |
|  |
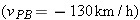 relative to A. (The corresponding axes of these two frames remain parallel.) Figure 4-22 shows a certain instant during the motion. At that instant, the position vector of the origin of B relative to the origin of A is
relative to A. (The corresponding axes of these two frames remain parallel.) Figure 4-22 shows a certain instant during the motion. At that instant, the position vector of the origin of B relative to the origin of A is  . Also, the position vectors of particle P are
. Also, the position vectors of particle P are  relative to the origin of A and
relative to the origin of A and 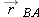 relative to the origin of B. From the arrangement of heads and tails of those three position vectors, we can relate the vectors with
relative to the origin of B. From the arrangement of heads and tails of those three position vectors, we can relate the vectors with
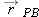 and
and 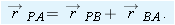 of particle P relative to our observers:
of particle P relative to our observers:
 and
and 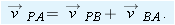 of the particle P relative to our observers. However, note that because
of the particle P relative to our observers. However, note that because 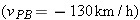 is constant, its time derivative is zero. Thus, we get
is constant, its time derivative is zero. Thus, we get