| CHAPTER 4 |
| Questions |
| ||||
| ||||
| 1. | |
| 2. |
Figure 4-25 shows the path taken by a skunk foraging for trash food, from initial point i. The skunk took the same time T to go from each labeled point to the next along its path. Rank points a, b, and c according to the magnitude of the average velocity of the skunk to reach them from initial point i, greatest first.
| |||||||||||||||
| 3. |
You are to launch a rocket, from just above the ground, with one of the following initial velocity vectors: (1)
 , (2) , (2) 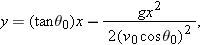 , (3) , (3)  , (4) , (4) 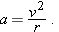 . In your coordinate system, x runs along level ground and y increases upward. (a) Rank the vectors according to the launch speed of the projectile, greatest first. (b) Rank the vectors according to the time of flight of the projectile, greatest first. . In your coordinate system, x runs along level ground and y increases upward. (a) Rank the vectors according to the launch speed of the projectile, greatest first. (b) Rank the vectors according to the time of flight of the projectile, greatest first. |
| 4. |
Figure 4-26 shows three situations in which identical projectiles are launched (at the same level) at identical initial speeds and angles. The projectiles do not land on the same terrain, however. Rank the situations according to the final speeds of the projectiles just before they land, greatest first.
| |||||||||||||||
| 5. |
When Paris was shelled from 100 km away with the WWI long-range artillery piece “Big Bertha,” the shells were fired at an angle greater than 45° to give them a greater range, possibly even twice as long as at 45°. Does that result mean that the air density at high altitudes increases with altitude or decreases?
|
| 6. |
In Fig. 4-27, a cream tangerine is thrown up past windows 1, 2, and 3, which are identical in size and regularly spaced vertically. Rank those three windows according to (a) the time the cream tangerine takes to pass them and (b) the average speed of the cream tangerine during the passage, greatest first.
The cream tangerine then moves down past windows 4, 5, and 6, which are identical in size and irregularly spaced horizontally. Rank those three windows according to (c) the time the cream tangerine takes to pass them and (d) the average speed of the cream tangerine during the passage, greatest first.
| |||||||||||||||
| 7. | |
| 8. |
The only good use of a fruitcake is in catapult practice. Curve 1 in Fig. 4-29 gives the height y of a catapulted fruitcake versus the angle
 between its velocity vector and its acceleration vector during flight. (a) Which of the lettered points on that curve corresponds to the landing of the fruitcake on the ground? (b) Curve 2 is a similar plot for the same launch speed but for a different launch angle. Does the fruitcake now land farther away or closer to the launch point? between its velocity vector and its acceleration vector during flight. (a) Which of the lettered points on that curve corresponds to the landing of the fruitcake on the ground? (b) Curve 2 is a similar plot for the same launch speed but for a different launch angle. Does the fruitcake now land farther away or closer to the launch point?
| |||||||||||||||
| 9. |
An airplane flying horizontally at a constant speed of 350 km/h over level ground releases a bundle of food supplies. Ignore the effect of the air on the bundle. What are the bundle’s initial (a) vertical and (b) horizontal components of velocity? (c) What is its horizontal component of velocity just before hitting the ground? (d) If the airplane’s speed were, instead, 450 km/h, would the time of fall be longer, shorter, or the same?
|
| 10. |
A ball is shot from ground level over level ground at a certain initial speed. Figure 4-30 gives the range R of the ball versus its launch angle
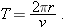 . Rank the three lettered points on the plot according to (a) the total flight time of the ball and (b) the ball’s speed at maximum height, greatest first. . Rank the three lettered points on the plot according to (a) the total flight time of the ball and (b) the ball’s speed at maximum height, greatest first.
| |||||||||||||||
| 11. |
In Fig. 4-31, particle P is in uniform circular motion, centered on the origin of an xy coordinate system. (a) At what values of
 is the vertical component is the vertical component 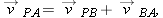 of the position vector greatest in magnitude? (b) At what values of of the position vector greatest in magnitude? (b) At what values of  is the vertical component is the vertical component  of the particle’s velocity greatest in magnitude? (c) At what values of of the particle’s velocity greatest in magnitude? (c) At what values of  is the vertical component is the vertical component 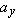 of the particle’s acceleration greatest in magnitude? of the particle’s acceleration greatest in magnitude?
| |||||||||||||||
| 12. |
(a) Is it possible to be accelerating while traveling at constant speed? Is it possible to round a curve with (b) zero acceleration and (c) a constant magnitude of acceleration?
|
| 13. |
Figure 4-32 shows four tracks (either half- or quarter-circles) that can be taken by a train, which moves at a constant speed. Rank the tracks according to the magnitude of a train’s acceleration on the curved portion, greatest first.
| |||||||||||||||
| Copyright © 2008 John Wiley & Sons, Inc. All rights reserved. |