Calculations: Applying the
ax part of Eq.
4-18 to Eq.
4-13, we find the
x component of

to be
Similarly, applying the
ay part of Eq.
4-18 to Eq.
4-14 yields the
y component as
We see that the acceleration does not vary with time (it is a constant) because the time variable
t does not appear in the expression for either acceleration component. Equation
4-17 then yields
which is superimposed on the rabbit’s path in Fig.
4-8.
 |  | |  |  | FIGURE 4-8 | The acceleration 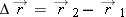 of the rabbit at of the rabbit at  . The rabbit happens to have this same acceleration at all points on its path. . The rabbit happens to have this same acceleration at all points on its path.
|
|  |
|  |
To get the magnitude and angle of

, either we use a vector-capable calculator or we follow Eq. 3-6. For the magnitude we have
For the angle we have
However, this angle, which is the one displayed on a calculator, indicates that

is directed to the right and downward in Fig.
4-8. Yet, we know from the components that

must be directed to the left and upward. To find the other angle that has the same tangent as −35° but is not displayed on a calculator, we add 180°:
This
is consistent with the components of

. Note that

has the same magnitude and direction throughout the rabbit’s run because the acceleration is constant.
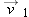 to
to 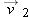 in a time interval
in a time interval  , its average acceleration
, its average acceleration  during
during  is
is
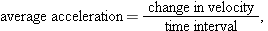
 to zero about some instant, then in the limit
to zero about some instant, then in the limit  approaches the instantaneous acceleration (or acceleration)
approaches the instantaneous acceleration (or acceleration)  at that instant; that is,
at that instant; that is,
 to obtain
to obtain
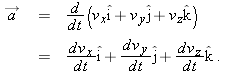
 are
are
 , we differentiate the scalar components of
, we differentiate the scalar components of  .
. and its scalar components for a particle moving in two dimensions. Caution: When an acceleration vector is drawn, as in Fig. 4-7, it does not extend from one position to another. Rather, it shows the direction of acceleration for a particle located at its tail, and its length (representing the acceleration magnitude) can be drawn to any scale.
and its scalar components for a particle moving in two dimensions. Caution: When an acceleration vector is drawn, as in Fig. 4-7, it does not extend from one position to another. Rather, it shows the direction of acceleration for a particle located at its tail, and its length (representing the acceleration magnitude) can be drawn to any scale.
