| 4.6 | Projectile Motion Analyzed |
 |
 |
Now we are ready to analyze projectile motion, horizontally and vertically.
The Horizontal Motion
Because there is
no acceleration in the horizontal direction, the horizontal component
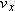
of the projectile’s velocity remains unchanged from its initial value

throughout the motion, as demonstrated in Fig.
4-13. At any time
t, the projectile’s horizontal displacement
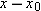
from an initial position
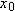
is given by Eq. 2-15 with
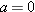
, which we write as
Because
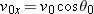
, this becomes
 |  | |  | | Source: Jamie Budge/Liaison/ Getty Images, Inc. |  |
 | FIGURE 4-13 | The vertical component of this skateboarder’s velocity is changing but not the horizontal component, which matches the skateboard’s velocity. As a result, the skateboard stays underneath him, allowing him to land on it.
|
|  |
|  |
The Vertical Motion
The vertical motion is the motion we discussed in Section 2-9 for a particle in free fall. Most important is that the acceleration is constant. Thus, the equations of Table 2-1 apply, provided we substitute −
g for
a and switch to
y notation. Then, for example, Eq. 2-15 becomes
where the initial vertical velocity component

is replaced with the equivalent
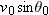
. Similarly, Eqs. 2-11 and 2-16 become
and
As is illustrated in Fig.
4-10 and Eq.
4-23, the vertical velocity component behaves just as for a ball thrown vertically upward. It is directed upward initially, and its magnitude steadily decreases to zero,
which marks the maximum height of the path. The vertical velocity component then reverses direction, and its magnitude becomes larger with time.
The Equation of the Path
We can find the equation of the projectile’s path (its
trajectory) by eliminating time
t between Eqs.
4-21 and
4-22. Solving Eq.
4-21 for
t and substituting into Eq.
4-22, we obtain, after a little rearrangement,
This is the equation of the path shown in Fig.
4-10. In deriving it, for simplicity we let
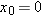
and

in Eqs.
4-21 and
4-22, respectively. Because
g,

, and

are constants, Eq.
4-25 is of the form

, in which
a and
b are constants. This is the equation of a parabola, so the path
is parabolic.
The Horizontal Range
The
horizontal range R of the projectile, as Fig.
4-10 shows, is the
horizontal distance the projectile has traveled when it returns to its initial (launch) height. To find range
R, let us put
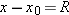
in Eq.
4-21 and
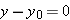
in Eq.
4-22, obtaining
and
Eliminating
t between these two equations yields
Using the identity

(see Appendix E), we obtain
Caution: This equation does
not give the horizontal distance traveled by a projectile when the final height is not the launch height.
Note that
R in Eq.
4-26 has its maximum value when
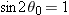
, which corresponds to
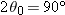
or

.
However, when the launch and landing heights differ, as in shot put, hammer throw, and basketball, a launch angle of 45° does not yield the maximum horizontal distance.
The Effects of the Air
We have assumed that the air through which the projectile moves has no effect on its motion. However, in many situations, the disagreement between our calculations and the actual motion of the projectile can be large because the air resists (opposes) the motion. Figure
4-14, for example, shows two paths for a fly ball that leaves the bat at an angle of 60° with the horizontal and an initial speed of 44.7 m/s. Path I (the baseball player’s fly ball) is a calculated path that approximates normal conditions of play, in air. Path II (the physics professor’s fly ball) is the path the ball would follow in a vacuum.
 |  | |  |  | FIGURE 4-14 | (I) The path of a fly ball calculated by taking air resistance into account. (II) The path the ball would follow in a vacuum, calculated by the methods of this chapter. See Table 4-1 for corresponding data. (Adapted from “The Trajectory of a Fly Ball,” by Peter J. Brancazio, The Physics Teacher, January 1985.)
|
|  |
|  |
 |  |
| | Path I (Air) | Path II (Vacuum) |
Range | 98.5 m | 177 m | Maximum height | 53.0 m | 76.8 m | Time of flight | 6.6 s | 7.9 s |
|
| |
|  |
|  |
 |
 |  | Sample Problem 4-6 Build your skill |  |
|  |  |  |
 |  |  |
(a) What should be the angle  of the pilot’s line of sight to the victim when the release is made?
Calculations: In Fig. 4-15, we see there that  is given by
where x is the horizontal coordinate of the victim (and of the capsule when it hits the water) and h = 500 m. We should be able to find x with Eq. 4-21:
Here we know that 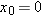 because the origin is placed at the point of release. Because the capsule is released and not shot from the plane, its initial velocity 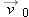 is equal to the plane’s velocity. Thus, we know also that the initial velocity has magnitude 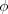 and angle 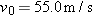 (measured relative to the positive direction of the x axis). However, we do not know the time t the capsule takes to move from the plane to the victim.
To find t, we next consider the vertical motion and specifically Eq. 4-22:
Here the vertical displacement 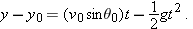 of the capsule is −500 m (the negative value indicates that the capsule moves downward). So,
Solving for t, we find 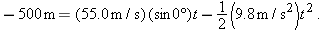 . Using that value in Eq. 4-28 yields
or
Then Eq. 4-27 gives us
|  |  |
|  |  |  |  |
|
 |
 |
(b) As the capsule reaches the water, what is its velocity  in unit-vector notation and in magnitude-angle notation? 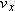 does not change from its initial value does not change from its initial value 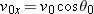 because there is no horizontal acceleration. (3) Component because there is no horizontal acceleration. (3) Component  changes from its initial value changes from its initial value 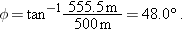 because there is a vertical acceleration. because there is a vertical acceleration.
Calculations: When the capsule reaches the water,
Using Eq. 4-23 and the capsule’s time of fall 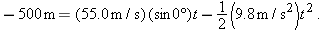 , we also find that when the capsule reaches the water,
Thus, at the water
Using Eq. 3-6 as a guide, we find that the magnitude and the angle of  are
|
 |
|
(b) What is the maximum range of the cannonballs?
Calculations: We have seen that maximum range corresponds to an elevation angle  of 45°. Thus,
As the pirate ship sails away, the two elevation angles at which the ship can be hit draw together, eventually merging at  when the ship is 690 m away. Beyond that distance the ship is safe.
|
 |
 |
 |  |  |
Suppose a baseball batter B hits a high fly ball to the outfield, directly toward an outfielder F and with a launch speed of  and a launch angle of  . During the flight, a line from the outfielder to the ball makes an angle 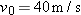 with the ground. Plot elevation angle 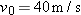 versus time t, assuming that the outfielder is already positioned to catch the ball, is 6.0 m too close to the batter, and is 6.0 m too far away.
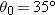 . .
Calculations: The ball can be caught if the outfielder’s distance from the batter is equal to the range R of the ball. Using Eq. 4-26, we find
Figure 4-17a shows a snapshot of the ball in flight when the ball is at height y and horizontal distance x from the batter (who is at the origin). The horizontal distance of the ball from the outfielder is  , and the elevation angle  of the ball in the outfielder’s view is given by  . For the height y, we use Eq. 4-22  , setting  . For the horizontal distance x, we substitute with Eq. 4-21 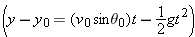 , setting  . Thus, using  and  , we have
 |  | |  |  | FIGURE 4-17 | The elevation angle  for a ball hit toward an outfielder is (a) defined and (b) plotted versus time t. for a ball hit toward an outfielder is (a) defined and (b) plotted versus time t.
|
|  |
|  |
Graphing this function versus t gives the middle plot in Fig. 4-17b. We see that the ball’s angle in the outfielder’s view increases at an almost steady rate throughout the flight.
If the outfielder is 6.0 m too close to the batter, we replace the distance of 153.42 m in Eq. 4-33 with 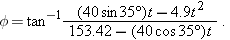 . Regraphing the function gives the “Too close” plot in Fig. 4-17b. Now the elevation angle of the ball rapidly increases toward the end of the flight as the ball soars over the outfielder’s head. If the outfielder is 6.0 m too far away from the batter, we replace the distance of 153.42 m in Eq. 4-33 with 159.42 m. The resulting plot is labeled “Too far” in the figure: The angle first increases and then rapidly decreases. Thus, if a ball is hit directly toward an outfield, the player can tell from the change in the ball’s elevation angle  whether to stay put, run toward the batter, or back away from the batter. |  |  |
|  |  |  |  |
|
 |
 |
 |
 |  | Sample Problem 4-9 Build your skill |  |
|  |  |  |
 |  |  |
At time  , a golf ball is shot from ground level into the air, as indicated in Fig. 4-18a. The angle  between the ball’s direction of travel and the positive direction of the x axis is given in Fig. 4-18b as a function of time t. The ball lands at 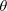 . What is the magnitude  of the ball’s launch velocity, at what height  above the launch level does the ball land, and what is the ball’s direction of travel just as it lands?  |  | |  |  | FIGURE 4-18 | (a) Path of a golf ball shot onto a plateau. (b) The angle  that gives the ball’s direction of motion during the flight is plotted versus time t. that gives the ball’s direction of motion during the flight is plotted versus time t.
|
|  |
|  |
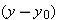 of the ball’s velocity does not change during the flight. (3) The vertical component of the ball’s velocity does not change during the flight. (3) The vertical component  of its velocity does change and is zero when the ball reaches maximum height. (4) The ball’s direction of travel at any time during the flight is at the angle of its velocity vector of its velocity does change and is zero when the ball reaches maximum height. (4) The ball’s direction of travel at any time during the flight is at the angle of its velocity vector  just then. That angle is given by tan just then. That angle is given by tan  , with the velocity components evaluated at that time. , with the velocity components evaluated at that time.
Calculations: When the ball reaches its maximum height, 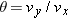 . So, the direction of the velocity  is horizontal, at angle  . From the graph, we see that this condition occurs at  . We also see that the launch angle  (at t = 0) is 80°. Using Eq. 4-23 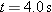 , with t = 4.0 s,  , 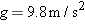 , and 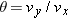 , we find
The ball lands at 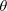 . Using Eq. 4-22  with 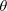 , we obtain
Just as the ball lands, its horizontal velocity 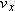 is still  ; substituting for  and  gives us 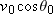 . We find its vertical velocity just then by using Eq. 4-23 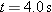 with 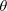 , which yields  . Thus, the angle of the ball’s direction of travel at landing is
|  |  |
|  |  |  |  |
|
 |
 |
 |
| Copyright © 2008 John Wiley & Sons, Inc. All rights reserved. |
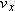 of the projectile’s velocity remains unchanged from its initial value
of the projectile’s velocity remains unchanged from its initial value  throughout the motion, as demonstrated in Fig. 4-13. At any time t, the projectile’s horizontal displacement
throughout the motion, as demonstrated in Fig. 4-13. At any time t, the projectile’s horizontal displacement 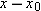 from an initial position
from an initial position 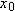 is given by Eq. 2-15 with
is given by Eq. 2-15 with 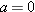 , which we write as
, which we write as
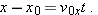
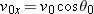 , this becomes
, this becomes
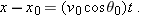
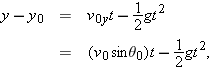
 is replaced with the equivalent
is replaced with the equivalent 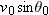 . Similarly, Eqs. 2-11 and 2-16 become
. Similarly, Eqs. 2-11 and 2-16 become
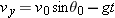

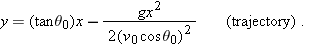
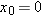 and
and  in Eqs. 4-21 and 4-22, respectively. Because g,
in Eqs. 4-21 and 4-22, respectively. Because g,  , and
, and  are constants, Eq. 4-25 is of the form
are constants, Eq. 4-25 is of the form  , in which a and b are constants. This is the equation of a parabola, so the path is parabolic.
, in which a and b are constants. This is the equation of a parabola, so the path is parabolic.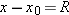 in Eq. 4-21 and
in Eq. 4-21 and 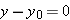 in Eq. 4-22, obtaining
in Eq. 4-22, obtaining
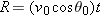
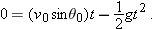
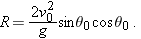
 (see Appendix E), we obtain
(see Appendix E), we obtain
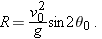


 in unit-vector notation and in magnitude-angle notation?
in unit-vector notation and in magnitude-angle notation?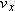 does not change from its initial value
does not change from its initial value 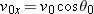 because there is no horizontal acceleration. (3) Component
because there is no horizontal acceleration. (3) Component  changes from its initial value
changes from its initial value 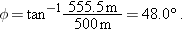 because there is a vertical acceleration.
because there is a vertical acceleration.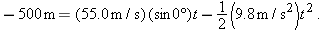 , we also find that when the capsule reaches the water,
, we also find that when the capsule reaches the water,
 are
are
 of 45°. Thus,
of 45°. Thus,
 when the ship is 690 m away. Beyond that distance the ship is safe.
when the ship is 690 m away. Beyond that distance the ship is safe.