| 4.7 | Uniform Circular Motion |
 |
 |
A particle is in uniform circular motion if it travels around a circle or a circular arc at constant (uniform) speed. Although the speed does not vary, the particle is accelerating because velocity changes in direction.
Figure
4-19 shows the relationship between the velocity and acceleration vectors at various stages during uniform circular motion. Both vectors have constant magnitude, but their directions change continuously. The velocity is always directed tangent to the circle in the direction of motion. The acceleration is always directed
radially inward. Because of this, the acceleration associated with uniform circular motion is called a
centripetal (meaning “center seeking”)
acceleration. As we prove next, the magnitude of this acceleration

is
 |
| (4-34) |
 |
where
r is the radius of the circle and
v is the speed of the particle.
 |  | |  |  | FIGURE 4-19 | Velocity and acceleration vectors for uniform circular motion.
|
|  |
|  |
In addition, during this acceleration at constant speed, the particle travels the circumference of the circle (a distance of

) in time
 |
| (4-35) |
 |
T is called the
period of revolution, or simply the
period, of the motion. It is, in general, the time for a particle to go around a closed path exactly once.
Proof of Eq. 4-34
To find the magnitude and direction of the acceleration for uniform circular motion, we consider Fig.
4-20. In Fig.
4-20a, particle
p moves at constant speed
v around a circle of radius
r. At the instant shown,
p has coordinates

and
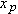
.
 |  | |  |  | FIGURE 4-20 | Particle p moves in counterclockwise uniform circular motion. (a) Its position and velocity  at a certain instant. (b) Velocity at a certain instant. (b) Velocity  . (c) Acceleration . (c) Acceleration  . .
|
|  |
|  |
Recall from Section
4-3 that the velocity

of a moving particle is always tangent to the particle’s path at the particle’s position. In Fig.
4-20a, that means

is perpendicular to a radius
r drawn to the particle’s position. Then the angle

that

makes with a vertical at
p equals the angle
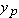
that radius
r makes with the
x axis.
The scalar components of

are shown in Fig.
4-20b. With them, we can write the velocity

as
Now, using the right triangle in Fig.
4-20a, we can replace
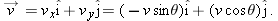
with
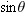
and
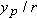
with
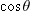
to write
To find the acceleration

of particle
p, we must take the time derivative of this equation. Noting that speed
v and radius
r do not change with time, we obtain
Now note that the rate
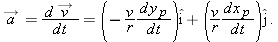
at which
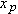
changes is equal to the velocity component

. Similarly,
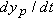
, and, again from Fig.
4-20b, we see that
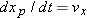
and
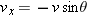
. Making these substitutions in Eq.
4-38, we find
This vector and its components are shown in Fig.
4-20c. Following Eq. 3-6, we find
as we wanted to prove. To orient

, we find the angle
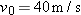
shown in Fig.
4-20c:
Thus,
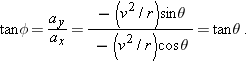
, which means that

is directed along the radius
r of Fig.
4-20a, toward the circle’s center, as we wanted to prove.
 |
 |  |  |
“Top gun” pilots have long worried about taking a turn too tightly. As a pilot’s body undergoes centripetal acceleration, with the head toward the center of curvature, the blood pressure in the brain decreases, leading to loss of brain function.
There are several warning signs. When the centripetal acceleration is 2g or 3g, the pilot feels heavy. At about 4g, the pilot’s vision switches to black and white and narrows to “tunnel vision.” If that acceleration is sustained or increased, vision ceases and, soon after, the pilot is unconscious—a condition known as g-LOC for “g-induced loss of consciousness.”
What is the magnitude of the acceleration, in g units, of a pilot whose aircraft enters a horizontal circular turn with a velocity of 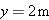 and 24.0 s later leaves the turn with a velocity of 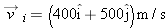 ?
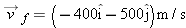 , where R is the circle’s radius. Also, the time required to complete a full circle is the period given by Eq. 4-35 , where R is the circle’s radius. Also, the time required to complete a full circle is the period given by Eq. 4-35  . .
Calculations: Because we do not know radius R, let’s solve Eq. 4-35 for R and substitute into Eq. 4-34. We find
Speed v here is the (constant) magnitude of the velocity during the turning. Let’s substitute the components of the initial velocity into Eq. 3-6:
To find the period T of the motion, first note that the final velocity is the reverse of the initial velocity. This means the aircraft leaves on the opposite side of the circle from the initial point and must have completed half a circle in the given 24.0 s. Thus a full circle would have taken 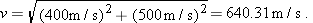 . Substituting these values into our equation for a, we find
|  |  |
|  |  |  |  |
|
 |
 |
 |
| Copyright © 2008 John Wiley & Sons, Inc. All rights reserved. |
 is
is
 ) in time
) in time
 and
and 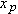 .
. of a moving particle is always tangent to the particle’s path at the particle’s position. In Fig. 4-20a, that means
of a moving particle is always tangent to the particle’s path at the particle’s position. In Fig. 4-20a, that means  is perpendicular to a radius r drawn to the particle’s position. Then the angle
is perpendicular to a radius r drawn to the particle’s position. Then the angle  that
that  makes with a vertical at p equals the angle
makes with a vertical at p equals the angle 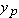 that radius r makes with the x axis.
that radius r makes with the x axis. are shown in Fig. 4-20b. With them, we can write the velocity
are shown in Fig. 4-20b. With them, we can write the velocity  as
as
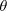
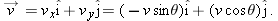 with
with 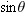 and
and 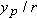 with
with 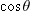 to write
to write
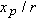
 of particle p, we must take the time derivative of this equation. Noting that speed v and radius r do not change with time, we obtain
of particle p, we must take the time derivative of this equation. Noting that speed v and radius r do not change with time, we obtain
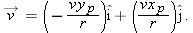
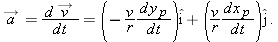 at which
at which 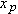 changes is equal to the velocity component
changes is equal to the velocity component  . Similarly,
. Similarly, 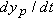 , and, again from Fig. 4-20b, we see that
, and, again from Fig. 4-20b, we see that 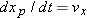 and
and 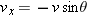 . Making these substitutions in Eq. 4-38, we find
. Making these substitutions in Eq. 4-38, we find
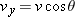
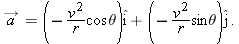
 , we find the angle
, we find the angle 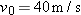 shown in Fig. 4-20c:
shown in Fig. 4-20c:
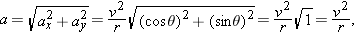
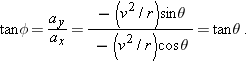 , which means that
, which means that  is directed along the radius r of Fig. 4-20a, toward the circle’s center, as we wanted to prove.
is directed along the radius r of Fig. 4-20a, toward the circle’s center, as we wanted to prove.
