| 4.8 | Relative Motion in One Dimension |
 |
 |
Suppose you see a duck flying north at 30 km/h.To another duck flying alongside, the first duck seems to be stationary. In other words, the velocity of a particle depends on the reference frame of whoever is observing or measuring the velocity. For our purposes, a reference frame is the physical object to which we attach our coordinate system. In everyday life, that object is the ground. For example, the speed listed on a speeding ticket is always measured relative to the ground. The speed relative to the police officer would be different if the officer were moving while making the speed measurement.
Suppose that Alex (at the origin of frame
A in Fig.
4-21) is parked by the side of a highway, watching car
P (the “particle”) speed past. Barbara (at the origin of frame
B) is driving along the highway at constant speed and is also watching car
P. Suppose that they both measure the position of the car at a given moment. From Fig.
4-21 we see that
The equation is read: “The coordinate

of
P as measured by
A is equal to the coordinate
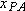
of
P as measured by
B plus the coordinate

of
B as measured by
A.” Note how this reading is supported by the sequence of the subscripts.
 |  | |  |  | FIGURE 4-21 | Alex (frame A) and Barbara (frame B) watch car P, as both B and P move at different velocities along the common x axis of the two frames. At the instant shown,  is the coordinate of B in the A frame. Also, P is at coordinate is the coordinate of B in the A frame. Also, P is at coordinate  in the B frame and coordinate in the B frame and coordinate 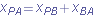 in the A frame. in the A frame.
|
|  |
|  |
Taking the time derivative of Eq.
4-40, we obtain
Thus, the velocity components are related by
 |
| (4-41) |
 |
This equation is read: “The velocity

of
P as measured by
A is equal to the velocity

of
P as measured by
B plus the velocity

of
B as measured by
A.” The term

is the velocity of frame
B relative to frame
A.
Here we consider only frames that move at constant velocity relative to each other. In our example, this means that Barbara (frame
B) drives always at constant velocity

relative to Alex (frame
A). Car
P (the moving particle), however, can change speed and direction (that is, it can accelerate).
To relate an acceleration of
P as measured by Barbara and by Alex, we take the time derivative of Eq.
4-41:
Because

is constant, the last term is zero and we have
 |
| (4-42) |
 |
In other words,
(b) If car P brakes to a stop relative to Alex (and thus relative to the ground) in time 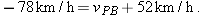 at constant acceleration, what is its acceleration 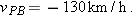 relative to Alex? 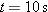 to relate the acceleration to the initial and final velocities of P. to relate the acceleration to the initial and final velocities of P.
Calculation: The initial velocity of P relative to Alex is 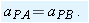 and the final velocity is 0. Thus,
|
 |
(c) What is the acceleration 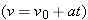 of car P relative to Barbara during the braking?
Calculation: We know the initial velocity of P relative to Barbara from part (a) 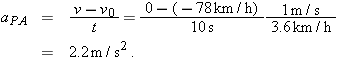 . The final velocity of P relative to Barbara is −52 km/h (this is the velocity of the stopped car relative to the moving Barbara). Thus,
Comment: We should have foreseen this result: Because Alex and Barbara have a constant relative velocity, they must measure the same acceleration for the car.
|
 |
 |
| Copyright © 2008 John Wiley & Sons, Inc. All rights reserved. |
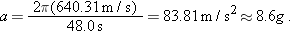
 of P as measured by A is equal to the coordinate
of P as measured by A is equal to the coordinate 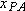 of P as measured by B plus the coordinate
of P as measured by B plus the coordinate  of B as measured by A.” Note how this reading is supported by the sequence of the subscripts.
of B as measured by A.” Note how this reading is supported by the sequence of the subscripts.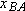
 of P as measured by A is equal to the velocity
of P as measured by A is equal to the velocity  of P as measured by B plus the velocity
of P as measured by B plus the velocity  of B as measured by A.” The term
of B as measured by A.” The term  is the velocity of frame B relative to frame A.
is the velocity of frame B relative to frame A. relative to Alex (frame A). Car P (the moving particle), however, can change speed and direction (that is, it can accelerate).
relative to Alex (frame A). Car P (the moving particle), however, can change speed and direction (that is, it can accelerate).
 is constant, the last term is zero and we have
is constant, the last term is zero and we have
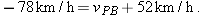 at constant acceleration, what is its acceleration
at constant acceleration, what is its acceleration 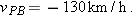 relative to Alex?
relative to Alex?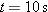 to relate the acceleration to the initial and final velocities of P.
to relate the acceleration to the initial and final velocities of P.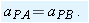 and the final velocity is 0. Thus,
and the final velocity is 0. Thus,
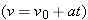 of car P relative to Barbara during the braking?
of car P relative to Barbara during the braking?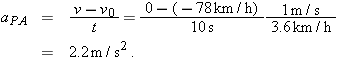 . The final velocity of P relative to Barbara is −52 km/h (this is the velocity of the stopped car relative to the moving Barbara). Thus,
. The final velocity of P relative to Barbara is −52 km/h (this is the velocity of the stopped car relative to the moving Barbara). Thus,