|
Describing the 3D World: Vectors |
 |
Physical phenomena take place in the 3D world around us. In order to be able to make quantitative predictions and give detailed,
quantitative explanations, we need tools for describing precisely the positions and velocities of objects in 3D, and the changes
in position and velocity due to interactions. These tools are mathematical entities called 3D “vectors.”
3D Coordinates
We will use a 3D coordinate system to specify positions in space and other vector quantities. Usually we will orient the axes
of the coordinate system as shown in Figure 1.10: +
x axis to the right, +
y axis upward, and +
z axis coming out of the page, toward you. This is a “right-handed” coordinate system: if you hold the thumb, first, and second
fingers of your right hand perpendicular to each other, and align your thumb with the
x axis and your first finger with the
y axis, your second finger points along the
z axis. (In some math and physics textbook discussions of 3D coordinate systems, the
x axis points out, the
y axis points to the right, and the
z axis points up, but we will also use a 2D coordinate system with
y up, so it makes sense always to have the
y axis point up.)
 |
 |
|
|
 |
| Figure 1.10 |
Right-handed 3D coordinate system.
|
|
 |
|
 |
Basic Properties of Vectors: Magnitude and Direction
A vector is a quantity that has a magnitude and a direction. For example, the velocity of a baseball is a vector quantity.
The magnitude of the baseball's velocity is the speed of the baseball—for example, 20 meters/second. The direction of the
baseball's velocity is the direction of its motion at a particular instant—for example, “up” or “to the right” or “west” or
“in the +
y direction.” A symbol denoting a vector is written with an arrow over it:
Position
A position in space can also be considered to be a vector, called a
position vector, pointing from an origin to that location. Figure 1.11 shows a position vector that might represent your final position if you started at the origin and walked 4 meters along the
x axis, then 2 meters parallel to the
z axis, then climbed a ladder so you were 3 meters above the ground. Your new position relative to the origin is a vector that
can be written like this:
In three dimensions a vector is a triple of numbers
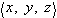
. Quantities like the position of an object and the velocity of an object can be represented as vectors:
 |
 |
|
|
 |
| Figure 1.11 |
A position vector 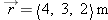 and its x, y, and z components. and its x, y, and z components.
|
|
 |
|
 |
Components of a Vector
Each of the numbers in the triple is referred to as a
component of the vector. The
x component of the vector
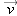
is the number
vx. The
z component of the vector
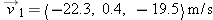
is
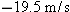
. A component such as
vx is not a vector, since it is only one number.
Drawing Vectors
In Figure 1.11 we represented your position vector relative to the origin graphically by an arrow whose tail is at the origin and whose
arrowhead is at your position. The length of the arrow represents the distance from the origin, and the direction of the arrow
represents the direction of the vector, which is the direction of a direct path from the initial position to the final position
(the “displacement”; by walking and climbing you “displaced” yourself from the origin to your final position).
Vectors and Scalars
A quantity that is represented by a single number is called a
scalar. A scalar quantity does not have a direction. Examples include the mass of an object, such as 5 kg, or the temperature, such
as −20°C. Vectors and scalars are very different entities; a vector can never be equal to a scalar, and a scalar cannot be
added to a vector. Scalars can be positive or negative:
Although a component of a vector such as
vx is not a vector, it's not a scalar either, despite being only one number. An important property of a true scalar is that
its value doesn't change if we orient the
xyz coordinate axes differently. Rotating the axes doesn't change an object's mass, or the temperature, but it does change what
we mean by the
x component of the velocity since the
x axis now points in a different direction.
| 1.X.6 |
How many numbers are needed to specify a 3D position vector?
Answer:
three
|
|
 |
 |
 |
| 1.X.7 |
How many numbers are needed to specify a scalar?
Answer:
one
|
|
 |
 |
 |
|
|
|
|
Magnitude of a Vector
The magnitude of a vector can be calculated by taking the square root of the sum of the squares of its components (see Figure
1.15).
The magnitude of a vector is a true scalar, because its value doesn't change if you rotate the coordinate axes. Rotating the
axes changes the individual components, but the length of the arrow representing the vector doesn't change.
Can a Vector Be Positive or Negative?
None of these descriptions is appropriate. The x component of this vector is positive, the y component is zero, and the z component is negative. Vectors aren't positive, or negative, or zero. Their components can be positive or negative or zero,
but these words just don't mean anything when used with the vector as a whole.
On the other hand, the
magnitude of a vector such as

is always positive.
| 1.X.8 |
If 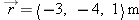 , find  .
Answer:
5.10 m
|
|
 |
 |
 |
| 1.X.9 |
Can the magnitude of a vector be a negative number?
Answer:
no
|
|
 |
 |
 |
|
|
|
|
Mathematical Operations Involving Vectors
Although the algebra of vectors is similar to the scalar algebra with which you are very familiar, it is not identical. There
are some algebraic operations that cannot be performed on vectors.
Algebraic operations that
are legal for vectors include the following operations, which we will discuss in this chapter:
In later chapters we will also see that there are two more ways of combining two vectors:
 |
|
The vector dot product, whose result is a scalar
|
 |
|
The vector cross product, whose result is a vector
|
|
Operations That Are Not Legal for Vectors
Although vector algebra is similar to the ordinary scalar algebra you have used up to now, there are certain operations that
are not legal (and not meaningful) for vectors:
 |
|
A vector cannot be set equal to a scalar.
|
 |
|
A vector cannot be added to or subtracted from a scalar.
|
 |
|
A vector cannot occur in the denominator of an expression. (Although you can't divide by a vector, note that you can legally
divide by the magnitude of a vector, which is a scalar.)
|
|
| 1.X.10 |
The vector 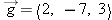 and the scalar h = −2. What is 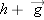 ?
 |
|
(a)
|
 0, −9, 1  |
 |
|
(b)
|
 4, −5, 5  |
 |
|
(c)
|
 4, 9, 5  |
 |
|
(d)
|
This is a meaningless expression.
|
|
Answer:
d
|
|
 |
 |
 |
| 1.X.11 |
Is 4/  6, −7, 4  a meaningful expression? If so, what is its value?
Answer:
no
|
|
 |
 |
 |
|
|
|
|
Multiplying a Vector by a Scalar
| 1.X.12 |
The vector 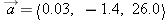 and the scalar f = −3.0. What is 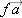 ?
Answer:
 −0.09, 4.2, −78.0  |
|
 |
 |
 |
| 1.X.13 |
If 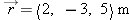 , what is 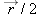 ?
Answer:
 1, −1.5, 2.5  |
|
 |
 |
 |
|
|
|
|
Magnitude of a Scalar
You may wonder how to find the magnitude of a quantity like
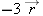
, which involves the product of a scalar and a vector. This expression can be factored:
The magnitude of a scalar is its absolute value, so:
| 1.X.14 |
If 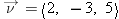 m/s, what is the magnitude of 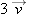 ?
Answer:
 6, −9, 15  m/s
|
|
 |
 |
 |
| 1.X.15 |
How does the magnitude of the vector 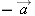 compare to the magnitude of the vector 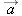 ?
Answer:
They are the same.
|
|
 |
 |
 |
|
|
|
|
Direction of a Vector: Unit Vectors
One way to describe the direction of a vector is by specifying a
unit vector. A unit vector is a vector of magnitude 1, pointing in some direction. A unit vector is written with a “hat” (caret) over
it instead of an arrow. The unit vector
â is called “a-hat.”
The magnitude of
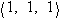
is
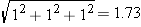
, so this is not a unit vector.
The vector
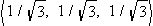
is a unit vector, since its magnitude is 1:
Note that every component of a unit vector must be less than or equal to 1.
In our 3D Cartesian coordinate system, there are three special unit vectors, oriented along the three axes. They are called
i-hat, j-hat, and k-hat, and they point along the
x,
y, and
z axes, respectively (Figure 1.17):
 |
 |
|
|
 |
| Figure 1.17 |
The unit vectors î, ĵ, 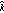 . .
|
|
 |
|
 |
One way to express a vector is in terms of these special unit vectors:
We will usually use the
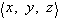
form rather than the
îĵ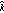
form in this book, because the familiar
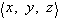
notation, used in many calculus textbooks, emphasizes that a vector is a single entity.
Calculating Unit Vectors
| 1.X.16 |
What is the unit vector in the direction of  0, 6, 0  ?
Answer:
 0, 1, 0  |
|
 |
 |
 |
| 1.X.17 |
What is the unit vector â in the direction of 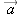 , where 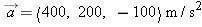 ?
Answer:
 0.873, 0.436, −0.218  |
|
 |
 |
 |
|
|
|
|
Equality of Vectors
| 1.X.18 |
If 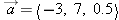 , and 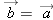 , what is the y component of 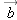 ?
Answer:
7
|
|
 |
 |
 |
|
|
|
|
Vector Addition
Warning: Don't Add Magnitudes!
The magnitude of a vector is
not in general equal to the sum of the magnitudes of the two original vectors! For example, the magnitude of the vector

3, 0, 0

is 3, and the magnitude of the vector

−2, 0, 0

is 2, but the magnitude of the vector (

3, 0, 0

+

−2, 0, 0

) is 1, not 5!
Adding Vectors Graphically: Tip to Tail
The sum of two vectors has a geometric interpretation. In Figure 1.20 you first walk along displacement vector
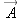
, followed by walking along displacement vector
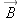
. What is your net displacement vector
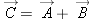
? The
x component
Cx of your net displacement is the sum of
Ax and
Bx. Similarly, the
y component
Cy of your net displacement is the sum of
Ay and
By.
 |
 |
|
|
 |
| Figure 1.20 |
The procedure for adding two vectors graphically: draw vectors tip to tail. To add 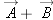 graphically, move graphically, move 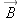 so the tail of so the tail of 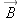 is at the tip of is at the tip of 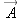 , then draw a new arrow starting at the tail of , then draw a new arrow starting at the tail of 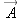 and ending at the tip of and ending at the tip of 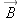 . .
|
|
 |
|
 |
| 1.X.20 |
If 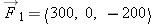 and 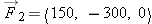 , what is the magnitude of 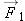 ? What is the magnitude of 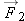 ? What is the magnitude of 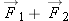 ? What is the magnitude of 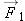 plus the magnitude of 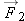 ? Is  ?
Answer:
361, 335, 577, 696, no
|
|
 |
 |
 |
| 1.X.21 |
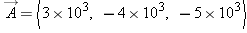 and 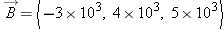 . Calculate the following:
Answer:
|
|
 |
 |
 |
|
|
|
|
Vector Subtraction
The difference of two vectors will be very important in this and subsequent chapters. To subtract one vector from another,
we subtract the components of the second vector from the components of the first:
| 1.X.22 |
If 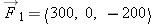 and 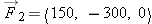 , what is the sum 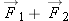 ? What is the difference 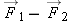 ? What is 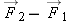 ?
Answer:
|
|
 |
 |
 |
|
|
|
|
Subtracting Vectors Graphically: Tail to Tail
To subtract one vector
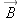
from another vector
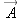
graphically:
 |
|
|
Draw the first vector 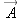 .
|
 |
|
|
Move the second vector 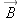 (without rotating it) so its tail is located at the tail of the first vector.
|
 |
|
|
Draw a new vector from the tip of vector 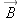 to the tip of vector 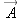 .
|
|
Note that you can check this algebraically and graphically. As shown in Figure 1.21, since the tail of
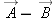
is located at the tip of
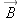
, then the vector
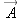
should be the sum of
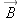
and
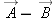
, as indeed it is:
 |
 |
|
|
 |
| Figure 1.21 |
The procedure for subtracting vectors graphically: draw vectors tail to tail; draw a new vector from the tip of the second
vector to the tip of the first vector.
|
|
 |
|
 |
Commutativity and Associativity
Vector addition is commutative:
Vector subtraction is
not commutative:
The associative property holds for vector addition and subtraction:
The Zero Vector
It is convenient to have a compact notation for a vector whose components are all zero. We will use the symbol
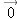
to denote a zero vector, in order to distinguish it from a scalar quantity that has the value 0.
For example, the sum of two vectors
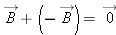
.
Change in a Quantity: The Greek Letter Δ
Frequently we will want to calculate the change in a quantity. For example, we may want to know the change in a moving object's
position or the change in its velocity during some time interval. The Greek letter Δ (capital delta suggesting “d for difference”)
is used to denote the change in a quantity (either a scalar or a vector).
We use the subscript
i to denote an
initial value of a quantity, and the subscript
f to denote the
final value of a quantity. If a vector
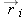
denotes the initial position of an object relative to the origin (its position at the beginning of a time interval), and
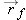
denotes the final position of the object, then
 |
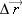 means “change of 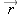 ” or 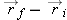 (displacement)
|
 |
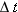 means “change of t” or t f − t i (time interval)
|
|
The symbol Δ (delta) always means “final minus initial, ” not “initial minus final.” For example, when a child's height changes
from 1.1 m to 1.2 m, the change is Δ
y = +0.1 m, a positive number. If your bank account dropped from $150 to $130, what was the change in your balance? Δ (bank
account) = −20 dollars.
Relative Position Vectors
| 1.X.24 |
At 10:00 AM you are at location  −3, 2, 5  m. By 10:02 AM you have walked to location  6, 4, 25  m.
 |
|
(a)
|
What is 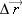 , the change in your position?
|
 |
|
(b)
|
What is Δt, the time interval during which your position changed?
|
|
Answer:
 |
|
(a)
|
 9, 2, 20  m,
|
 |
|
(b)
|
120 s
|
|
|
|
 |
 |
 |
| 1.X.25 |
A snail is initially at location 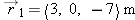 . At a later time the snail has crawled to location 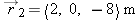 . What is 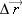 , the change in the snail's position?
Answer:
|
|
 |
 |
 |
|
|
|
|
Unit Vectors and Angles
Suppose that a taut string is at an angle
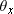
to the +
x axis, and we need a unit vector in the direction of the string. Figure 1.24 shows a unit vector
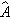
pointing along the string. What is the
x component of this unit vector? Consider the triangle whose base is
Ax and whose hypotenuse is
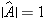
. From the definition of the cosine of an angle we have this:
In Figure 1.24 the angle
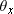
is shown in the first quadrant (
θx less than 90°), but this works for larger angles as well. For example, in Figure 1.25 the angle from the +
x axis to a unit vector
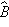
is in the second quadrant (
θx greater than 90°) and cos
θx is negative, which corresponds to
Bx being negative.
 |
 |
|
|
 |
| Figure 1.24 |
A unit vector whose direction is at a known angle from the +x axis.
|
|
 |
|
 |
 |
 |
|
|
 |
| Figure 1.25 |
A unit vector in the second quadrant from the +x axis.
|
|
 |
|
 |
What is true for
x is also true for
y and
z. Figure 1.26 shows a 3D unit vector
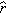
and indicates the angles between the unit vector and the
x,
y, and
z axes. Evidently we can write
These three cosines of the angles between a vector (or unit vector) and the coordinate axes are called the “direction cosines”
of the vector. The cosine function is never greater than 1, just as no component of a unit vector can be greater than 1.
 |
 |
|
|
 |
| Figure 1.26 |
A 3D unit vector and its angles to the x, y, and z axes.
|
|
 |
|
 |
A common special case is that of a unit vector lying in the
xy plane, with zero
z component (Figure 1.27). In this case
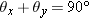
, so that
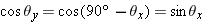
, therefore you can express the cosine of
θy as the sine of
θx, which is often convenient. However, in the general 3D case shown in Figure 1.26 there is no such simple relationship among the direction angles or among their cosines.
 |
 |
|
|
 |
| Figure 1.27 |
If a vector lies in the xy plane, 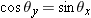 . .
|
|
 |
|
 |
 |
 |
 |
Finding a Unit Vector from Angles |
|
 |
 |
 |
 |
To find a unit vector if angles are given:
 |
|
|
Redraw the vector of interest with its tail at the origin, and determine the angles between this vector and the axes.
|
 |
|
|
Imagine the vector  1, 0, 0  , which lies on the + x axis. θx is the angle through which you would rotate the vector  1, 0, 0  until its direction matched that of your vector. θx is positive, and 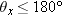 .
|
 |
|
|
θy is the angle through which you would rotate the vector  0, 1, 0  until its direction matched that of your vector. θy is positive, and 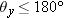 .
|
 |
|
|
θz is the angle through which you would rotate the vector  0, 0, 1  until its direction matched that of your vector. θz is positive, and 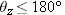 .
|
|
|
 |
 |
|
 |
 |
 |
 |
 |
 |
Further Discussion
You may have noticed that the
y component of the unit vector can also be calculated as sin 70° = 0.940, and it is often useful to recognize that a vector
component can be obtained using sine instead of cosine. There is, however, some advantage always to calculate in terms of
direction cosines. This is a method that always works, including in 3D, and that avoids having to decide whether to use a
sine or a cosine. Just use the cosine of the angle from the relevant positive axis to the vector.
 |
 |
 |
 |
From Unit Vector to Angles
A vector 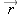 points from the origin to the location  −600, 0, 300  m. What is the angle that this vector makes to the x axis? To the y axis? To the z axis?
|
 |
 |
|
 |
 |
|
|
But we also know that 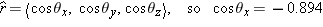 , and the arccosine gives θx = 153.4°. Similarly,
|
|
|
 |
|
|
Further Discussion
Looking down on the
xz plane in Figure 1.30, you can see that the difference between
θx = 153.4° and
θz = 63.4° is 90°, as it should be.
 |
 |
|
|
 |
| Figure 1.30 |
Look down on the xz plane. The difference in the two angles is 90°, as it should be.
|
|
 |
|
 |
 |
| Copyright © 2011 John Wiley & Sons, Inc. All rights reserved. |
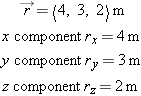
 . Quantities like the position of an object and the velocity of an object can be represented as vectors:
. Quantities like the position of an object and the velocity of an object can be represented as vectors:

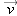 is the number vx. The z component of the vector
is the number vx. The z component of the vector 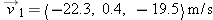 is
is 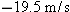 . A component such as vx is not a vector, since it is only one number.
. A component such as vx is not a vector, since it is only one number.
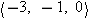 .
.
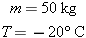
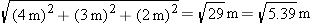
 of the position vector
of the position vector 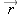 is
is
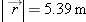
 , or simply by writing the symbol for the vector without the little arrow above it, r.
, or simply by writing the symbol for the vector without the little arrow above it, r.


 is always positive.
is always positive.
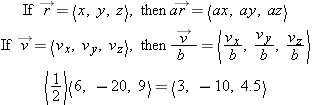
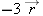 , which involves the product of a scalar and a vector. This expression can be factored:
, which involves the product of a scalar and a vector. This expression can be factored:
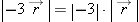
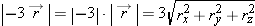
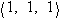 is
is 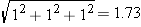 , so this is not a unit vector.
, so this is not a unit vector.
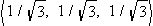 is a unit vector, since its magnitude is 1:
is a unit vector, since its magnitude is 1:
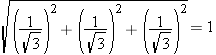
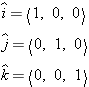
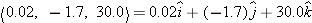
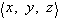 form rather than the îĵ
form rather than the îĵ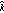 form in this book, because the familiar
form in this book, because the familiar 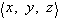 notation, used in many calculus textbooks, emphasizes that a vector is a single entity.
notation, used in many calculus textbooks, emphasizes that a vector is a single entity.

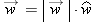
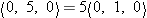






 3, 0, 0
3, 0, 0 is 3, and the magnitude of the vector
is 3, and the magnitude of the vector  −2, 0, 0
−2, 0, 0 is 2, but the magnitude of the vector (
is 2, but the magnitude of the vector ( 3, 0, 0
3, 0, 0 +
+  −2, 0, 0
−2, 0, 0 ) is 1, not 5!
) is 1, not 5!
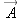 , followed by walking along displacement vector
, followed by walking along displacement vector 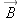 . What is your net displacement vector
. What is your net displacement vector 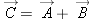 ? The x component Cx of your net displacement is the sum of Ax and Bx. Similarly, the y component Cy of your net displacement is the sum of Ay and By.
? The x component Cx of your net displacement is the sum of Ax and Bx. Similarly, the y component Cy of your net displacement is the sum of Ay and By.


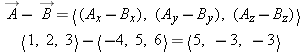
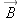 from another vector
from another vector 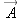 graphically:
graphically:
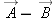 is located at the tip of
is located at the tip of 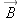 , then the vector
, then the vector 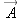 should be the sum of
should be the sum of 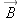 and
and 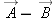 , as indeed it is:
, as indeed it is:
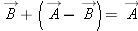
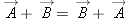
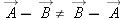
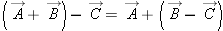
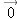 to denote a zero vector, in order to distinguish it from a scalar quantity that has the value 0.
to denote a zero vector, in order to distinguish it from a scalar quantity that has the value 0.
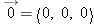
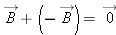 .
.
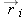 denotes the initial position of an object relative to the origin (its position at the beginning of a time interval), and
denotes the initial position of an object relative to the origin (its position at the beginning of a time interval), and
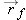 denotes the final position of the object, then
denotes the final position of the object, then
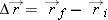
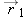 and object 2 is at location
and object 2 is at location 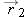 . We want the components of a vector that points from object 1 to object 2. This is the vector obtained by subtraction:
. We want the components of a vector that points from object 1 to object 2. This is the vector obtained by subtraction: 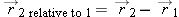 . Note that the form is always “final” minus “initial” in these calculations.
. Note that the form is always “final” minus “initial” in these calculations.
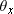 to the +x axis, and we need a unit vector in the direction of the string. Figure 1.24 shows a unit vector
to the +x axis, and we need a unit vector in the direction of the string. Figure 1.24 shows a unit vector 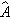 pointing along the string. What is the x component of this unit vector? Consider the triangle whose base is Ax and whose hypotenuse is
pointing along the string. What is the x component of this unit vector? Consider the triangle whose base is Ax and whose hypotenuse is 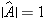 . From the definition of the cosine of an angle we have this:
. From the definition of the cosine of an angle we have this:
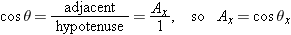
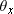 is shown in the first quadrant (θx less than 90°), but this works for larger angles as well. For example, in Figure 1.25 the angle from the +x axis to a unit vector
is shown in the first quadrant (θx less than 90°), but this works for larger angles as well. For example, in Figure 1.25 the angle from the +x axis to a unit vector 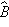 is in the second quadrant (θx greater than 90°) and cosθx is negative, which corresponds to Bx being negative.
is in the second quadrant (θx greater than 90°) and cosθx is negative, which corresponds to Bx being negative.
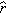 and indicates the angles between the unit vector and the x, y, and z axes. Evidently we can write
and indicates the angles between the unit vector and the x, y, and z axes. Evidently we can write
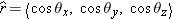
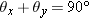 , so that
, so that 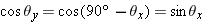 , therefore you can express the cosine of θy as the sine of θx, which is often convenient. However, in the general 3D case shown in Figure 1.26 there is no such simple relationship among the direction angles or among their cosines.
, therefore you can express the cosine of θy as the sine of θx, which is often convenient. However, in the general 3D case shown in Figure 1.26 there is no such simple relationship among the direction angles or among their cosines.

