|
Potential Difference in a Uniform Field |
 |
When working with electric forces, we found it quite useful to be able to calculate the electric field at a particular location
without having to worry about what kind of charged particle might come along to be affected by this field. When we know the
electric field
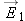
at a location, to find the electric force on whatever particle happens to be at that location, we simply multiply
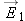
by the charge of the particle,
q2:
Likewise, when calculating changes in potential energy of a system, it would be useful to find a quantity that is independent
of the charge of the particle that might move through a region. Then we could simply multiply this quantity by the charge
of whatever particle happened to move through the region, to get the change in potential energy of the system. We would like
to be able to write:
In the two cases discussed in the previous section (proton or electron moving in a uniform field), many things about the system
were the same: the capacitor, the electric field in the region, and the path taken by the particle between the initial location
A and final location
B. Let's rewrite the change in electric potential energy in each case as the product of the charge of the displaced particle
and another quantity:
The quantity that is the same in both cases is (−
ExΔ
x). This quantity is called the “difference of the electric potential between locations
A and
B,” and is given the symbol Δ
V.
Like energy, electric potential is a scalar quantity. The dimensions of a difference in electric potential Δ
V are joules/coulomb, or “difference of energy per unit charge.” This is such an important quantity that it has its own name:
Units of Field and of Energy
Note that since ΔV = −(ExΔx + EyΔy + EzΔz), and the units of ΔV are volts, then the units of electric field must be volts per meter. This is in fact equivalent to newtons per coulomb, and
can be used interchangeably.
We can also now understand the origin of the energy unit “electron volt,” or eV. One eV is equal to 1.6 × 10
−19J. If an electron moves through a potential difference of one volt, there is a change in the electric potential energy whose
magnitude is
The electron volt is a convenient unit for measuring energies of atomic processes in physics and chemistry. Note that an electron
volt is a unit of energy, not potential (potential is measured in volts, not electron volts).
Path Not Parallel to Electric Field
Note that this quantity can be positive or negative, since each component of the electric field can be positive or negative,
and each component of the displacement can also be positive or negative.
The quantity
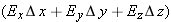
can be written as the “dot product” of the electric field and the displacement vector
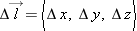
:
 |
 |
 |
Potential Difference in a Uniform Field |
|
 |
 |
|
 |
 |
 |
 |
 |
 |
 |
 |
 |
Potential and Potential Energy
Figure 17.7 shows two locations, A and B, in a region of uniform electric field. For a path starting at A and going to B, calculate the following quantities:
 |
|
(a)
|
the difference in electric potential,
|
 |
|
(b)
|
the potential energy change for the system when a proton moves along this path, and
|
 |
|
(c)
|
|
|
|
 |
 |
|
 |
 |
|
|
 |
|
(a)
|
Potential difference:
Initial location: A
|
 |
|
(b)
|
|
 |
|
(c)
|
|
|
|
|
|
 |
|
|
| 17.X.5 |
For a path starting at B and going to A (Figure 17.9), calculate
 |
|
(a)
|
the change in electric potential,
|
 |
|
(b)
|
the potential energy change for the system when a proton moves from B to A, and
|
 |
|
(c)
|
|
|
Answer:
 |
|
(a)
|
300 V;
|
 |
|
(b)
|
4.8 × 10−17 J;
|
 |
|
(c)
|
−4.8 × 10−17 J
|
|
|
|
 |
 |
 |
| 17.X.6 |
For a path starting at B and going to C (Figure 17.9), calculate
 |
|
(a)
|
the change in electric potential,
|
 |
|
(b)
|
the potential energy change for the system when a proton moves from B to C, and
|
 |
|
(c)
|
the potential energy change for the system when an electron moves from B to C.
|
|
Answer:
|
|
 |
 |
 |
|
|
|
|
Calculating Field from Potential Difference
We have just seen how to calculate potential difference Δ
V from the electric field
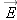
. Conversely, we can calculate electric field from potential difference. Moving in the
x direction, we have Δ
V = −
ExΔ
x, or
Gradient of Potential
In the limit of very short distance,
Ex is given by a derivative:
More technically, the gradient should be written using “partial derivatives,” like this:
The meaning of ∂V/∂x is simply “take the derivative of V with respect to x while holding y and z constant.” The fact that Ex = −∂V/∂x is closely related to the fact that (as we saw in Chapter 6 on energy) Fx = −∂U/∂x, because E = F/q and V = U/q.
The gradient is often written in the form
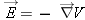
, where the inverted delta (“nabla”) represents taking the
x,
y, and
z partial derivatives of the potential to find the
x,
y, and
z components of the electric field.
| 17.X.7 |
Suppose that the potential difference between location 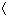 2.00, 3.50, 4.00 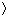 m and location  2.00, 3.52, 4.00  m is 3 volts. What is the approximate value of Ey in this region? Include the appropriate sign.
Answer:
150 V/m
|
|
 |
 |
 |
|
|
|
|
 |
| Copyright © 2011 John Wiley & Sons, Inc. All rights reserved. |
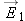 at a location, to find the electric force on whatever particle happens to be at that location, we simply multiply
at a location, to find the electric force on whatever particle happens to be at that location, we simply multiply  by the charge of the particle, q2:
by the charge of the particle, q2:
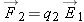
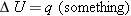
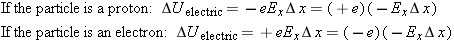


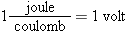
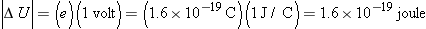
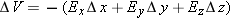
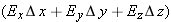 can be written as the “dot product” of the electric field and the displacement vector
can be written as the “dot product” of the electric field and the displacement vector 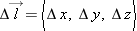 :
:


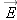 . Conversely, we can calculate electric field from potential difference. Moving in the x direction, we have ΔV = −ExΔx, or
. Conversely, we can calculate electric field from potential difference. Moving in the x direction, we have ΔV = −ExΔx, or
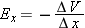
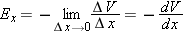


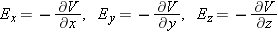
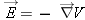 , where the inverted delta (“nabla”) represents taking the x, y, and z partial derivatives of the potential to find the x, y, and z components of the electric field.
, where the inverted delta (“nabla”) represents taking the x, y, and z partial derivatives of the potential to find the x, y, and z components of the electric field.